北京版六年级数学（上册）电子课本可以方便大家随时随地预习或复习课本知识，为此，我们找到了北京版六年级数学（上册）新教材电子书教材的全部内容，以高清图片的形式呈现给大家，希望能够提高大家的学习效率。

如需全套电子课本PDF版，请关注公众号“桃李文库”回复：“电子课本”

北京版六年级数学（上册）新教材电子课本在线阅读（此为截图版，获取是高清版）

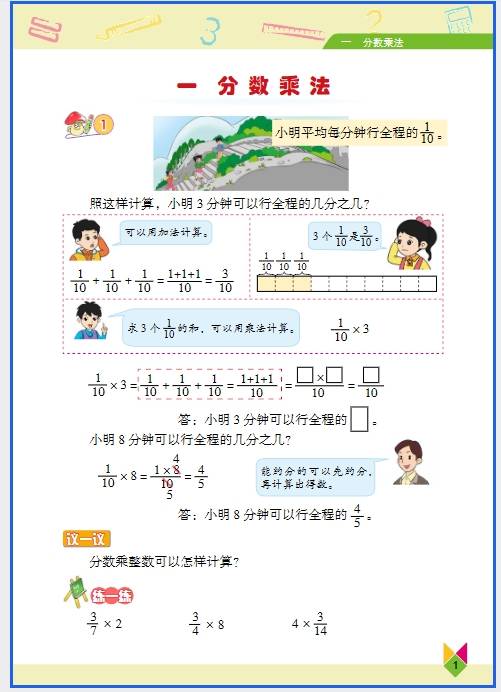
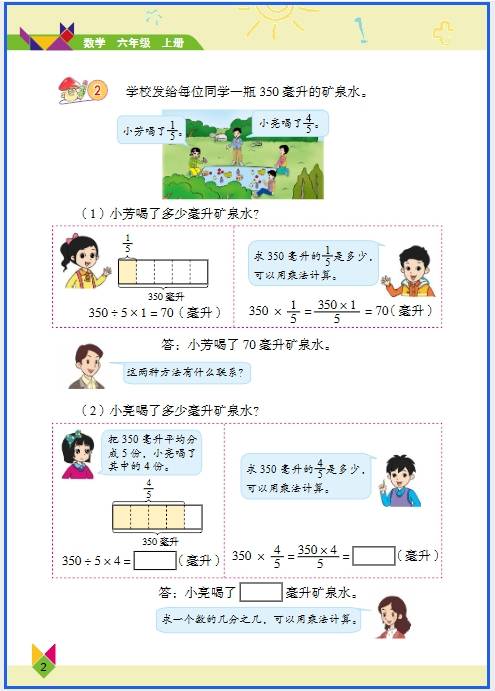
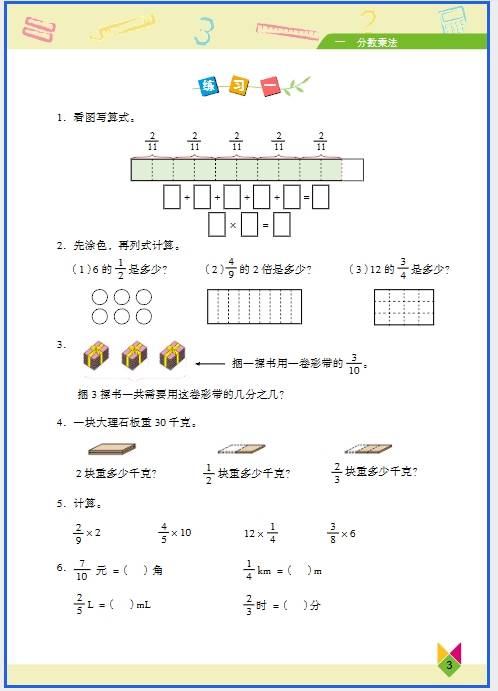
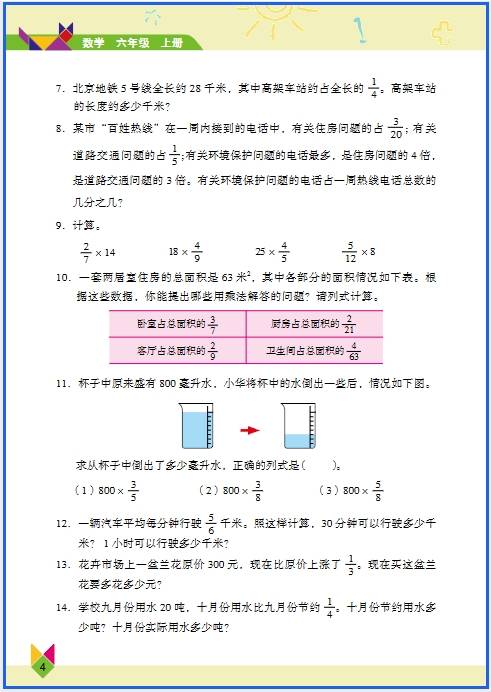
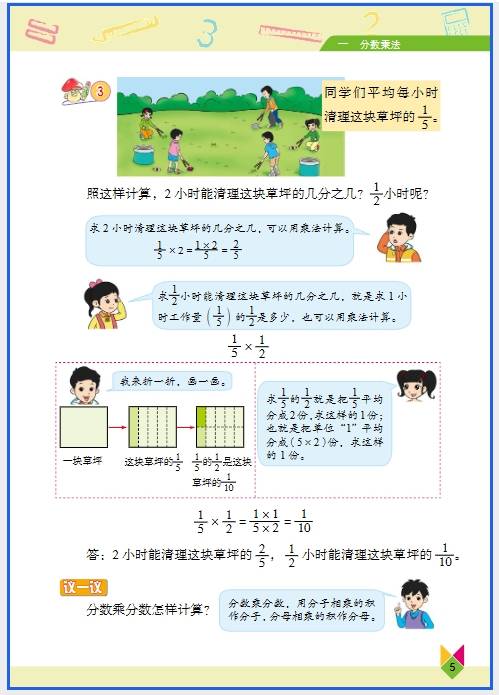
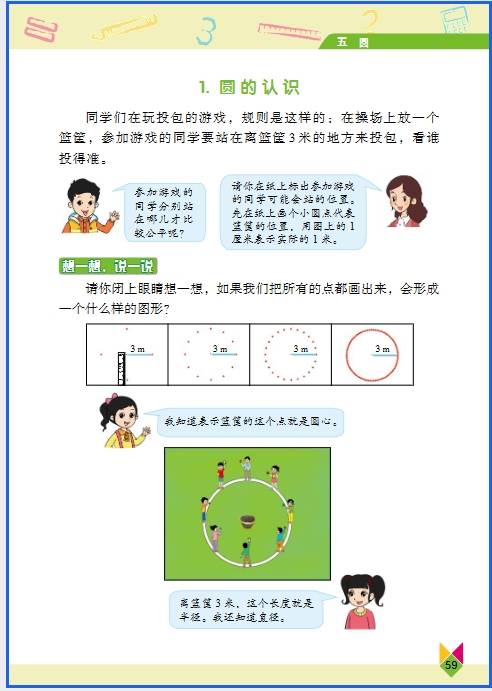
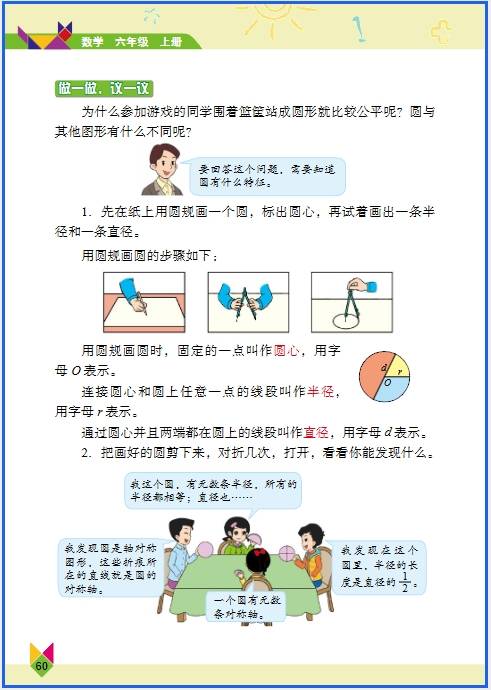
六年级 “数与代数” 的知识看似抽象，其实在生活中处处能用到，从购物算账到规划时间，从理解数据到解决实际问题，都能找到它们的影子。下面结合具体场景，说说常见知识点的应用：

一、整数、小数的运算：生活里的 “基础算账工具”

整数和小数的加减乘除是最常用的，几乎每天都能遇到：

• 购物付款：买东西时算总价、找零。比如买 3 本笔记本，每本 5.8 元，再买一支 2.5 元的笔，总价就是 “3×5.8 + 2.5”，算出来是 19.9 元；如果付了 20 元，找零就是 “20 - 19.9 = 0.1 元”。
• 分物品：家里买了 12 个苹果，分给 4 个人，每人分几个？用 “12÷4 = 3 个”；如果分给 5 个人，每人分 2 个还剩 2 个，对应 “12 = 5×2 + 2”（有余数的除法）。
• 算时间 / 路程：比如步行速度是每分钟 60 米，从家到学校走了 15 分钟，家到学校的距离就是 “60×15 = 900 米”；如果坐公交，2 分钟走了 500 米，公交每分钟走 “500÷2 = 250 米”。

二、分数：解决 “部分与整体” 的问题

分数的核心是 “分率” 和 “具体量”，生活中很多 “分配”“比较” 的场景会用到：

• 分食物 / 资源：一块蛋糕平均分成 8 块，吃了 3 块，就是吃了这块蛋糕的 “3/8”；如果 4 个人分一袋 2 千克的糖果，每人分 “2÷4 = 0.5 千克”，也就是 “1/2 千克”，每人分到的是整袋糖果的 “1/4”（这里要区分 “具体重量” 和 “分率”）。
• 算比例关系：比如调制一杯蜂蜜水，蜂蜜和水的质量比是 1:9，要调 500 克蜂蜜水，需要多少蜂蜜？总份数是 1+9=10 份，蜂蜜占 1/10，所以蜂蜜需要 “500×1/10 = 50 克”，水需要 “500×9/10 = 450 克”。
• 打折优惠：商店搞活动，“八折” 就是按原价的 8/10（或 4/5）出售。一件原价 150 元的衣服，打八折后价格是 “150×8/10 = 120 元”；如果是 “七五折”，就是按原价的 3/4 算，150×3/4=112.5 元。

三、百分数：生活中的 “率” 与 “比较”

百分数和分数类似，但更侧重 “比例的直观表达”，常见于概率、浓度、增长率等场景：

• 折扣与税率：除了上面的 “打折”，百分数还能表示税率。比如买一件 200 元的商品，增值税率是 13%，需要交的税就是 “200×13% = 26 元”，总共要付 “200+26=226 元”。
• 浓度问题：比如一杯盐水，盐有 5 克，水有 45 克，盐水总质量是 50 克，盐占盐水的百分比（浓度）是 “5÷50×100% = 10%”；如果想让浓度变成 20%，再加多少盐？假设加 x 克盐，此时盐有（5+x）克，盐水有（50+x）克，列方程 “（5+x）÷（50+x）=20%”，解得 x=6.25 克（这里也用到了方程思想）。
• 增长率 / 降幅：比如去年家里年收入是 10 万元，今年是 12 万元，今年比去年增长了 “（12-10）÷10×100% = 20%”；如果一件商品原价 200 元，现在降到 160 元，降幅是 “（200-160）÷200×100% = 20%”。
• 概率问题：抛硬币时，正面朝上的概率是 50%；一个袋子里有 3 个红球、2 个白球，摸到红球的概率是 “3÷（3+2）×100% = 60%”。

四、比和比例：解决 “对应关系” 的问题

比和比例的核心是 “两个量的对应倍数关系”，常用来做 “按比例分配”“缩放”“找等量”：

• 按比例分配：比如父母和孩子三人的年龄比是 10:9:3，三人年龄总和是 66 岁，求每人年龄。总份数是 10+9+3=22 份，1 份对应 “66÷22=3 岁”，所以父母年龄分别是 “10×3=30 岁”“9×3=27 岁”，孩子是 “3×3=9 岁”。
• 图形缩放：比如手机照片原尺寸是 “长 12 厘米、宽 9 厘米”，要打印成 “长 8 厘米” 的照片（按比例缩放），宽应该是多少？长的缩放比例是 “8÷12=2/3”，所以宽也要乘 2/3，即 “9×2/3=6 厘米”（对应 “比例的基本性质：两内项之积等于两外项之积”，12:9=8: 宽，12× 宽 = 9×8，宽 = 72÷12=6）。
• 换东西 / 算单价：比如 “2 支笔换 5 块橡皮”，那么 6 支笔能换多少块橡皮？笔的数量从 2 变成 6，乘了 3，所以橡皮也乘 3，“5×3=15 块”（比例关系：2:5=6:15）；再比如 “3 千克苹果 12 元”，算 1 千克苹果多少钱（单价），就是 “12:3=4:1”，即 1 千克 4 元。

五、简易方程：用 “字母” 解决复杂问题

当问题里有 “未知量”，且数量关系明确时，列方程比算术法更简单：

• 求未知量：比如买了 5 本练习本，付了 20 元，找回 2.5 元，求每本练习本多少钱？设每本 x 元，根据 “总价 = 付的钱 - 找回的钱”，列方程 “5x=20-2.5”，解得 “5x=17.5，x=3.5”，即每本 3.5 元。
• 年龄问题：爸爸今年 40 岁，儿子今年 12 岁，几年后爸爸的年龄是儿子的 3 倍？设 x 年后，此时爸爸 40+x 岁，儿子 12+x 岁，列方程 “40+x=3×（12+x）”，解：40+x=36+3x，2x=4，x=2，即 2 年后。
• 行程问题：甲、乙两地相距 300 千米，客车每小时行 60 千米，货车每小时行 40 千米，两车同时从两地出发相向而行，几小时后相遇？设 x 小时后相遇，客车走的路程 + 货车走的路程 = 总路程，列方程 “60x+40x=300”，100x=300，x=3，即 3 小时后相遇。

六、负数：表示 “相反意义的量”

负数用来区分 “正向” 和 “反向” 的量，生活中常见于温度、海拔、记账：

• 温度：天气预报说 “今天最低气温 - 5℃，最高气温 8℃”，“-5℃” 表示零下 5℃，比 0℃低 5℃；8℃是零上 8℃，两者相差 “8 - (-5)=13℃”。
• 海拔：珠穆朗玛峰海拔约 + 8848 米（“+” 可省略），表示比海平面高 8848 米；死海海拔约 - 430 米，表示比海平面低 430 米，两者高度差是 “8848 - (-430)=9278 米”。
• 记账：家里账本上，“+500 元” 表示收入 500 元，“-300 元” 表示支出 300 元；如果月初余额是 2000 元，本月收入 + 1200 元、支出 - 800 元，月末余额是 “2000+1200-800=2400 元”。

其实生活中用到 “数与代数” 的地方远不止这些 —— 比如算水电费（小数运算）、规划零花钱（分数分配）、看手机电量（百分数）、调奶茶的配方（比例）…… 只要多留意，就能发现数学不是课本上的 “题”，而是帮我们把生活变清晰的 “工具” 呢！