华东师大版七年级数学（上册） 电子课本可以方便大家随时随地预习或复习课本知识，为此，我们找到了华东师大版七年级语文（上册） 新教材电子书教材的全部内容，以高清图片的形式呈现给大家，希望能够提高大家的学习效率。

以下是部分内容截图，完整信息请查看 PDF 文件

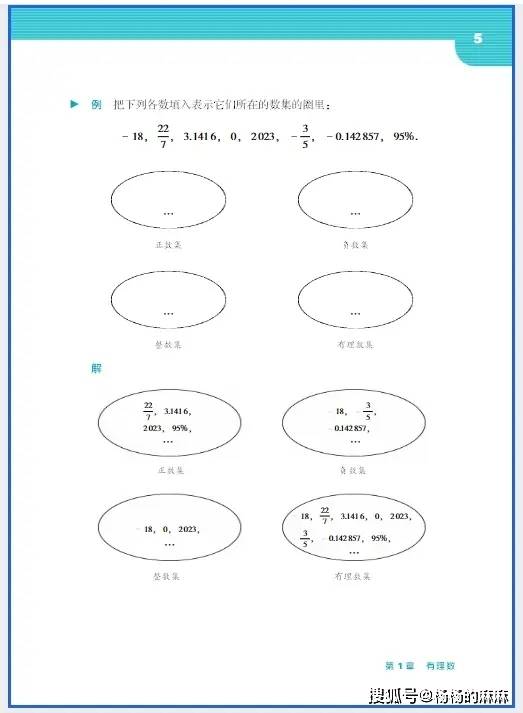
培养七年级学生的数学抽象建模能力，需贴合其 “具体形象思维为主、抽象逻辑思维逐步发展” 的认知特点，遵循 “生活情境引入 — 数学语言转化 — 模型应用验证” 的闭环路径，引导学生逐步掌握 “用数学视角解读问题、用数学方法解决问题” 的能力。以下从核心定位、分阶段策略、避坑指南与工具辅助四方面，提供可落地的培养方案：

一、核心定位：明确七年级抽象建模的 “能力关键点”

七年级数学抽象建模的核心目标是 “将实际问题转化为数学模型并解决”，具体需突破三个能力关键点，培养时需精准发力：

1. 信息提炼能力：从购物、行程、图形操作等具体情境中，剔除无关信息（如问题中的场景描述、冗余数据），聚焦核心 “数量关系”（如总价与单价的关系、路程与速度的关系）或 “图形特征”（如线段的和差、角的互补）；
2. 模型构建能力：将提炼的关系转化为标准化数学模型，如用一元一次方程表示等量关系、用线段图呈现行程问题、用增长率公式描述变化规律；
3. 验证反思能力：用数学方法求解模型后，回归实际问题检验结果合理性（如人数不能为小数、速度不能为负数），避免 “计算正确但脱离实际” 的误区。

二、分阶段培养策略：从 “具象感知” 到 “独立建模” 的进阶路径

阶段 1：具象感知 —— 用生活场景搭建 “抽象桥梁”

七年级学生对抽象模型的理解需依托具体载体，通过生活化、可视化案例，让学生感知 “数学模型源于生活”，消除对 “建模” 的陌生感。

1. 从日常场景提炼数量关系，突破抽象障碍

选取学生熟悉的校园、家庭、运动场景，通过 “阶梯式提问” 引导剥离无关信息，聚焦核心关系：

▶ 案例（校园场景）：抽象 “一元一次方程模型”

问题：“学校组织春游，全班 45 人，租用 3 辆大车和 2 辆小车刚好坐满，每辆大车坐 x 人，每辆小车坐 8 人，求每辆大车坐多少人？”

引导步骤：

① 筛选有用信息：总人数 45 人、3 辆大车、每辆 x 人、2 辆小车、每辆 8 人；

② 梳理数量关系：大车总人数 + 小车总人数 = 全班人数；

③ 转化数学表达：3x + 2×8 = 45。

关键：让学生理解 “x 是未知量，等式是对‘人数关系’的数学翻译”，而非抽象符号。

1. 从动手操作提炼几何模型，强化空间认知

结合七年级几何 “线段、角、三角形” 等知识点，通过动手实践让学生感知 “图形特征与数学表达的关联”：

▶ 案例（图形操作）：抽象 “三角形内角和模型”

让学生用剪刀剪出不同形状的三角形（锐角、直角、钝角三角形），将三个内角剪下拼合，观察是否能组成平角（180°）；再引导用 “平行线的性质” 推导内角和，最终提炼 “三角形内角和为 180°” 的模型。

升级应用：给出问题 “一个三角形两个内角分别为 50° 和 70°，求第三个内角”，让学生用模型快速求解，感受模型的实用性。

阶段 2：框架搭建 —— 掌握 “四步建模法” 形成思维惯性

抽象建模并非无章可循，可将其简化为 “四步流程”，通过典型例题反复强化，让学生形成标准化思维路径：

步骤

核心任务

七年级典型案例（工程问题）

易错点应对策略

1. 审题析量

标注已知量、未知量，梳理关系

已知：师傅每天做 15 个零件，徒弟每天做 x 个，两人合作 5 天完成 140 个；未知：徒弟每天做的数量 x；关系：（师傅效率 + 徒弟效率）× 时间 = 总工作量

用不同符号标注（已知量画横线，未知量画问号），避免遗漏信息

2. 设元列模

设未知数，将关系转化为数学式子

设徒弟每天做 x 个，列方程：(15 + x)×5 = 140

强调 “单位统一”（如天与小时换算），避免单位混淆导致模型错误

3. 求解模型

用代数方法解数学式子

展开方程：75 + 5x = 140→5x = 65→x = 13

要求写出关键步骤，如移项、合并同类项，减少计算失误

4. 验答反思

检验结果是否符合实际，反思合理性

x=13（徒弟每天做 13 个，两人每天共做 28 个，5 天做 140 个，符合总工作量）

强制提问 “结果是否符合生活常识”（如零件数量不能为负数），培养反思习惯

强化训练：针对同一模型设计不同场景题，如 “一元一次方程模型” 可覆盖 “工程问题（零件加工）”“分配问题（文具分发）”“计费问题（手机套餐）”，让学生体会 “不同场景、同一模型”，理解建模的通用性。

阶段 3：灵活进阶 —— 用 “变式与综合题” 打破思维定式

当学生掌握基础建模流程后，通过变式题、综合题提升建模灵活性，避免 “套公式” 的机械思维。

1. 变式训练：调整条件或提问，提升模型识别能力

▶ 原问题（基础模型）：“一支钢笔 15 元，买 4 支需要多少元？”（模型：总价 = 单价 × 数量）；

▶ 变式 1（逆向求解）：“用 60 元买钢笔，每支 15 元，能买几支？”（模型：数量 = 总价 ÷ 单价）；

▶ 变式 2（增加约束）：“用 60 元买钢笔，每支 15 元，买后剩 15 元，实际买了几支？”（模型：单价 × 数量 + 剩余钱数 = 总钱数）；

▶ 变式 3（结合优惠）：“钢笔原价 15 元，促销买 3 送 1，用 60 元最多能买几支？”（模型：先算原价能买数量，再算赠送数量）。

关键：引导学生对比 “变式与原问题的差异”，明确 “模型需根据条件调整，而非一成不变”。

1. 综合训练：融合代数与几何，培养多模型联动能力

七年级综合题常以 “代数 + 几何” 形式呈现，需引导学生 “拆分问题、分别建模”：

▶ 案例（坐标系与几何结合）：

问题：“在平面直角坐标系中，点 A (2,0)，点 B (0,3)，点 C 在 x 轴上，且△ABC 的面积为 6，求点 C 的坐标。”

建模步骤：

① 几何模型：△ABC 以 AC 为底，OB（B 点纵坐标）为高，面积 = 1/2×AC×OB；

② 代数模型：设 C 点坐标为 (x,0)，则 AC=|x-2|，代入面积公式：1/2×|x-2|×3=6；

③ 求解验证：解得 | x-2|=4→x=6 或 x=-2，对应 C 点坐标 (6,0) 或 (-2,0)，均符合 x 轴上点的特征。

关键：让学生学会 “先处理几何中的面积公式，再转化为代数中的绝对值方程”，实现多模型联动。

阶段 4：实践应用 —— 用真实项目感受建模价值

通过 “校园项目”“生活问题” 让学生体会 “数学建模是解决实际问题的工具”，提升学习动力。

1. 校园实践项目：解决校园中的数学问题

▶ 项目 1：班级活动经费规划

任务：“班级有 300 元活动经费，要购买零食和奖品，零食每份 8 元，奖品每份 15 元，共买 25 份，零食和奖品各买多少份？”

建模：设零食买 x 份，奖品买 (25-x) 份，列方程 8x + 15 (25-x)=300，求解并检验是否符合 “份数为整数” 的实际需求。

▶ 项目 2：操场跑道长度测算

任务：“不用专业工具，如何用卷尺测算操场跑道（由两个半圆和一个长方形组成）的周长？”

建模：将跑道抽象为 “长方形周长 + 圆形周长” 模型，测量长方形的长（直道长度）和宽（半圆直径），代入公式计算。

1. 生活热点关联：用建模解读生活现象

▶ 案例：社区垃圾分类投放点规划

问题：“某社区有 300 户居民，计划设置 2 个垃圾分类投放点，A 投放点服务户数比 B 投放点多 50 户，两个投放点各服务多少户？”

建模：设 B 投放点服务 x 户，A 投放点服务 (x+50) 户，列方程 x + (x+50)=300，求解后讨论 “是否需要根据居民分布调整户数”，让学生感受数学在 “公共服务规划” 中的应用。

三、避坑指南：七年级建模培养的常见误区与解决方法

1. 误区 1：直接灌输模型公式，跳过具象感知

如直接告诉学生 “追及问题公式：速度差 × 时间 = 路程差”，不引导画线段图理解。

解决：坚持 “先体验、再总结”，讲 “利润问题” 前，让学生模拟 “进货 - 定价 - 销售” 过程（如用 10 元买文具，15 元卖出，计算利润），再提炼 “利润 = 售价 - 成本” 公式。

1. 误区 2：侧重解方程训练，忽视审题建模

学生能熟练解 2x-7=15，却无法将 “行程问题” 转化为该方程。

解决：设计 “审题专项训练”，给出 10 个实际问题，不要求求解，仅需写出 “未知量设元” 和 “等量关系”，强化 “从问题到模型” 的转化能力。

1. 误区 3：忽视验答环节，只关注计算结果

如解 “桌椅配套问题” 得到 x=4.2，学生未发现 “桌椅数量不能为小数”。

解决：建立 “验答三问” 机制：① 结果是否符合实际场景？② 代入原问题是否成立？③ 若条件变化，结果会如何调整？强制学生反思结果合理性。

四、工具辅助：降低抽象难度的 “可视化工具”

七年级学生可借助简单工具提升建模效率与兴趣：

1. 几何可视化工具：GeoGebra（动态演示图形运动，如三角形三边关系验证）、实物模型（小棒、立方体，用于拼搭几何图形，理解图形特征）；
2. 数据整理工具：腾讯文档表格（记录多组数据，如 “不同折扣下的商品价格”，直观呈现数量关系）；
3. 思维梳理工具：手绘线段图（梳理行程问题中的路程关系）、思维导图（整理 “一元一次方程模型” 的适用场景，如购物、工程、行程）。

总结

七年级数学抽象建模能力的培养，需遵循 “循序渐进、贴合认知” 的原则：从生活场景中感知模型，用标准化步骤搭建模型，通过变式与综合题灵活运用模型，最终在实际项目中检验模型价值。过程中需包容学生的 “试错”，重点关注 “能否从问题中提炼关系、构建模型”，而非 “能否快速得出正确答案”。唯有让学生真正理解 “建模是解决实际问题的思维方式”，才能为后续八年级函数建模、九年级几何综合建模奠定坚实基础，实现数学思维的深度提升。