人教版六年级数学（上下册）电子课本可以方便大家随时随地预习或复习课本知识，为此，我们找到了人教版六年级数学（上下册）新教材电子书教材的全部内容，以高清图片的形式呈现给大家，希望能够提高大家的学习效率。

如需全套电子课本PDF版，请关注公众号“桃李百科”回复：“电子课本”

人教版六年级数学（上下册）新教材电子课本在线阅读（此为截图版，获取是高清版）

六年级上册

1. 第一单元：分数乘法

• 知识要点：理解分数乘法的意义，分数乘整数表示求几个相同分数的和的简便运算，如\(\frac{2}{3}×5\)表示 5 个\(\frac{2}{3}\)相加；分数乘分数表示求一个分数的几分之几是多少，如\(\frac{2}{3}×\frac{1}{4}\)表示求\(\frac{2}{3}\)的\(\frac{1}{4}\)是多少。掌握分数乘法的计算方法，分子相乘的积作分子，分母相乘的积作分母，能约分的先约分。如\(\frac{3}{4}×\frac{2}{5}=\frac{3×2}{4×5}=\frac{3}{10}\)。
• 应用拓展：学会运用分数乘法解决实际问题，如求一个数的几分之几是多少，已知一个数比另一个数多（或少）几分之几，求这个数等。例如，小明有 20 本书，小红的书比小明多\(\frac{1}{4}\)，则小红有书\(20×(1+\frac{1}{4}) = 20×\frac{5}{4}=25\)本。

1. 第二单元：位置与方向（二）

• 知识要点：能根据方向和距离确定物体的位置，例如，“学校在小明家北偏东 30° 方向，距离 500 米处”。要明确方向角的含义，北偏东 30° 就是以正北方向为起始边，向东旋转 30° 所指的方向。掌握描述路线图的方法，要清楚每一段路的方向和距离。
• 应用拓展：在实际生活中，可用于绘制地图、描述行走路线等。如根据给定的信息，绘制从家到公园的路线图，依次说明每一段路的方向和距离变化。

1. 第三单元：分数除法

• 知识要点：理解分数除法的意义，与整数除法意义相同，已知两个因数的积与其中一个因数，求另一个因数的运算。如已知\(\frac{2}{3}×x=\frac{4}{5}\)，求\(x\)，用除法\(x=\frac{4}{5}÷\frac{2}{3}\)。掌握分数除法的计算方法，除以一个数（0 除外）等于乘这个数的倒数，如\(\frac{4}{5}÷\frac{2}{3}=\frac{4}{5}×\frac{3}{2}=\frac{6}{5}\)。
• 应用拓展：能解决分数除法相关的实际问题，如已知一个数的几分之几是多少，求这个数；已知比一个数多（或少）几分之几的数是多少，求这个数等。例如，小红有 25 本书，是小明书数量的\(\frac{5}{4}\)，则小明有书\(25÷\frac{5}{4}=25×\frac{4}{5}=20\)本。

1. 第四单元：比

• 知识要点：理解比的意义，两个数相除又叫做两个数的比，如\(3÷2\)可写成\(3:2\)，比的前项除以后项所得的商叫做比值，\(3:2\)的比值是\(\frac{3}{2}\)。掌握比的基本性质，比的前项和后项同时乘或除以相同的数（0 除外），比值不变，利用此性质可进行比的化简，如\(6:8=(6÷2):(8÷2)=3:4\)。
• 应用拓展：会运用比解决按比例分配问题，例如，一个三角形三个内角的度数比是\(1:2:3\)，内角和是 180°，则三个角分别为\(180°×\frac{1}{1 + 2 + 3}=30°\)，\(180°×\frac{2}{1 + 2 + 3}=60°\)，\(180°×\frac{3}{1 + 2 + 3}=90°\)。

1. 第五单元：圆

• 知识要点：认识圆的特征，圆心确定圆的位置，半径确定圆的大小，同一圆内所有半径都相等，所有直径也都相等，直径是半径的 2 倍，即\(d = 2r\)。掌握圆的周长公式\(C = πd\)或\(C = 2πr\)（\(C\)表示周长，\(d\)表示直径，\(r\)表示半径，\(π\)通常取 3.14），以及圆的面积公式\(S = πr²\)。如半径为 2 厘米的圆，周长\(C = 2×3.14×2 = 12.56\)厘米，面积\(S = 3.14×2² = 12.56\)平方厘米。
• 应用拓展：能解决与圆相关的实际问题，如求圆形花坛的周长和面积、环形面积（\(S_{环}=π(R² - r²)\)，\(R\)为外圆半径，\(r\)为内圆半径）等。如一个环形，外圆半径 5 厘米，内圆半径 3 厘米，环形面积为\(3.14×(5² - 3²)=3.14×(25 - 9)=50.24\)平方厘米。

1. 第六单元：百分数（一）

• 知识要点：理解百分数的意义，百分数表示一个数是另一个数的百分之几，也叫百分率或百分比，如\(45\%\)表示一个数占另一个数的\(\frac{45}{100}\)。掌握百分数与小数、分数的互化方法，百分数化小数，去掉百分号，小数点向左移动两位，如\(45\% = 0.45\)；小数化百分数，小数点向右移动两位，加上百分号，如\(0.3 = 30\%\)。百分数化分数，先写成分母是 100 的分数，再化简，如\(45\%=\frac{45}{100}=\frac{9}{20}\)；分数化百分数，先把分数化成小数（除不尽时，通常保留三位小数），再化成百分数，如\(\frac{3}{4}=0.75 = 75\%\)。
• 应用拓展：能解决百分数相关的实际问题，如求一个数是另一个数的百分之几、求一个数的百分之几是多少、求比一个数多（或少）百分之几的数是多少等。例如，某班有 50 人，今天出勤 48 人，出勤率为\(48÷50×100\% = 96\%\)。

1. 第七单元：扇形统计图

• 知识要点：认识扇形统计图的特点，它可以清楚地反映出各部分数量与总数量之间的关系。例如，通过扇形统计图能直观看出各类图书在图书馆藏书总量中所占的比例。学会根据扇形统计图提供的信息进行简单的分析和计算，如已知总数量和各部分所占百分比，求各部分数量。
• 应用拓展：在生活中，可用于分析各种统计数据，如分析家庭各项支出占总支出的比例，从而合理规划家庭财务。

1. 第八单元：数学广角 —— 数与形

• 知识要点：体会数与形的密切联系，通过图形直观地理解数学规律，如通过观察正方形点阵图，发现从 1 开始连续奇数的和等于奇数个数的平方，\(1 + 3 + 5 + 7 = 4²\)。利用数形结合的方法解决问题，使复杂的问题简单化，抽象的问题具体化。
• 应用拓展：在解决一些数学问题时，借助图形帮助理解题意，找到解题思路，如计算\(1 + \frac{1}{2}+\frac{1}{4}+\frac{1}{8}+\cdots\)，通过画图可发现其和无限接近于 2。

六年级下册

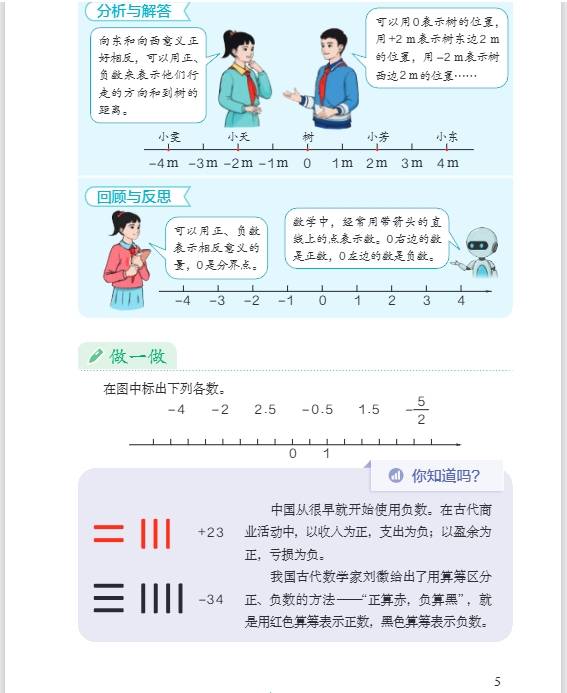
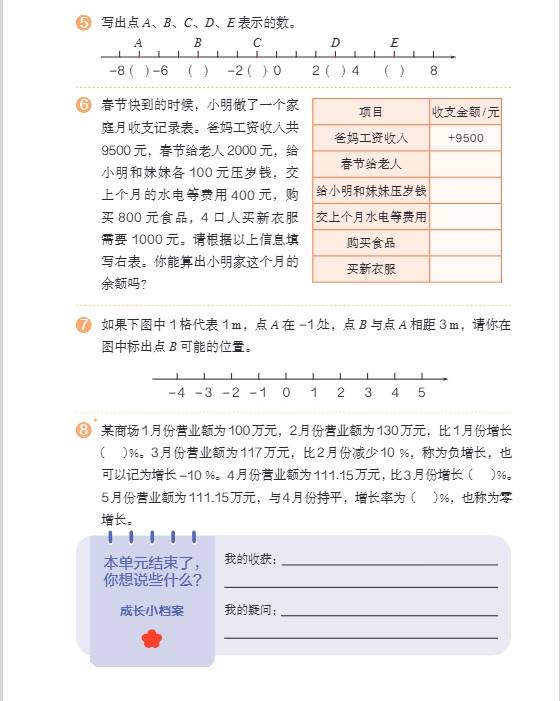
1. 第一单元：负数

• 知识要点：了解负数的意义，负数是比 0 小的数，如\(-3\)、\(-0.5\)等。能正确读写负数，读负数时，先读 “负”，再读数，如\(-3\)读作 “负三”；写负数时，先写 “-”，再写数。掌握正负数在生活中的应用，如用正负数表示相反意义的量，气温零上用正数表示，零下用负数表示；海拔高于海平面用正数表示，低于海平面用负数表示等。
• 应用拓展：在实际情境中，能根据正负数的意义解决问题，如根据商店的盈利与亏损情况，用正负数记录账目。

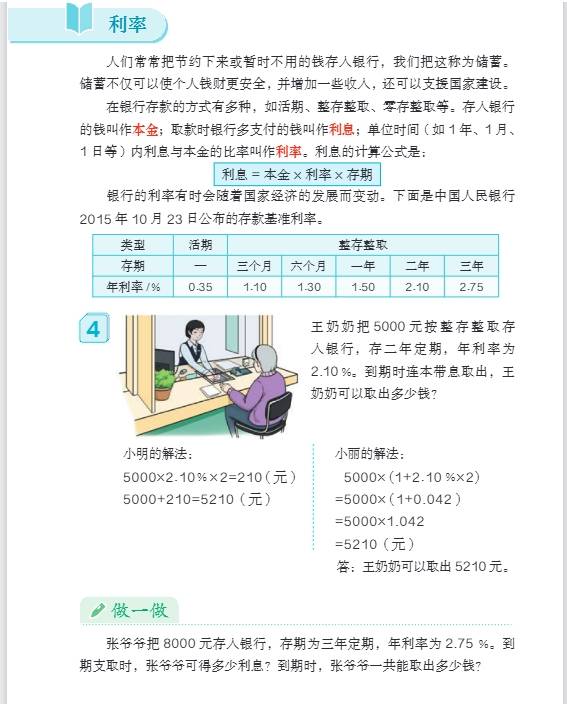
1. 第二单元：百分数（二）

• 知识要点：进一步理解百分数在生活中的应用，如折扣、成数、税率、利率等。折扣表示现价是原价的百分之几，几折就是十分之几，也就是百分之几十，如八折就是\(80\%\)，一件商品原价 100 元，打八折后的价格是\(100×80\% = 80\)元。成数表示一个数是另一个数的十分之几，几成就是十分之几，如三成五就是\(\frac{3.5}{10}=35\%\)。税率是应纳税额与各种收入的比率，利率是利息与本金的比率，掌握利息的计算方法，利息 = 本金 × 利率 × 存期。
• 应用拓展：能解决与折扣、成数、税率、利率等相关的实际问题，如计算商品打折后的价格、缴纳税款的金额、存款到期后的利息等。例如，妈妈存入银行 20000 元，定期三年，年利率是 2.75%，到期后可得利息\(20000×2.75\%×3 = 1650\)元。

1. 第三单元：圆柱与圆锥

• 知识要点：认识圆柱和圆锥的特征，圆柱有两个底面，是完全相同的圆，侧面是一个曲面，展开后是一个长方形（或正方形），圆柱的高有无数条；圆锥有一个底面，是一个圆，侧面是一个曲面，展开后是一个扇形，圆锥只有一条高。掌握圆柱的表面积公式\(S = 2πr² + 2πrh\)（\(S\)为表面积，\(r\)为底面半径，\(h\)为高），体积公式\(V = πr²h\)；圆锥的体积公式\(V=\frac{1}{3}πr²h\)。如一个圆柱底面半径是 2 厘米，高是 5 厘米，表面积为\(2×3.14×2² + 2×3.14×2×5 = 87.92\)平方厘米，体积为\(3.14×2²×5 = 62.8\)立方厘米；一个圆锥底面半径是 3 厘米，高是 4 厘米，体积为\(\frac{1}{3}×3.14×3²×4 = 37.68\)立方厘米。
• 应用拓展：能运用圆柱和圆锥的知识解决实际问题，如求圆柱形水桶的容积、圆锥形沙堆的体积等。如用铁皮制作一个无盖的圆柱形水桶，底面直径 4 分米，高 5 分米，需要铁皮的面积为\(3.14×(4÷2)² + 3.14×4×5 = 75.36\)平方分米，水桶容积为\(3.14×(4÷2)²×5 = 62.8\)立方分米。

1. 第四单元：比例

• 知识要点：理解比例的意义，表示两个比相等的式子叫做比例，如\(2:3 = 4:6\)。掌握比例的基本性质，在比例里，两个外项的积等于两个内项的积，如在\(2:3 = 4:6\)中，\(2×6 = 3×4\)。会解比例，根据比例的基本性质，已知比例中的任何三项，就可以求出这个比例中的另外一个未知项。如\(3:x = 6:8\)，则\(6x = 3×8\)，\(x = 4\)。认识正比例和反比例关系，两种相关联的量，一种量变化，另一种量也随着变化，如果这两种量中相对应的两个数的比值一定，这两种量就叫做成正比例的量，它们的关系叫做正比例关系，如路程 ÷ 时间 = 速度（一定），路程与时间成正比例；如果这两种量中相对应的两个数的乘积一定，这两种量就叫做成反比例的量，它们的关系叫做反比例关系，如长 × 宽 = 面积（一定），长与宽成反比例。
• 应用拓展：能运用比例知识解决实际问题，如比例尺问题，图上距离：实际距离 = 比例尺，已知比例尺和图上距离可求实际距离，已知比例尺和实际距离可求图上距离。例如，在一幅比例尺是 1:5000000 的地图上，量得甲、乙两地的距离是 3 厘米，那么甲、乙两地的实际距离是\(3×5000000 = 15000000\)厘米 = 150 千米。

1. 第五单元：数学广角 —— 鸽巢问题

• 知识要点：理解鸽巢原理，把\(n + 1\)个物体放进\(n\)个抽屉里，总有一个抽屉里至少放 2 个物体；把\(m×n + 1\)个物体放进\(n\)个抽屉里，总有一个抽屉里至少放\((m + 1)\)个物体。例如，把 5 个苹果放进 4 个抽屉，总有一个抽屉至少放 2 个苹果；把 11 个苹果放进 4 个抽屉，\(11÷4 = 2\cdots\cdots3\)，总有一个抽屉至少放\(2 + 1 = 3\)个苹果。
• 应用拓展：能运用鸽巢原理解决实际问题，如在任意 367 个人中，至少有 2 个人的生日在同一天；从一副扑克牌（去掉大小王）中任意抽取 14 张牌，至少有 2 张牌的花色相同。

1. 第六单元：整理和复习

• 知识要点：对小学阶段所学的数学知识进行系统整理和复习，包括数与代数、图形与几何、统计与概率、综合与实践等领域。在数与代数方面，复习整数、小数、分数、百分数、负数等数的认识和运算，方程、比和比例等知识；在图形与几何方面，复习平面图形和立体图形的特征、周长、面积、体积等计算；在统计与概率方面，复习统计图表的认识和应用，可能性的知识；在综合与实践方面，回顾解决问题的策略和方法，提高综合运用知识解决实际问题的能力。
• 应用拓展：通过综合练习和实际问题的解决，巩固所学知识，提高解题能力和思维水平，培养创新意识和实践能力，为初中数学学习奠定基础。例如，通过解决实际生活中的工程问题、行程问题等，综合运用数学知识，提高分析问题和解决问题的能力。