北京版五年级数学（下册）电子课本可以方便大家随时随地预习或复习课本知识，为此，我们找到了北京版五年级数学（下册）新教材电子书教材的全部内容，以高清图片的形式呈现给大家，希望能够提高大家的学习效率。

如需全套电子课本PDF版，请关注公众号“桃李百科”回复：“电子课本”

北京版五年级数学（下册）新教材电子课本在线阅读（此为截图版，获取是高清版）

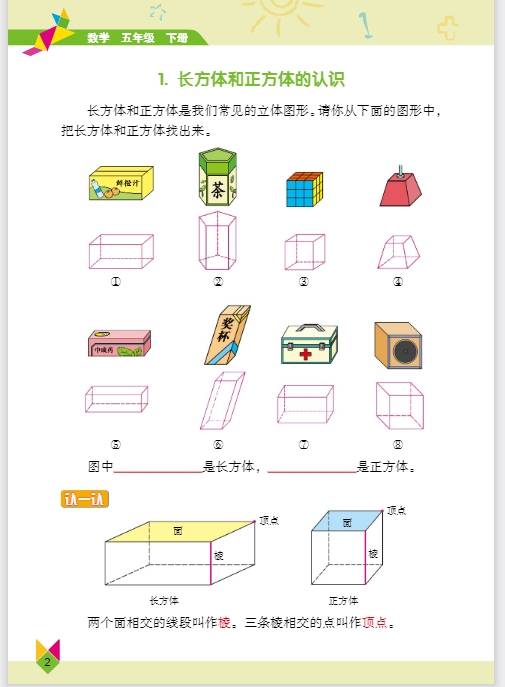
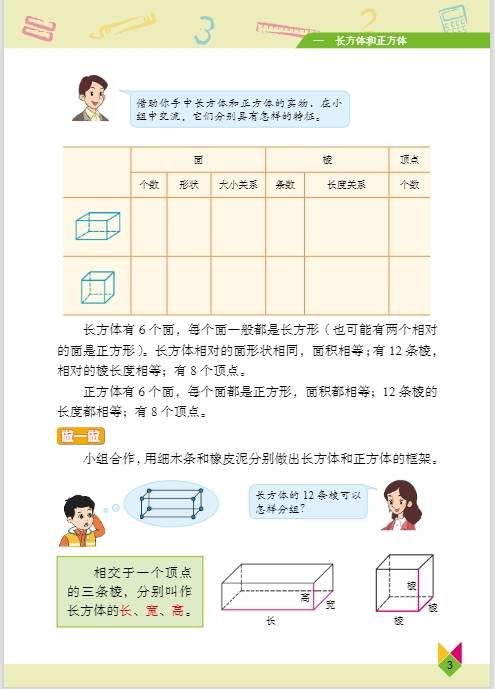
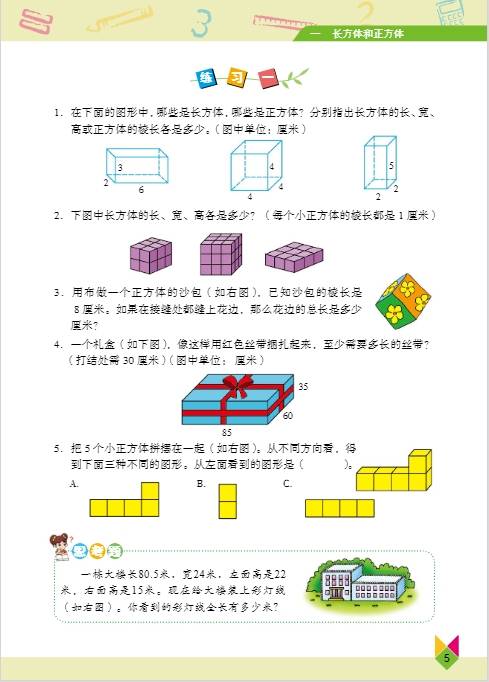
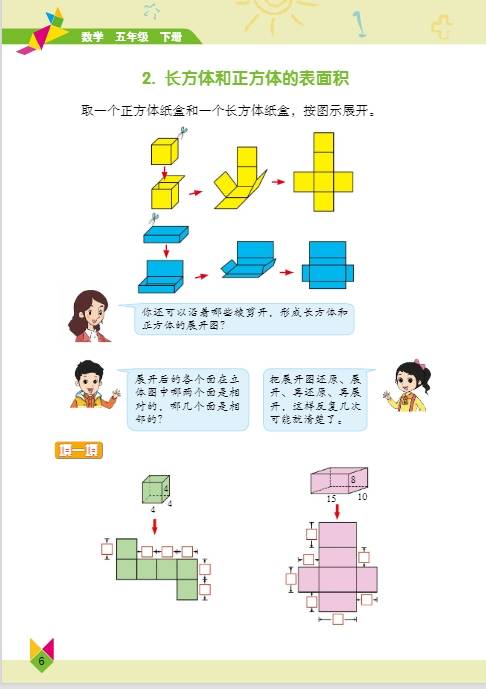
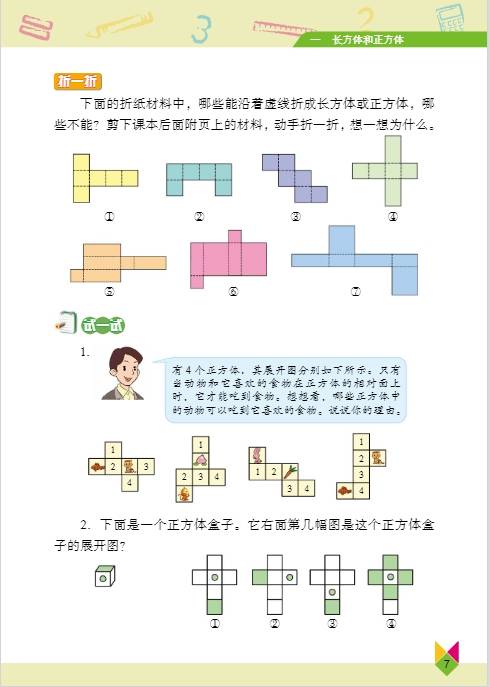
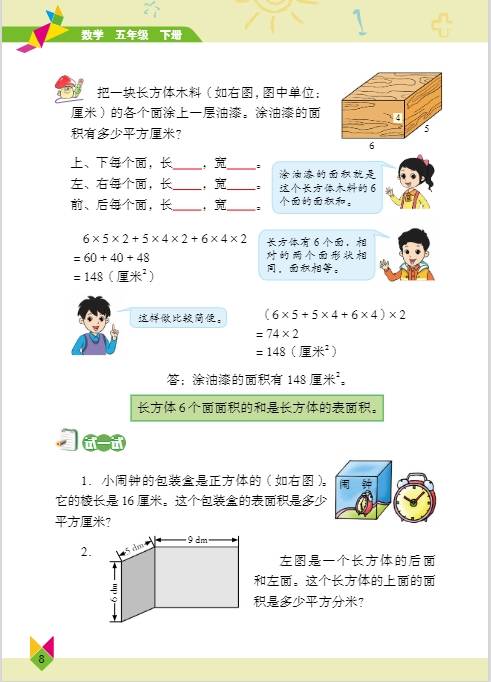
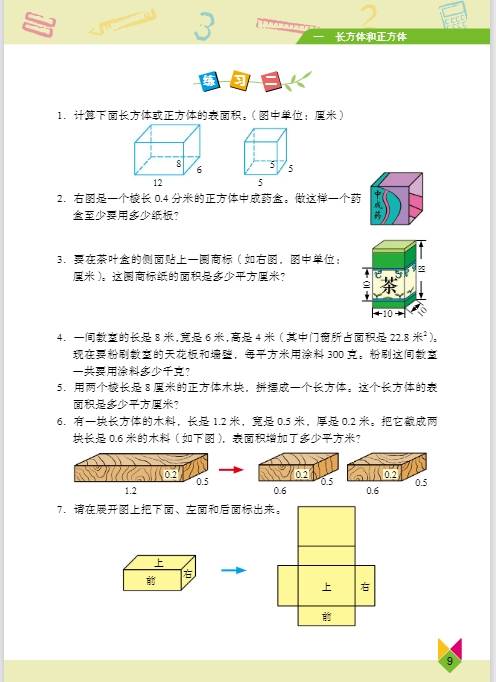
第一单元：长方体和正方体

• 知识要点：学生要认识长方体和正方体的基本特征，长方体有 6 个面，相对的面完全相同；12 条棱，相对的棱长度相等；8 个顶点。正方体是特殊的长方体，它的 6 个面都是正方形，12 条棱长度都相等。掌握长方体和正方体表面积的计算方法，长方体表面积 =（长 × 宽 + 长 × 高 + 宽 × 高）×2 ，正方体表面积 = 棱长 × 棱长 ×6 。理解体积和容积的概念，体积是物体所占空间的大小，容积是容器所能容纳物体的体积，常用体积单位有立方米、立方分米、立方厘米，容积单位有升、毫升，1 升 = 1 立方分米，1 毫升 = 1 立方厘米 ，学会计算长方体和正方体的体积，长方体体积 = 长 × 宽 × 高 ，正方体体积 = 棱长 × 棱长 × 棱长 ，也可统一为体积 = 底面积 × 高 。
• 重点难点：重点是理解长方体和正方体的特征、表面积、体积和容积的概念及计算方法。难点是根据实际问题灵活运用公式，确定所求的是几个面的面积，以及理解体积和容积的区别与联系 。
• 学习成果：学生能够运用所学知识解决生活中与长方体和正方体相关的实际问题，如计算物体的包装材料面积、容器的容积等，增强空间观念和解决实际问题的能力，体会数学在生活中的广泛应用 。

第二单元：折线统计图与可能性

• 知识要点：认识折线统计图，了解其特点是能清晰地反映数据的变化趋势。学会绘制单式和复式折线统计图，能根据折线统计图中的数据进行分析、预测和决策 。了解事件发生的可能性，知道事件发生的可能性有大小之分，能对简单事件发生的可能性进行描述和判断 。
• 重点难点：重点是掌握折线统计图的绘制和分析方法，理解事件发生可能性的大小 。难点是根据折线统计图中的数据进行合理预测，以及准确判断复杂事件发生的可能性 。
• 学习成果：学生能够用折线统计图描述和分析数据，培养数据分析观念和统计意识，能对生活中的事件发生的可能性进行判断和分析，提高解决实际问题的能力 。

第三单元：分数的意义和性质

• 知识要点：理解分数的意义，把单位 “1” 平均分成若干份，表示这样一份或几份的数叫分数，明确分数单位的概念 。掌握分数与除法的关系，被除数相当于分子，除数相当于分母 。认识真分数、假分数和带分数，学会假分数与带分数或整数的互化 。理解分数的基本性质，分数的分子和分母同时乘或除以相同的数（0 除外），分数的大小不变 ，会根据分数的基本性质进行约分和通分，比较分数的大小 。
• 重点难点：重点是分数的意义、基本性质，以及约分和通分 。难点是理解分数的意义和分数基本性质的推导过程，在实际应用中灵活运用分数知识解决问题 。
• 学习成果：学生建立起分数的概念体系，能够运用分数知识解决生活中的问题，如分物品、计算比例等，提高数感和运算能力，培养数学思维和逻辑推理能力 。

第四单元：分数加法和减法

• 知识要点：掌握同分母分数加减法的计算方法，分母不变，分子相加减 。学会异分母分数加减法，先通分转化为同分母分数，再按同分母分数加减法计算 。了解分数加减混合运算的顺序，与整数加减混合运算顺序相同 ，整数加法的交换律和结合律在分数加法中同样适用，能运用运算定律进行简便运算 。
• 重点难点：重点是分数加减法的计算方法 。难点是理解异分母分数加减法的算理，以及在计算过程中正确进行通分和约分 。
• 学习成果：学生能够熟练进行分数的加减法运算，提高运算能力和解决实际问题的能力，体会数学知识之间的内在联系和运算的一致性 。

第五单元：方程

• 知识要点：理解方程的意义，含有未知数的等式叫方程 。掌握等式的性质，等式两边同时加上或减去同一个数，等式仍然成立；等式两边同时乘或除以同一个不为 0 的数，等式仍然成立 。学会用方程表示简单情境中的等量关系，能根据等式的性质解方程 ，并能运用方程解决一些简单的实际问题 。
• 重点难点：重点是方程的意义、等式的性质和用方程解决实际问题 。难点是找出实际问题中的等量关系，正确列出方程并求解 。
• 学习成果：学生能够运用方程解决生活中的实际问题，如行程问题、工程问题等，体会方程在解决问题中的优势，提高分析问题和解决问题的能力，培养代数思维 。

第六单元：数学百花园

• 知识要点：通过本单元学习，接触一些有趣的数学问题和数学思想方法，如 “鸡兔同笼” 问题，学习用假设法、列表法等方法解决问题 。了解 “密铺” 现象，知道哪些图形可以密铺，以及密铺的原理 。
• 重点难点：重点是掌握解决 “鸡兔同笼” 等问题的方法，理解密铺的原理 。难点是在实际问题中灵活运用所学方法，以及对复杂密铺问题的分析和判断 。
• 学习成果：学生提高逻辑思维能力和推理能力，学会运用数学方法解决实际问题，培养创新意识和实践能力，感受数学的趣味性和实用性 。