北京版八年级数学（下册）电子课本可以方便大家随时随地预习或复习课本知识，为此，我们找到了北京版八年级数学（下册）新教材电子书教材的全部内容，以高清图片的形式呈现给大家，希望能够提高大家的学习效率。

如需全套电子课本PDF版，请关注公众号“桃李百科”回复：“电子课本”

北京版八年级数学（下册）新教材电子课本在线阅读（此为截图版，获取是高清版）

2025 新教材人教版八年级数学（下册）单元知识点总结

第十六章：二次根式

二次根式的概念

1. 定义：一般地，形如\(\sqrt{a}\)（\(a\geqslant0\)）的式子叫做二次根式。其中，\(a\)是被开方数，“\(\sqrt{}\)” 称为二次根号。例如，\(\sqrt{4}\)，\(\sqrt{x^2 + 1}\)（\(x\)为任意实数时，\(x^2 + 1\geqslant1\gt0\)）等都是二次根式；而\(\sqrt{-2}\)，因为被开方数\(-2\lt0\)，所以它不是二次根式。
2. 有意义的条件：被开方数\(a\geqslant0\)。这是因为在实数范围内，负数没有平方根。比如，要使\(\sqrt{x - 3}\)有意义，则\(x - 3\geqslant0\)，即\(x\geqslant3\)。

二次根式的性质

1. \((\sqrt{a})^2 = a\)（\(a\geqslant0\)）：例如\((\sqrt{5})^2 = 5\)，\((\sqrt{x^2})^2 = x^2\)（\(x\)为任意实数，因为\(x^2\geqslant0\)）。这一性质表明一个非负数的算术平方根的平方等于它本身。
2. \(\sqrt{a^2} = \vert a\vert\)，当\(a\geqslant0\)时，\(\sqrt{a^2} = a\)；当\(a\lt0\)时，\(\sqrt{a^2} = -a\)：例如，当\(a = 3\)时，\(\sqrt{3^2} = \sqrt{9} = 3\)；当\(a = -3\)时，\(\sqrt{(-3)^2} = \sqrt{9} = 3 = -(-3)\)。该性质体现了二次根式对一个数平方的开方运算与绝对值的关系。

二次根式的运算

1. 乘法法则：\(\sqrt{a}\cdot\sqrt{b} = \sqrt{ab}\)（\(a\geqslant0\)，\(b\geqslant0\)）。例如\(\sqrt{2}\cdot\sqrt{3} = \sqrt{2\times3} = \sqrt{6}\)；\(\sqrt{5x}\cdot\sqrt{10y} = \sqrt{5x\cdot10y} = \sqrt{50xy} = 5\sqrt{2xy}\)（\(x\geqslant0\)，\(y\geqslant0\)）。
2. 除法法则：\(\frac{\sqrt{a}}{\sqrt{b}} = \sqrt{\frac{a}{b}}\)（\(a\geqslant0\)，\(b\gt0\)）。例如\(\frac{\sqrt{8}}{\sqrt{2}} = \sqrt{\frac{8}{2}} = \sqrt{4} = 2\)；\(\frac{\sqrt{12x^3}}{\sqrt{3x}} = \sqrt{\frac{12x^3}{3x}} = \sqrt{4x^2} = 2x\)（\(x\gt0\)）。
3. 加减法：先将二次根式化为最简二次根式，再将被开方数相同的二次根式进行合并。例如，计算\(\sqrt{12} + \sqrt{27} - \sqrt{48}\)，先化简：\(\sqrt{12} = 2\sqrt{3}\)，\(\sqrt{27} = 3\sqrt{3}\)，\(\sqrt{48} = 4\sqrt{3}\)，然后合并：\(2\sqrt{3} + 3\sqrt{3} - 4\sqrt{3} = (2 + 3 - 4)\sqrt{3} = \sqrt{3}\)。
4. 混合运算：与实数的混合运算顺序相同，先乘方，再乘除，最后加减，有括号的先算括号里面的。例如计算\((\sqrt{3} + 1)^2 - \sqrt{12}\div\sqrt{3}\)，先算乘方：\((\sqrt{3} + 1)^2 = (\sqrt{3})^2 + 2\sqrt{3} + 1^2 = 3 + 2\sqrt{3} + 1 = 4 + 2\sqrt{3}\)，再算除法：\(\sqrt{12}\div\sqrt{3} = \sqrt{4} = 2\)，最后相减：\((4 + 2\sqrt{3}) - 2 = 2 + 2\sqrt{3}\)。

第十七章：勾股定理

勾股定理

1. 内容：如果直角三角形的两直角边长分别为\(a\)，\(b\)，斜边长为\(c\)，那么\(a^2 + b^2 = c^2\)。例如，在一个直角三角形中，两直角边分别为\(3\)和\(4\)，根据勾股定理，斜边\(c = \sqrt{3^2 + 4^2} = \sqrt{9 + 16} = \sqrt{25} = 5\)。
2. 证明方法：常见的有赵爽弦图法、毕达哥拉斯证法等。以赵爽弦图为例，通过四个全等的直角三角形与中间小正方形拼成一个大正方形，利用大正方形面积等于四个直角三角形面积与小正方形面积之和来证明勾股定理。设直角三角形的直角边分别为\(a\)、\(b\)，斜边为\(c\)，大正方形边长为\(a + b\)，其面积为\((a + b)^2\)，四个直角三角形面积为\(4\times\frac{1}{2}ab\)，小正方形边长为\(b - a\)（假设\(b\gt a\)），面积为\((b - a)^2\)，则\((a + b)^2 = 4\times\frac{1}{2}ab + (b - a)^2\)，展开化简可得\(a^2 + b^2 = c^2\)。

勾股定理的逆定理

1. 内容：如果三角形的三边长\(a\)，\(b\)，\(c\)满足\(a^2 + b^2 = c^2\)，那么这个三角形是直角三角形。例如，已知三角形三边分别为\(5\)，\(12\)，\(13\)，因为\(5^2 + 12^2 = 25 + 144 = 169 = 13^2\)，所以这个三角形是直角三角形。
2. 应用：用于判断一个三角形是否为直角三角形，在实际生活中，如测量土地、建筑施工等方面可用于确定直角。比如，在一块空地上要确定一个直角区域，可先测量出三条边的长度，通过勾股定理的逆定理来验证是否构成直角。

勾股定理的应用

1. 解决实际问题：例如，一个门框的尺寸是高\(2m\)，宽\(1m\)，一块长\(3m\)，宽\(2.2m\)的长方形薄木板能否从门框内通过？可以将门框的对角线看作直角三角形的斜边，根据勾股定理，对角线长为\(\sqrt{2^2 + 1^2} = \sqrt{4 + 1} = \sqrt{5}\approx2.24m\)，因为\(2.24\gt2.2\)，所以木板能通过。
2. 在几何图形中的应用：在正方形、矩形、菱形等几何图形中，常利用勾股定理求边长、对角线长等。如在菱形\(ABCD\)中，对角线\(AC = 6\)，\(BD = 8\)，因为菱形对角线互相垂直平分，设对角线交点为\(O\)，则\(AO = 3\)，\(BO = 4\)，在直角三角形\(ABO\)中，根据勾股定理可得边长\(AB = \sqrt{3^2 + 4^2} = 5\)。

第十八章：平行四边形

平行四边形

1. 定义：两组对边分别平行的四边形叫做平行四边形。用符号 “\(\parallelogram\)” 表示，如平行四边形\(ABCD\)记作 “\(\parallelogram ABCD\)”。
2. 性质

• 边：平行四边形的对边平行且相等。即\(AB\parallel CD\)，\(AB = CD\)；\(AD\parallel BC\)，\(AD = BC\)。
• 角：平行四边形的对角相等，邻角互补。\(\angle A = \angle C\)，\(\angle B = \angle D\)；\(\angle A + \angle B = 180^{\circ}\)，\(\angle B + \angle C = 180^{\circ}\)等。
• 对角线：平行四边形的对角线互相平分。即\(OA = OC\)，\(OB = OD\)，其中\(AC\)、\(BD\)为对角线，交点为\(O\)。

1. 判定

• 边：两组对边分别平行的四边形是平行四边形；两组对边分别相等的四边形是平行四边形；一组对边平行且相等的四边形是平行四边形。
• 角：两组对角分别相等的四边形是平行四边形。
• 对角线：对角线互相平分的四边形是平行四边形。

特殊的平行四边形

1. 矩形

• 定义：有一个角是直角的平行四边形叫做矩形。
• 性质：除具有平行四边形的所有性质外，还具有四个角都是直角，对角线相等的性质。即\(\angle A = \angle B = \angle C = \angle D = 90^{\circ}\)，\(AC = BD\)。
• 判定：有一个角是直角的平行四边形是矩形；对角线相等的平行四边形是矩形；有三个角是直角的四边形是矩形。

1. 菱形

• 定义：有一组邻边相等的平行四边形叫做菱形。
• 性质：除具有平行四边形的所有性质外，还具有四条边都相等，对角线互相垂直且平分每一组对角的性质。即\(AB = BC = CD = DA\)，\(AC\perp BD\)，\(AC\)平分\(\angle BAD\)与\(\angle BCD\)，\(BD\)平分\(\angle ABC\)与\(\angle ADC\)。
• 判定：有一组邻边相等的平行四边形是菱形；对角线互相垂直的平行四边形是菱形；四条边都相等的四边形是菱形。

1. 正方形

• 定义：有一组邻边相等且有一个角是直角的平行四边形叫做正方形。
• 性质：具有矩形和菱形的所有性质，即四条边相等，四个角都是直角，对角线互相垂直平分且相等，每一条对角线平分一组对角。
• 判定：先判定是矩形，再证明一组邻边相等；先判定是菱形，再证明有一个角是直角；有一组邻边相等且有一个角是直角的平行四边形是正方形。

三角形中位线定理

1. 定义：连接三角形两边中点的线段叫做三角形的中位线。
2. 定理：三角形的中位线平行于三角形的第三边，并且等于第三边的一半。例如，在\(\triangle ABC\)中，\(D\)、\(E\)分别是\(AB\)、\(AC\)的中点，则\(DE\parallel BC\)，\(DE = \frac{1}{2}BC\)。该定理在证明线段平行关系和计算线段长度时经常用到。

第十九章：一次函数

变量与函数

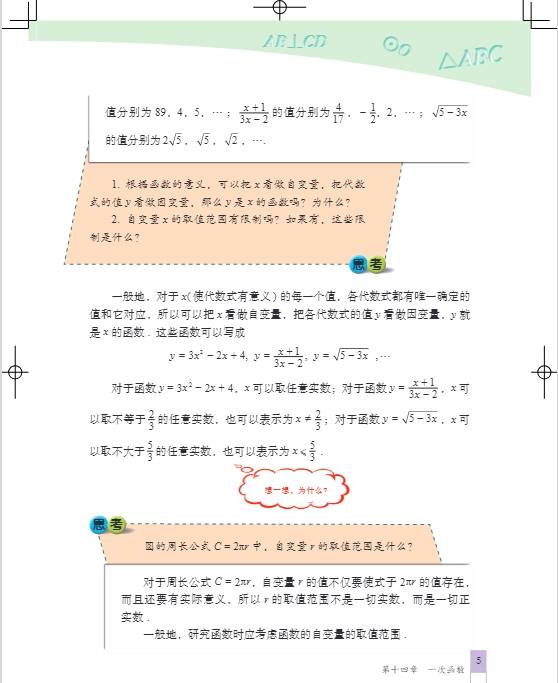
1. 变量：在一个变化过程中，数值发生变化的量称为变量。变量分为自变量和因变量，例如在路程\(s = vt\)（\(v\)为速度，\(t\)为时间）中，若速度\(v\)保持不变，时间\(t\)是自变量，路程\(s\)是因变量，\(t\)的变化会引起\(s\)的变化。
2. 函数：一般地，在一个变化过程中，如果有两个变量\(x\)与\(y\)，并且对于\(x\)的每一个确定的值，\(y\)都有唯一确定的值与其对应，那么我们就说\(x\)是自变量，\(y\)是\(x\)的函数。例如，\(y = 2x + 1\)，对于\(x\)的每一个取值，都能通过这个式子计算出唯一的\(y\)值，所以\(y\)是\(x\)的函数。

函数的图象

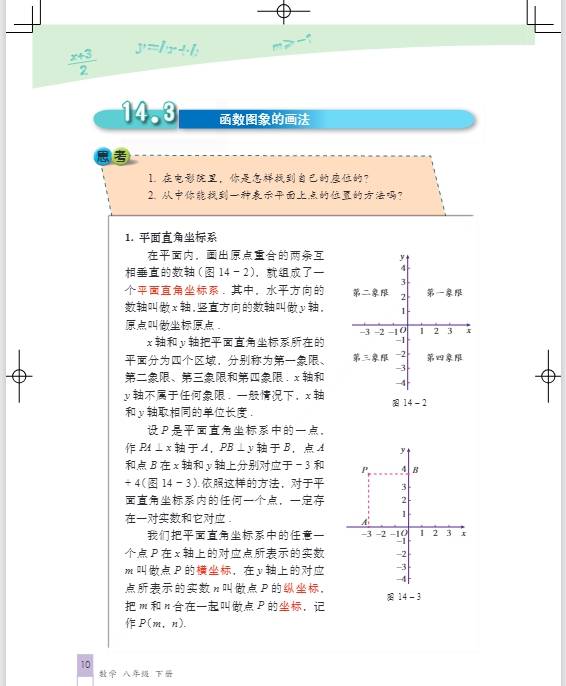
1. 平面直角坐标系：由两条互相垂直、原点重合的数轴组成。水平的数轴称为\(x\)轴或横轴，取向右为正方向；竖直的数轴称为\(y\)轴或纵轴，取向上为正方向。两坐标轴的交点为平面直角坐标系的原点。利用平面直角坐标系可以确定平面内点的位置，点的坐标用\((x,y)\)表示，其中\(x\)表示横坐标，\(y\)表示纵坐标。例如，点\(A(3, -2)\)，横坐标为\(3\)，纵坐标为\(-2\)。
2. 函数图象：一般地，对于一个函数，如果把自变量与函数的每对对应值分别作为点的横、纵坐标，那么坐标平面内由这些点组成的图形，就是这个函数的图象。例如，对于函数\(y = x\)，当\(x = 1\)时，\(y = 1\)，得到点\((1,1)\)；当\(x = -2\)时，\(y = -2\)，得到点\(( -2, -2)\)等，把这些点在平面直角坐标系中描出并连接起来，就得到函数\(y = x\)的图象，是一条经过原点且斜率为\(1\)的直线。

一次函数

1. 定义：一般地，形如\(y = kx + b\)（\(k\)，\(b\)是常数，\(k\neq0\)）的函数，叫做一次函数。当\(b = 0\)时，\(y = kx\)（\(k\neq0\)），这时\(y\)是\(x\)的正比例函数，所以正比例函数是特殊的一次函数。例如，\(y = 3x + 2\)是一次函数，\(y = -2x\)是正比例函数。
2. 性质

• 当\(k\gt0\)时，\(y\)随\(x\)的增大而增大，函数图象从左到右上升。例如在\(y = 2x + 1\)中，\(k = 2\gt0\)，\(x\)的值越大，对应的\(y\)值越大。
• 当\(k\lt0\)时，\(y\)随\(x\)的增大而减小，函数图象从左到右下降。例如在\(y = -3x + 5\)中，\(k = -3\lt0\)，\(x\)的值越大，对应的\(y\)值越小。
• \(b\)决定函数图象与\(y\)轴的交点位置，当\(b\gt0\)时，图象与\(y\)轴交于正半轴；当\(b\lt0\)时，图象与\(y\)轴交于负半轴；当\(b = 0\)时，图象经过原点。例如\(y = 2x + 3\)，图象与\(y\)轴交于点\((0,3)\)；\(y = -x - 2\)，图象与\(y\)轴交于点\((0, -2)\)。

1. 图象：一次函数\(y = kx + b\)的图象是一条直线，因此画一次函数图象时，只需确定两个点，再过这两点画直线即可，通常取与\(x\)轴、\(y\)轴的交点，即当\(y = 0\)时，\(x = -\frac{b}{k}\)，得到与\(x\)轴交点\((-\frac{b}{k},0)\)；当\(x = 0\)时，\(y = b\)，得到与\(y\)轴交点