2025年学生将迎来新版教材，新教材将更加重视思维和阅读！为了方便广大学生在暑假预习新学期的课本知识，我们整理了2025新

北师大版高中数学（上册）一电子课本，以图片的形式呈现给大家，希望对同学们的暑期学习有所帮助。

如需全套电子课本PDF版，请关注公众号“桃李科普”回复：“电子课本”

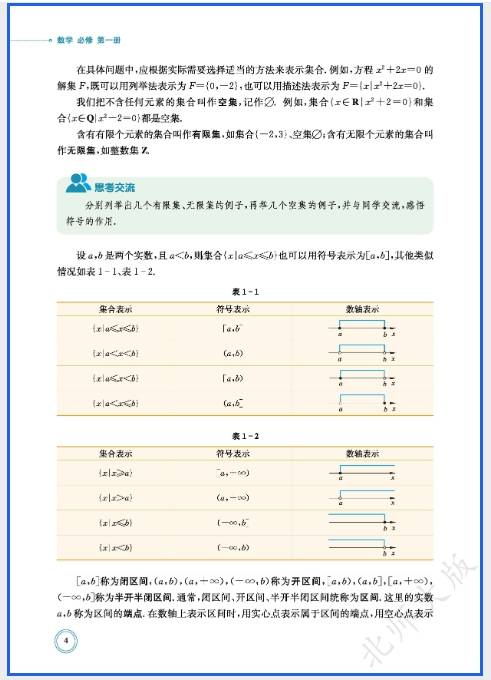
北师大版高中数学（上册）电子课本在线阅读

高中数学是衔接初中数学与高等数学的关键阶段，核心在于从 “具象计算” 转向 “抽象逻辑与综合应用”，其知识体系围绕函数、几何、代数、概率统计四大板块展开，兼具 “工具性”（如导数用于分析变化率）和 “逻辑性”（如立体几何证明）。以下从知识框架、核心难点、学习策略、备考方向四方面系统梳理，帮你搭建高中数学的 “认知地图”，高效突破重难点：

一、高中数学知识框架（必修 + 选择性必修，按模块拆解）

高中数学教材（人教 A 版）分为 “必修”（2 册）和 “选择性必修”（3 册），各模块层层递进，覆盖高考所有考点，可按 “基础工具→核心难点→综合应用” 分为三类：

模块类型包含内容核心作用高考占比基础工具模块集合、常用逻辑用语、不等式、三角函数、平面向量、统计与概率为后续学习打基础（如集合是函数的前提，向量可辅助几何计算）30%-35%核心难点模块函数（指数、对数、幂函数）、导数及其应用、立体几何、圆锥曲线高考压轴题集中区，考查逻辑推导与综合应用能力50%-55%综合拓展模块数列、计数原理、随机变量及其分布、不等式选讲（部分地区）衔接高等数学，考查知识整合与创新思维10%-15%

各模块核心知识点（高考高频考点）：

1. 函数板块（高中数学 “基石”，贯穿始终）：

• 基础：函数的定义（映射）、定义域 / 值域、单调性、奇偶性、周期性、对称性（如 “f (x+1) 是偶函数，则 f (x) 关于 x=1 对称”）；
• 具体函数：指数函数（y=aˣ）、对数函数（y=logₐx）、幂函数（y=xⁿ）的图像与性质，三角函数（sinx、cosx、tanx）的诱导公式、两角和差公式、二倍角公式；
• 应用：函数与方程（零点存在定理）、函数模型（如 “增长率问题” 用指数函数建模）。

1. 导数板块（高考压轴题核心，考查 “变化率与最优化”）：

• 基础：导数的定义（瞬时变化率）、基本求导公式（如 (xⁿ)’=nxⁿ⁻¹，(sinx)’=cosx）、导数的四则运算、复合函数求导（如 f (g (x))’=f’(g (x))・g’(x)）；
• 应用：用导数判断函数单调性（f’(x)>0→增，f’(x)<0→减）、求极值与最值（导数为 0 的点结合单调性判断）、切线方程（f’(x₀) 是切线斜率）、生活中的最优化问题（如 “求利润最大值”“求体积最大的几何体”）。

1. 几何板块（分 “立体几何” 和 “解析几何”，考查 “空间想象与代数运算”）：

• 立体几何：空间几何体的表面积与体积（圆柱、圆锥、球）、点线面的位置关系（平行、垂直），证明定理（如 “线面平行：线平行于面内一条线且线不在面内”），空间向量（用坐标法求解线面角、二面角，降低空间想象难度）；
• 解析几何：直线方程（点斜式、两点式）、圆的方程（标准式 (x-a)²+(y-b)²=r²）、圆锥曲线（椭圆、双曲线、抛物线的定义、标准方程、几何性质，如椭圆的离心率 e=c/a<1，双曲线的渐近线）。

1. 代数板块（数列、不等式，考查 “递推逻辑与运算技巧”）：

• 数列：等差数列（通项 aₙ=a₁+(n-1) d，前 n 项和 Sₙ=n (a₁+aₙ)/2）、等比数列（通项 aₙ=a₁qⁿ⁻¹，前 n 项和 Sₙ=a₁(1-qⁿ)/(1-q)），递推数列（如 “aₙ₊₁=2aₙ+1”，用构造法求通项）；
• 不等式：一元二次不等式（用图像法求解，如 x²-2x-3>0 的解集为 (-∞,-1)∪(3,+∞)）、基本不等式（a+b≥2√(ab)，a,b>0，用于求最值）。

二、高中数学核心难点与突破方法

高中数学的 “难” 集中在 “抽象概念理解”“多模块综合”“解题思路构建” 三方面，针对不同难点有明确的突破路径：

难点 1：抽象概念理解（如函数、导数、空间向量）

• 问题表现：能背公式，但不会用（如 “知道导数的定义，却不懂‘导数是切线斜率’”）；面对抽象函数（无具体表达式）无从下手（如 “已知 f (x) 是奇函数，且 f (x+2)=-f (x)，求周期”）。
• 突破方法：用 “具象化工具” 拆解抽象概念：

1. 图像辅助：函数的性质（单调性、奇偶性）用图像理解（如偶函数关于 y 轴对称，奇函数关于原点对称），导数的几何意义用 “切线” 直观感受（如 f’(x₀)>0，切线向上倾斜，函数在 x₀处递增）；
2. 实例代入：抽象函数问题，先代入具体函数验证（如 “f (x+2)=-f (x)”，可先假设 f (x)=sinx，验证周期为 4，再推广到一般情况）；
3. 定义推导：不要死记公式，亲手推导核心定义（如推导 “导数的四则运算公式”“三角函数的二倍角公式”），理解公式的 “来龙去脉”。

难点 2：多模块综合题（如 “导数 + 函数 + 不等式”“立体几何 + 空间向量 + 三角函数”）

• 问题表现：单独做某一模块的题会，但遇到综合题（如 “用导数证明不等式 f (x)>g (x)”）就卡壳，不知道 “该调用哪个知识点”。
• 突破方法：“拆题→联知识点→建逻辑链” 三步法：例：“证明当 x>0 时，x - ln (x+1) > 0”（导数 + 函数 + 不等式综合）：

1. 拆题：目标是 “证明 x>0 时，h (x)=x - ln (x+1) > 0”，需先分析 h (x) 的单调性；
2. 联知识点：“分析单调性” 需用导数，即求 h’(x)；
3. 建逻辑链：

• 第一步：求 h (x) 的定义域（x>-1，结合条件 x>0，定义域为 x>0）；
• 第二步：求导 h’(x)=1 - 1/(x+1) = x/(x+1)；
• 第三步：判断 h’(x) 在 x>0 时的符号（x>0→h’(x)>0→h (x) 在 (0,+∞) 单调递增）；
• 第四步：求 h (x) 的最小值（h (0)=0 - ln1=0，单调递增→x>0 时 h (x)>h (0)=0），得证。关键：每一步都明确 “用什么知识点”，避免 “凭感觉做题”。

难点 3：解题思路构建（如立体几何证明、圆锥曲线计算）

• 问题表现：面对 “证明线面垂直”“求椭圆与直线的交点弦长”，不知道 “从哪开始想”，只能盲目尝试。