内容聚焦初中几何基础模块中的相交线相关知识，属于平面几何入门阶段的核心内容。几何作为数学学科的重要分支，主要研究图形的位置关系与数量关系，而相交线是平面内两条直线最基本的位置关系之一，是学生从数的运算过渡到形的研究的关键衔接点。对于刚接触几何的学生而言，这部分知识是构建几何思维的起点，其学习效果直接影响后续更复杂几何内容的理解。图片通过清晰的分类与实例，将抽象的几何概念转化为具体可感知的知识要点，帮助学生建立对几何定义、性质、推理的初步认知。这部分内容既承接了小学阶段对直线、角的基础认知，又为后续平行线、三角形、四边形等几何知识的学习搭建了桥梁，是几何知识体系中不可或缺的基础环节，对学生形成完整的数学知识框架具有重要意义。

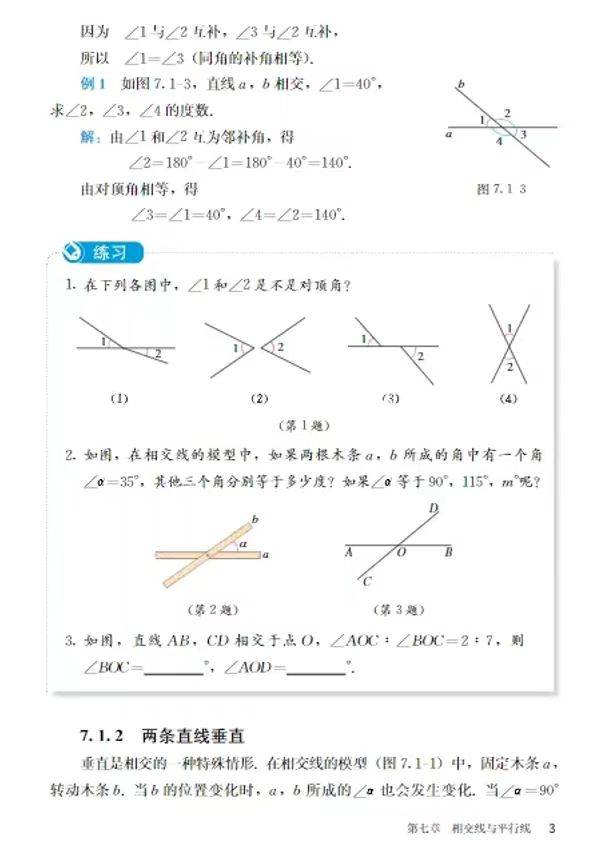
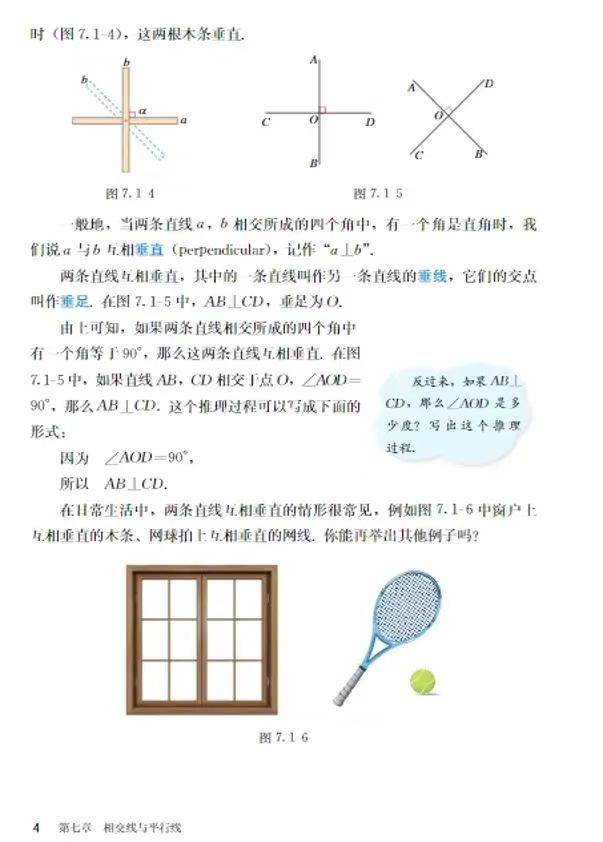
内容主要涵盖两方面核心知识：两条直线相交的基本概念与性质，包括邻补角的定义、两角之和为 180° 的数量关系，对顶角的定义及相等的性质，同时通过具体例题展示知识点的应用；两条直线垂直的相关内容，明确垂直是相交的特殊情形，给出垂直的定义、表示方法，推导得出垂直的双向推理逻辑，并用生活实例辅助理解。

对学生学习的帮助体现在多个层面：帮助学生精准掌握几何基本概念，建立 “定义 — 性质 — 应用” 的认知模式，培养严谨的逻辑思维；通过实例分析，让学生学会将抽象几何知识与具体情境结合，提升知识应用能力；为后续几何学习奠定基础，使学生逐步适应几何推理的思维方式，理解几何知识的连贯性与系统性，为更复杂的几何证明、图形分析提供方法支撑。

相交线相关知识的学习，是学生几何学习旅程中的重要起步。这部分内容看似基础，却承载着培养学生空间想象能力、逻辑推理能力的重要使命。通过对邻补角、对顶角、垂直等知识点的学习，学生不仅能掌握具体的几何知识，更能初步形成几何学科的思维习惯，学会用严谨的语言表达几何关系，用逻辑推理验证几何结论。这些能力与习惯的培养，不仅适用于数学学科的学习，更能迁移到其他需要逻辑分析的学科中，对学生综合素养的形成具有长远意义。同时，这部分知识在生活中有着广泛应用，帮助学生发现生活中的几何规律，体会数学与生活的联系，激发学习数学的内在动力。作为几何知识体系的基础，相交线相关内容为学生后续深入学习几何知识打开了大门，为进一步探索更复杂的图形关系、解决更具挑战性的数学问题提供了坚实的基础保障。