冀教版八年级数学（下册）电子课本可以方便大家随时随地预习或复习课本知识，为此，我们找到了冀教版八年级数学（下册）新教材电子书教材的全部内容，以高清图片的形式呈现给大家，希望能够提高大家的学习效率。

如需全套电子课本PDF版，请关注公众号“桃李文库”回复：“电子课本”

冀教版八年级数学（下册）新教材电子课本在线阅读（此为截图版，获取是高清版

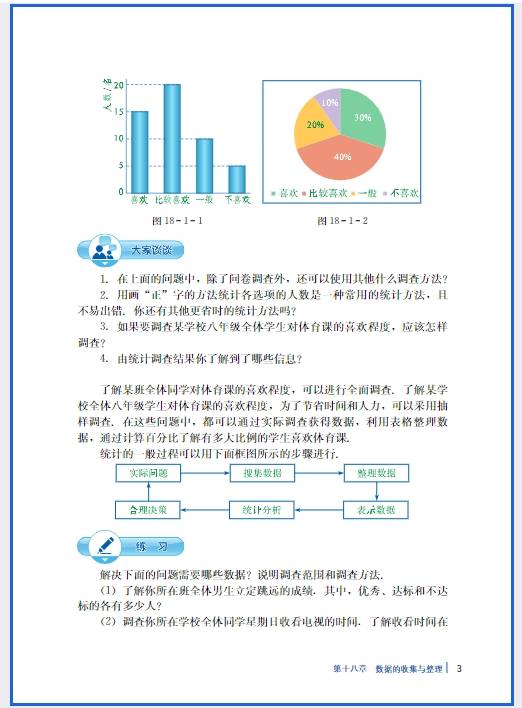
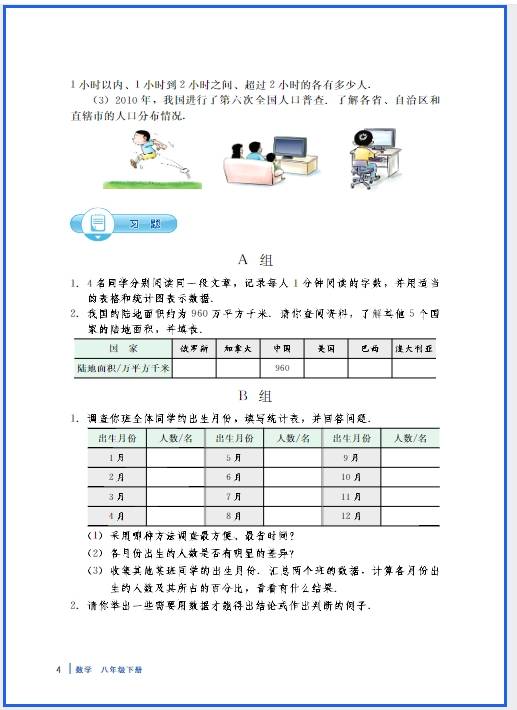
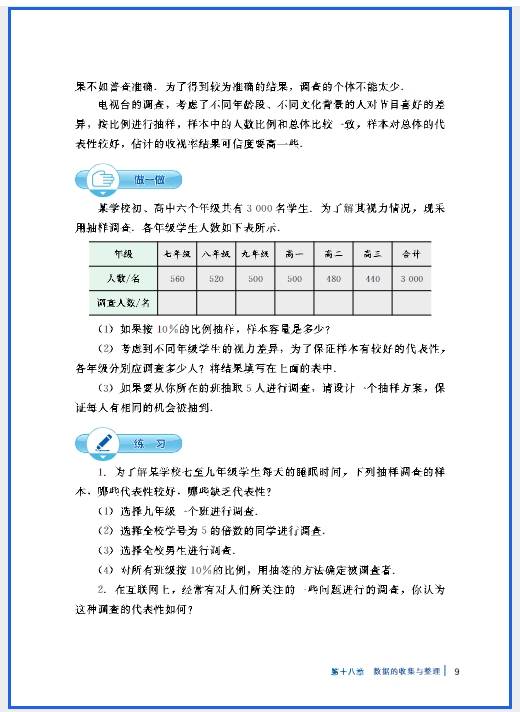
八年级阶段的数学思维训练，需结合该学段核心知识（函数、几何、方程），聚焦逻辑推理、模型构建、转化迁移三大核心能力，通过针对性训练提升解题思路和综合应用能力，以下是分维度的训练方法和具体实操方案：

一、代数思维：从 “计算” 到 “建模”，强化抽象逻辑

代数思维的核心是用符号和关系式表示数量关系，八年级重点训练 “方程 / 函数建模” 和 “代数变形” 能力。

1. 变量关系感知训练

• 实操方法：从生活场景提炼数量关系，比如 “手机话费套餐（月租 + 每分钟资费）” 对应一次函数\(y=kx+b\)；“路程固定时速度与时间的关系” 对应反比例函数\(y=\frac{k}{x}\)，每天 1 个场景，用代数式或函数式表达。
• 进阶训练：给一个函数解析式，反向编生活应用题，比如\(y=0.5x+20\)，可编 “文具店买笔记本，每本 0.5 元，另收 20 元运费，总费用 y 与购买数量 x 的关系”，强化 “式→实际” 的逆向建模。

1. 代数变形与推理训练

• 分式 / 整式变形：做 “条件求值” 题，比如已知\(\frac{1}{x}-\frac{1}{y}=3\)，求\(\frac{2x-3xy-2y}{x-2xy-y}\)的值，通过整体代换（将\(\frac{1}{x}-\frac{1}{y}=3\)转化为\(y-x=3xy\)）解题，总结 “化繁为简、整体代入” 的变形技巧。
• 方程逻辑推理：针对分式方程 “增根”“无解” 问题，分析 “整式方程解为增根→分母为 0” 的逻辑链，比如分式方程\(\frac{x-1}{x-2}=\frac{m}{x-2}\)有增根，推导增根为\(x=2\)，代入整式方程\(x-1=m\)得\(m=1\)，强化 “条件→结论” 的严谨推理。

二、几何思维：从 “识图” 到 “构图”，提升空间推理

几何思维的核心是图形性质的应用和辅助线构造，八年级重点训练 “定理联想” 和 “转化转化” 能力。

1. 定理联动训练

• 实操方法：整理几何定理 “条件清单”，比如看到 “平行四边形”，立刻联想 “对边平行且相等、对角线互相平分”；看到 “直角三角形”，联想 “勾股定理、斜边上的中线等于斜边一半”。
• 专项练习：做 “多定理综合题”，比如 “矩形 ABCD 中，对角线 AC、BD 交于 O，AE⊥BD 于 E，求证 OE・OB=AE²”，需联动 “矩形对角线相等且平分”“直角三角形射影定理”，训练定理的串联应用。

1. 辅助线构造训练

• 分类总结：按题型整理常用辅助线，形成 “条件→辅助线” 的条件反射：
• 勾股定理：遇线段长度求算，作垂线构造直角三角形（比如求不规则三角形边长，作高转化为两个直角三角形）；
• 平行四边形：遇 “中点”，连接对角线或构造中位线；遇 “线段相等”，作平行线转化为全等三角形；
• 特殊四边形：正方形 / 菱形中，连对角线利用垂直 / 平分性质。
• 实操练习：每天 1 道几何题，先不看答案，尝试 3 种以上辅助线画法，再对比最优解法，强化 “构图” 思路。

三、函数思维：从 “图像” 到 “数形结合”，打通数与形的关联

函数是八年级数学的核心，思维训练重点是数形互译，即 “图像特征→代数性质” 和 “代数关系→图像形态” 的转化。

1. 图像信息提取训练

• 实操方法：给一次函数 / 反比例函数图像，标注关键点（与坐标轴交点、与其他函数交点、顶点），从图像直接读取 “增减性、k 的符号、自变量取值范围”，比如 “一次函数图像从左到右下降→k＜0”“反比例函数在二、四象限→k＜0”。
• 对比训练：画\(y=2x+1\)和\(y=-2x+1\)的图像，对比 k 的符号对倾斜方向的影响；画\(y=\frac{4}{x}\)和\(y=-\frac{4}{x}\)的图像，对比 k 的符号对象限的影响，总结 “数→形” 的对应规律。

1. 数形结合综合训练

• 核心题型：一次函数与几何图形的综合题，比如 “在平面直角坐标系中，一次函数\(y=x+1\)与 x 轴、y 轴交于 A、B 两点，以 AB 为边作正方形，求正方形顶点坐标”，需结合 “函数交点坐标计算”“正方形边长 / 角度性质”“坐标系内点的坐标规律”，训练多知识融合的解题思维。

四、综合思维：从 “单点解题” 到 “系统迁移”，提升综合应用

1. 错题溯源与变式训练

• 整理错题时，不仅标注错误原因，还要改编题目：比如把 “一次函数应用题” 的 “行程背景” 改成 “利润背景”，把 “平行四边形证明题” 的 “已知对边平行” 改成 “已知对角线平分”，通过变式训练，掌握 “换场景不换方法” 的迁移能力。

1. 一题多解与最优解选择

• 针对中档以上题型，尝试多种解法，比如 “求直角三角形斜边上的高”，可用面积法（\(\frac{1}{2}ab=\frac{1}{2}ch\)）、相似三角形、勾股定理 + 方程，对比不同方法的效率，总结 “题型→最优解法” 的匹配规律，提升解题速度和灵活性。

五、每日实操训练计划（适配八年级，碎片化时间可完成）

1. 基础训练（15 分钟 / 天）：1 道代数变形题 + 1 道几何定理应用填空题，巩固基础逻辑；
2. 专项训练（30 分钟 / 天）：隔天轮换 “函数建模”“几何辅助线”“综合数形题”，深度攻克一个模块；
3. 周末复盘（60 分钟 / 周）：整理一周的训练错题，归纳同类题型的解题模板，比如 “分式方程应用题步骤”“平行四边形判定的 3 种常用路径”。