苏教版六年级数学（上下册）电子课本可以方便大家随时随地预习或复习课本知识，为此，我们找到了苏教版六年级数学（上下册）新教材电子书教材的全部内容，以高清图片的形式呈现给大家，希望能够提高大家的学习效率。

如需全套电子课本PDF版，请关注公众号“桃李百科”回复：“电子课本”

苏教版六年级数学（上下册）新教材电子课本在线阅读（此为截图版，获取是高清版）

六年级上册

1. 第一单元：长方体和正方体

• 知识要点：认识长方体和正方体的特征，长方体有 6 个面，相对的面完全相同；12 条棱，相对的棱长度相等；8 个顶点。正方体是特殊的长方体，它的 6 个面都是完全相同的正方形，12 条棱长度都相等。掌握长方体和正方体的表面积计算公式，长方体表面积\(S=(ab + ah + bh)×2\)（其中\(a\)为长，\(b\)为宽，\(h\)为高），正方体表面积\(S = 6a²\)（\(a\)为棱长）。体积计算公式为长方体体积\(V = abh\)，正方体体积\(V = a³\)。还有容积的概念，容积的计算方法与体积类似，但要从容器里面测量长、宽、高。
• 应用拓展：在实际生活中，可用于计算物体的用料面积，如制作一个长方体形状的无盖鱼缸需要多少玻璃，就可利用长方体表面积公式计算 5 个面的面积之和；计算物体所占空间大小，像一个正方体箱子能装多少东西，运用正方体体积公式求解；以及计算容器的容积，如长方体水箱能装多少升水等问题。

1. 第二单元：分数乘法

• 知识要点：理解分数乘法的意义，分数乘整数表示求几个相同分数的和的简便运算，如\(\frac{3}{5}×4\)表示 4 个\(\frac{3}{5}\)相加；分数乘分数表示求一个分数的几分之几是多少，如\(\frac{3}{5}×\frac{2}{3}\)表示求\(\frac{3}{5}\)的\(\frac{2}{3}\)是多少。掌握分数乘法的计算方法，分子相乘的积作分子，分母相乘的积作分母，能约分的先约分。例如\(\frac{4}{7}×\frac{3}{8}=\frac{4×3}{7×8}=\frac{3}{14}\)。同时要知道一个数乘分数，积与这个数的大小关系，当乘大于 1 的分数时，积大于这个数；乘小于 1 的分数时，积小于这个数；乘 1 时，积等于这个数。
• 应用拓展：可解决如求一个数的几分之几是多少的实际问题。例如，果园里有苹果树 200 棵，梨树的棵数是苹果树的\(\frac{3}{4}\)，那么梨树有\(200×\frac{3}{4}=150\)棵。还能解决连续求一个数的几分之几是多少的问题，如一本书有 120 页，第一天看了全书的\(\frac{1}{3}\)，第二天看了第一天的\(\frac{3}{4}\)，第二天看的页数为\(120×\frac{1}{3}×\frac{3}{4}=30\)页。

1. 第三单元：分数除法

• 知识要点：理解分数除法的意义，与整数除法意义相同，已知两个因数的积与其中一个因数，求另一个因数的运算。如已知\(\frac{2}{3}×x=\frac{4}{9}\)，求\(x\)，用除法\(x=\frac{4}{9}÷\frac{2}{3}\)。掌握分数除法的计算方法，除以一个数（0 除外）等于乘这个数的倒数，如\(\frac{4}{9}÷\frac{2}{3}=\frac{4}{9}×\frac{3}{2}=\frac{2}{3}\)。理解比的意义，两个数相除又叫做两个数的比，如\(5÷3\)可写成\(5:3\)，比的前项除以后项所得的商叫做比值，\(5:3\)的比值是\(\frac{5}{3}\)。掌握比的基本性质，比的前项和后项同时乘或除以相同的数（0 除外），比值不变，利用此性质可进行比的化简，如\(12:18=(12÷6):(18÷6)=2:3\)。
• 应用拓展：能解决已知一个数的几分之几是多少，求这个数的实际问题。例如，小明有 15 本书，是小红书数量的\(\frac{3}{5}\)，则小红有书\(15÷\frac{3}{5}=15×\frac{5}{3}=25\)本。还能运用比解决按比例分配问题，如一个三角形三个内角的度数比是\(2:3:4\)，内角和是 180°，那么三个角分别为\(180°×\frac{2}{2 + 3 + 4}=40°\)，\(180°×\frac{3}{2 + 3 + 4}=60°\)，\(180°×\frac{4}{2 + 3 + 4}=80°\)。

1. 第四单元：解决问题的策略

• 知识要点：学会运用假设和替换的策略解决实际问题。例如在解决 “鸡兔同笼” 类型问题时，可假设全是鸡或全是兔，通过计算脚数的差异来求解鸡和兔的数量；在一些物品组合问题中，可根据条件进行等量替换，把两种或多种物品转化为一种物品来计算。
• 应用拓展：解决类似 “买 3 支铅笔和 2 支钢笔共花 12 元，1 支钢笔的价钱等于 3 支铅笔的价钱，铅笔和钢笔的单价各是多少” 这样的问题，可将 2 支钢笔替换为\(2×3 = 6\)支铅笔，那么相当于买\(3 + 6 = 9\)支铅笔花了 12 元，从而求出铅笔单价为\(12÷9=\frac{4}{3}\)元，进而得出钢笔单价为\(\frac{4}{3}×3 = 4\)元。通过这些策略培养学生分析问题、解决问题的能力，提高思维的灵活性。

1. 第五单元：分数四则混合运算

• 知识要点：掌握分数四则混合运算的运算顺序，与整数四则混合运算顺序相同，先算乘除，后算加减，有括号的先算括号里面的。例如计算\(\frac{1}{2} + \frac{3}{4}×\frac{2}{3}÷2\)，先算乘法\(\frac{3}{4}×\frac{2}{3}=\frac{1}{2}\)，再算除法\(\frac{1}{2}÷2=\frac{1}{4}\)，最后算加法\(\frac{1}{2}+\frac{1}{4}=\frac{3}{4}\)。整数的运算律在分数运算中同样适用，如加法交换律\(a + b = b + a\)，乘法分配律\(a×(b + c)=a×b + a×c\)等，运用运算律可使计算简便。如计算\(\frac{3}{7}×\frac{5}{9}+\frac{4}{7}×\frac{5}{9}\)，可利用乘法分配律\((\frac{3}{7}+\frac{4}{7})×\frac{5}{9}=1×\frac{5}{9}=\frac{5}{9}\)。
• 应用拓展：用于解决更复杂的实际问题，如工程问题。一项工程，甲队单独做 10 天完成，乙队单独做 15 天完成，两队合作几天完成？把这项工程看作单位 “1”，甲队每天完成\(\frac{1}{10}\)，乙队每天完成\(\frac{1}{15}\)，两队合作每天完成\(\frac{1}{10}+\frac{1}{15}=\frac{1}{6}\)，所以合作完成需要\(1÷\frac{1}{6}=6\)天。通过分数四则混合运算解决各种实际问题，提高学生综合运用数学知识的能力。

1. 第六单元：百分数

• 知识要点：理解百分数的意义，百分数表示一个数是另一个数的百分之几，也叫百分率或百分比，如\(35\%\)表示一个数占另一个数的\(\frac{35}{100}\)。掌握百分数与小数、分数的互化方法，百分数化小数，去掉百分号，小数点向左移动两位，如\(60\% = 0.6\)；小数化百分数，小数点向右移动两位，加上百分号，如\(0.25 = 25\%\)。百分数化分数，先写成分母是 100 的分数，再化简，如\(45\%=\frac{45}{100}=\frac{9}{20}\)；分数化百分数，先把分数化成小数（除不尽时，通常保留三位小数），再化成百分数，如\(\frac{3}{8}=0.375 = 37.5\%\)。会求常见的百分率，如出勤率\(=\frac{出勤人数}{总人数}×100\%\)，发芽率\(=\frac{发芽种子数}{种子总数}×100\%\)等。
• 应用拓展：能解决与百分数相关的实际问题，如求一个数比另一个数多（或少）百分之几，如小明有 80 分，小红有 100 分，小红比小明多\((100 - 80)÷80×100\% = 25\%\)；已知一个数，求比这个数多（或少）百分之几的数是多少，如一件商品原价 200 元，现在降价\(10\%\)，则现在价格为\(200×(1 - 10\%) = 200×0.9 = 180\)元；以及已知比一个数多（或少）百分之几的数是多少，求这个数，如小明有 120 本书，比小红多\(20\%\)，则小红有书\(120÷(1 + 20\%) = 120÷1.2 = 100\)本。在生活中，百分数广泛应用于折扣、利率、增长率等问题的计算。

六年级下册

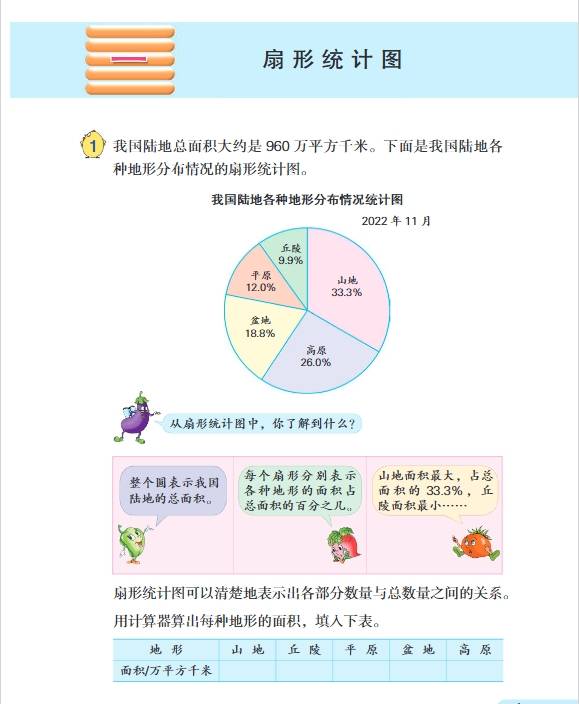
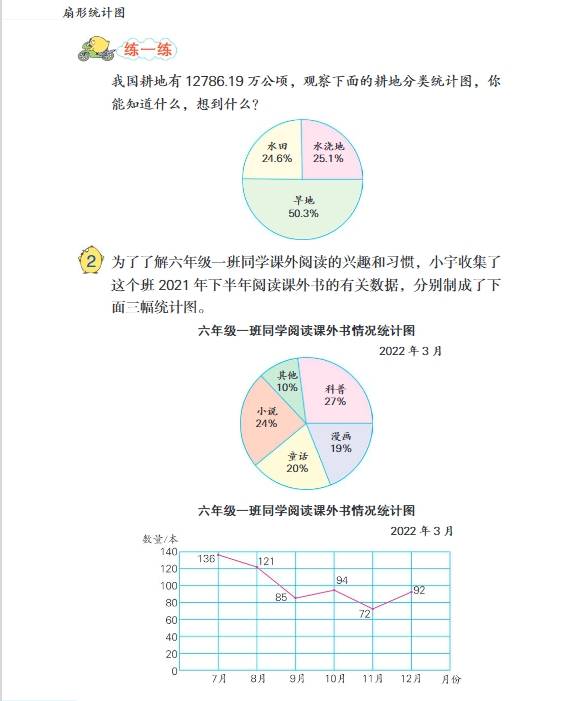
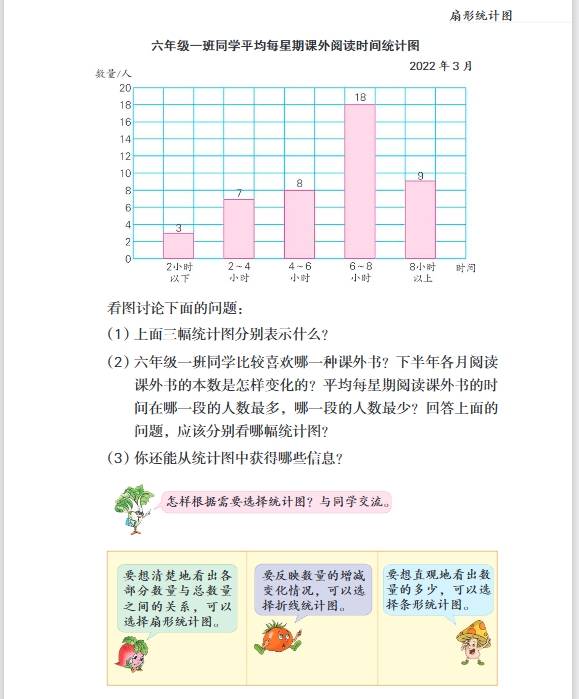
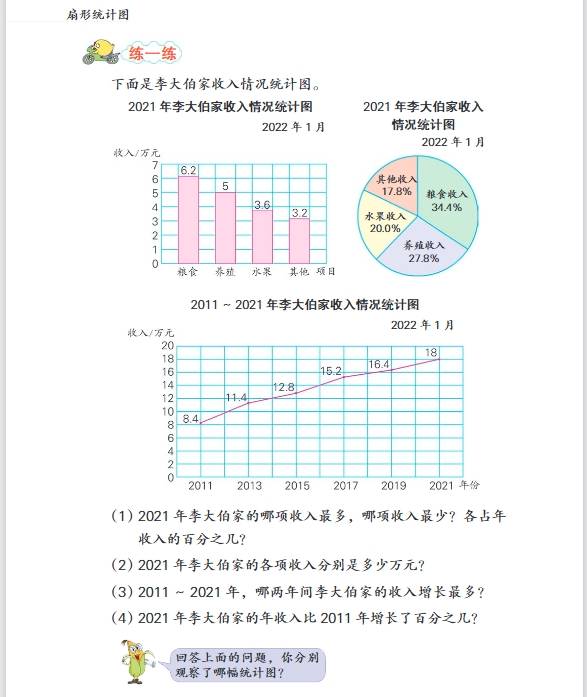
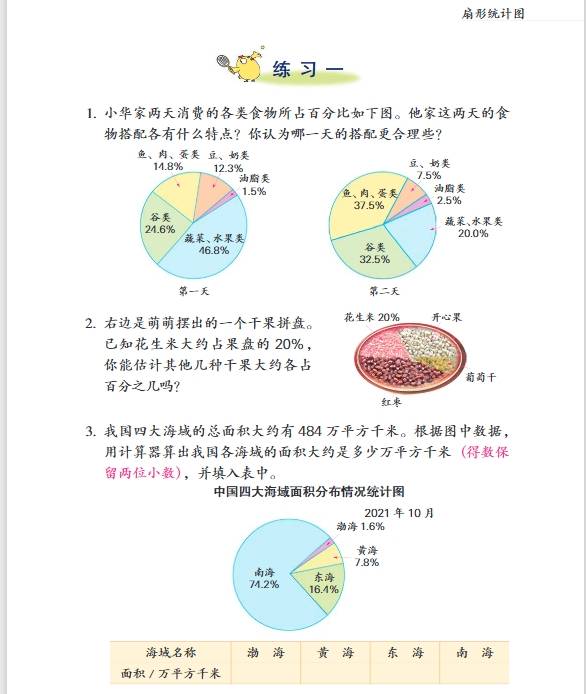
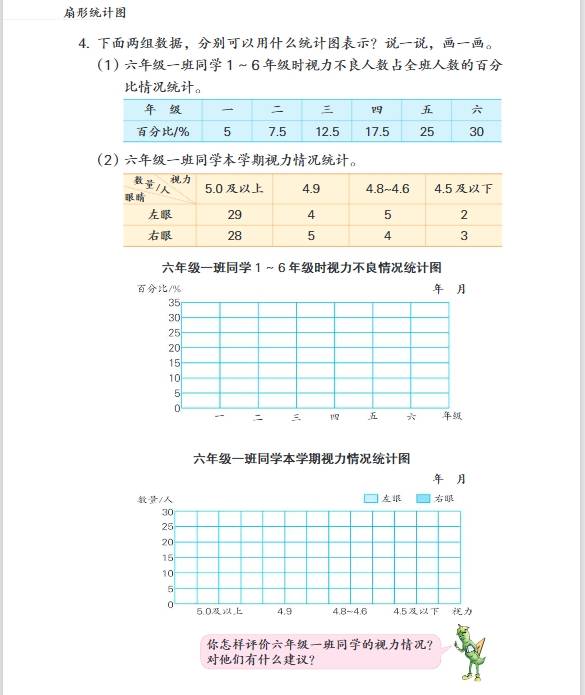
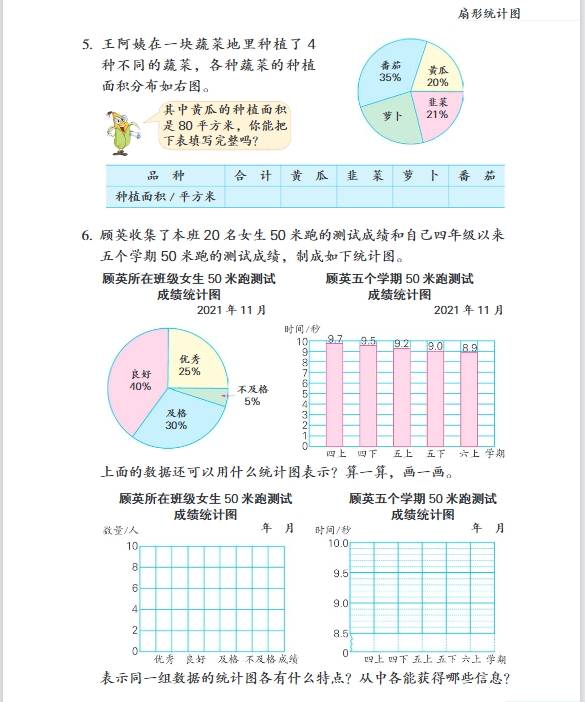
1. 第一单元：扇形统计图

• 知识要点：认识扇形统计图的特点，它可以清楚地反映出各部分数量与总数量之间的关系。通过扇形统计图能直观地看出各部分数量占总量的百分比。例如，从一个学校各年级人数占全校总人数的扇形统计图中，可以直接看出每个年级人数占全校人数的比例情况。学会根据扇形统计图提供的信息进行简单的分析和计算，如已知总数量和各部分所占百分比，求各部分数量，用总数量乘以各部分百分比即可；已知各部分数量和总数量，求各部分数量占总数量的百分比，用各部分数量除以总数量再乘以\(100\%\)。
• 应用拓展：在生活中，扇形统计图可用于分析各种统计数据，如分析家庭各项支出占总支出的比例，从而合理规划家庭财务；分析一个班级学生不同学科成绩的分布情况，帮助教师了解学生的学习状况，调整教学策略等。

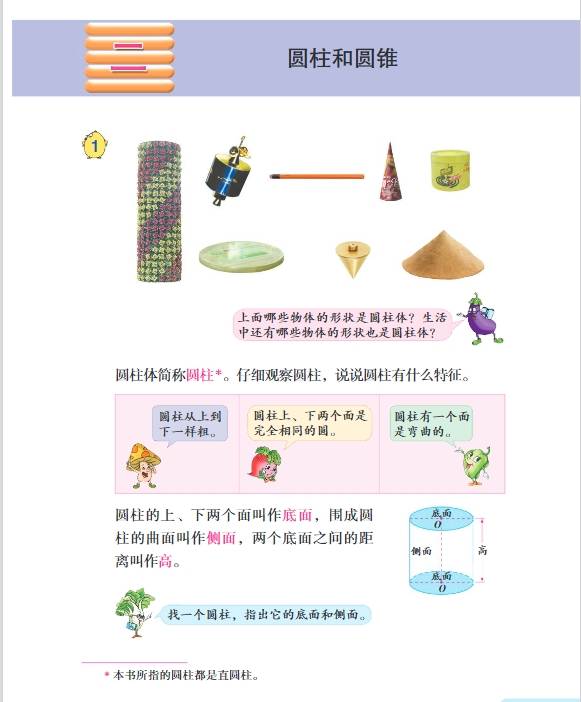
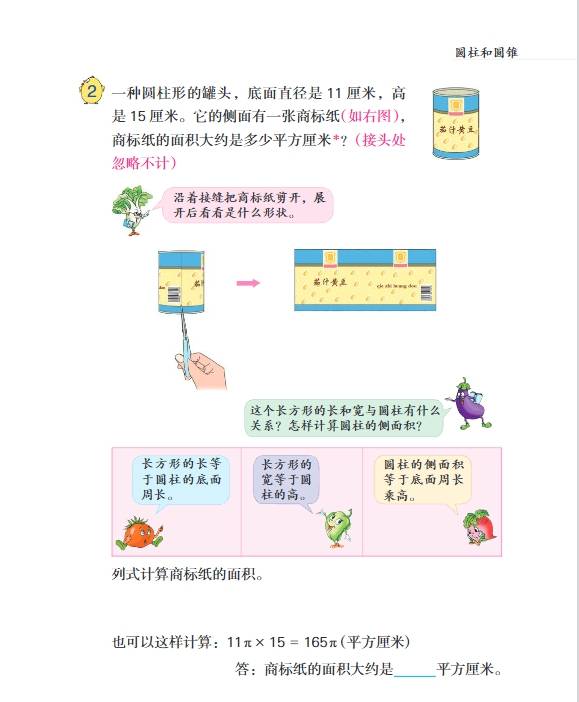
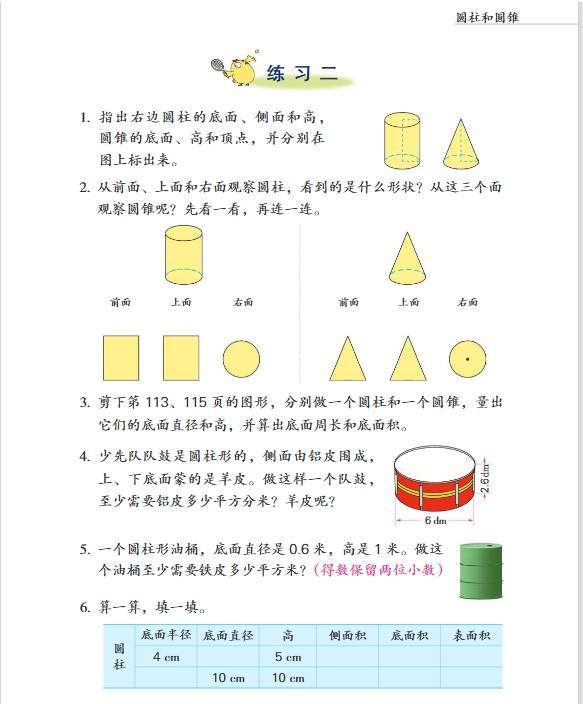
1. 第二单元：圆柱和圆锥

• 知识要点：认识圆柱和圆锥的特征，圆柱有两个底面，是完全相同的圆，侧面是一个曲面，展开后是一个长方形（当底面周长和高相等时是正方形），圆柱的高有无数条；圆锥有一个底面，是一个圆，侧面是一个曲面，展开后是一个扇形，圆锥只有一条高。掌握圆柱的表面积公式\(S = 2πr² + 2πrh\)（\(S\)为表面积，\(r\)为底面半径，\(h\)为高），体积公式\(V = πr²h\)；圆锥的体积公式\(V=\frac{1}{3}πr²h\)。如一个圆柱底面半径是 3 厘米，高是 5 厘米，表面积为\(2×3.14×3² + 2×3.14×3×5 = 150.72\)平方厘米，体积为\(3.14×3²×5 = 141.3\)立方厘米；一个圆锥底面半径是 2 厘米，高是 6 厘米，体积为\(\frac{1}{3}×3.14×2²×6 = 25.12\)立方厘米。
• 应用拓展：能运用圆柱和圆锥的知识解决实际问题，如求圆柱形水桶的容积、圆锥形沙堆的体积等。如用铁皮制作一个无盖的圆柱形水桶，底面直径 6 分米，高 8 分米，需要铁皮的面积为\(3.14×(6÷2)² + 3.14×6×8 = 178.98\)平方分米，水桶容积为\(3.14×(6÷2)²×8 = 226.08\)立方分米。在建筑、制造等领域，圆柱和圆锥的知识有广泛应用，如圆柱形柱子的设计、圆锥形屋顶的建造等。

1. 第三单元：解决问题的策略

• 知识要点：进一步学习用转化的策略解决问题，将复杂的问题转化为简单的、熟悉的问题来解决。例如在计算不规则图形的面积时，可通过割补、平移等方法将其转化为规则图形来计算；在解决一些分数、百分数问题时，可通过转化单位 “1”，使问题更容易求解。
• 应用拓展：如在计算一个由多个不规则图形组成的花坛面积时，可把各个不规则图形通过平移、旋转等方式转化为长方形、三角形等规则图形，再分别计算面积后相加。在解决 “某工厂去年生产产品的数量比前年增加\(20\%\)，今年生产产品的数量比去年减少\(20\%\)，今年生产产品的数量与前年相比是增加还是减少” 这样的问题时，可把前年生产产品数量看作单位 “1”，通过转化计算出今年生产产品数量是前年的\((1 + 20\%)×(1 - 20\%) = 96\%\)，从而得出今年比前年减少了。通过转化策略，培养学生灵活运用知识解决问题的能力，提高思维的创造性。

1. 第四单元：比例

• 知识要点：理解比例的意义，表示两个比相等的式子叫做比例，如\(2:3 = 4:6\)。掌握比例的基本性质，在比例里，两个外项的积等于两个内项的积，如在\(2:3 = 4:6\)中，\(2×6 = 3×4\)。会解比例，根据比例的基本性质，已知比例中的任何三项，就可以求出这个比例中的另外一个未知项。如\(5:x = 10:12\)，则\(10x = 5×12\)，\(x = 6\)。认识正比例和反比例关系，两种相关联的量，一种量变化，另一种量也随着变化，如果这两种量中相对应的两个数的比值一定，这两种量就叫做成正比例的量，它们的关系叫做正比例关系，如路程 ÷ 时间 = 速度（一定），路程与时间成正比例；如果这两种量中相对应的两个数的乘积一定，这两种量就叫做成反比例的量，它们的关系叫做反比例关系，如长 × 宽 = 面积（一定），长与宽成反比例。
• 应用拓展：能运用比例知识解决实际问题，如比例尺问题，图上距离：实际距离 = 比例尺，已知比例尺和图上距离可求实际距离，已知比例尺和实际距离可求图上距离。例如，在一幅比例尺是 1:4000000 的地图上，量得甲、乙两地的距离是 5 厘米，那么甲、乙两地的实际距离是\(5×4000000 = 20000000\)厘米 = 200 千米。还可用于解决按比例分配、图形的放大与缩小等实际问题，如将一个图形按\(2:1\)放大，就是把图形的每条边都放大到原来的 2 倍。

1. 第五单元：确定位置

• 知识要点：能根据方向和距离确定物体的位置，要明确方向角的含义，如北偏东\(45°\)就是以正北方向为起始边，向东旋转\(45°\)所指的方向。知道描述路线图的方法，要清楚每一段路的方向和距离。例如描述从学校到家的路线，要依次说明每一段路是朝什么方向走，走多远。
• 应用拓展：在实际生活中，可用于绘制地图、描述行走路线、确定物体的位置等。如根据给定的信息，绘制从公园到图书馆的路线图，依次说明每一段路的方向和距离变化；在航海、航空等领域，准确确定位置至关重要，通过方向和距离能确定船只或飞机的位置，保障航行安全。

1. 第六单元：正比例和反比例

• 知识要点：深入理解正比例和反比例的意义，能根据给出的数量关系判断两种量成正比例还是反比例。除了常见的路程、速度、时间，总价、单价、数量等关系外，还能分析一些