2025年学生将迎来新版教材，新教材将更加重视思维和阅读！为了方便广大学生在暑假预习新学期的课本知识，我们整理了2025新北师大版六年级数学（上册）一电子课本，以图片的形式呈现给大家，希望对同学们的暑期学习有所帮助。

以下是部分内容截图，完整信息请查看 PDF 文件

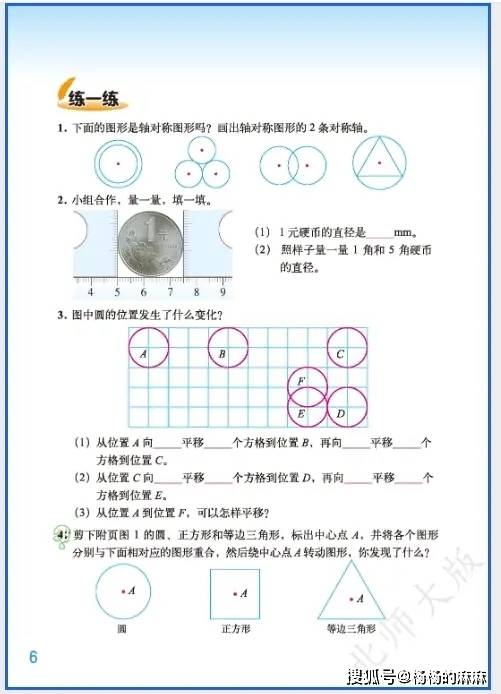
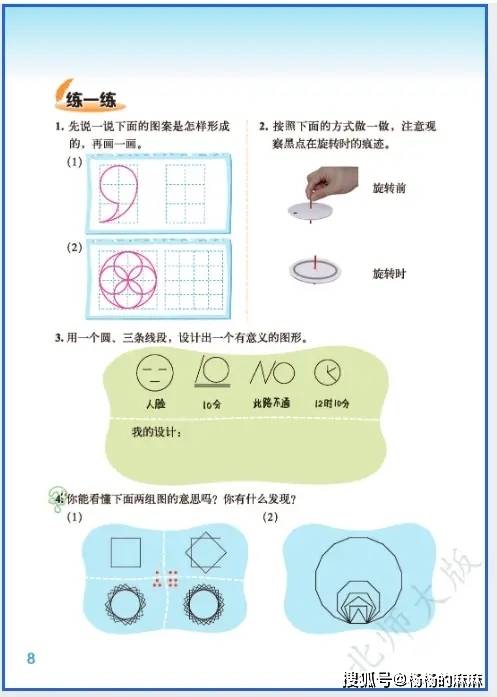
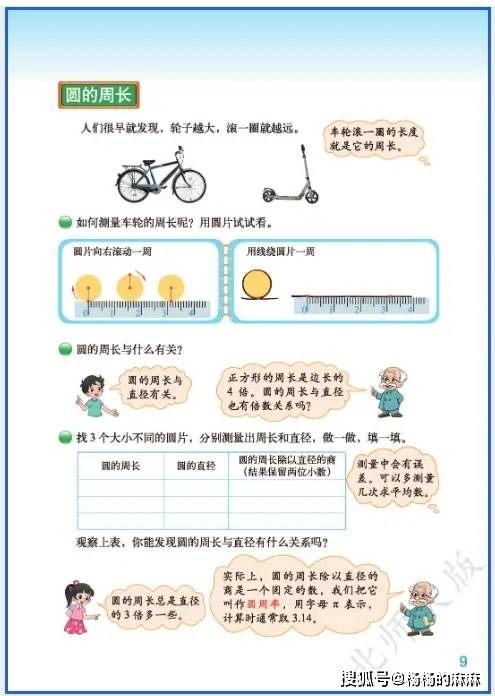
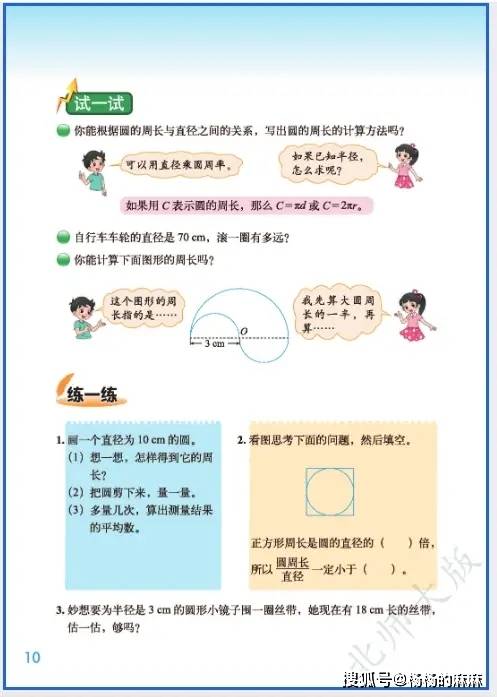
六年级数学作为小学阶段知识的整合与提升关键期，既承接了中低年级的基础内容，又为初中数学学习做好铺垫。不过，随着知识点难度加大、综合程度提高，学生在学习和解题过程中常常会遇到各类问题。下面就对六年级数学的核心易错点进行分类整理，并搭配典型错误案例与实用规避方法，助力学生避开学习误区。

一、分数、百分数应用题（高频易错，占比大）

分数与百分数是六年级数学的核心知识点，而相关应用题因涉及 “量率对应”“单位 1” 等较为抽象的概念，成为学生出错频率最高的板块。

1. “单位 1” 判断失误（基础性错误）

学生常面临的问题是无法精准锁定题目中的 “单位 1”，进而导致在计算时混淆乘除法的运用规则 —— 已知单位 1 求其几分之几用乘法，未知单位 1 求整体则用除法。通常来说，题目中 “占”“是”“比”“相当于” 这类词语后面所描述的量，以及 “的” 字前面的量，往往就是单位 1。

• 错误案例：有这样一道题 “一堆煤，用去了 2/5，还剩余 12 吨，这堆煤原本有多少吨？”，部分学生给出的解答是
• 12×(1−2/5)=7.2
• 吨。出现这种错误的原因是学生误将 “剩下的 12 吨” 当作了单位 1，错误地使用了乘法计算。
• 正确解答：这道题的单位 1 实际是 “原有煤的总吨数”，且该量未知。剩余的 12 吨对应的分率是
• 1−2/5=3/5
• ，所以原有煤的吨数应为
• 12÷3/5=20
• 吨。

2. “求一个数比另一个数多（少）几分之几 / 百分之几” 中 “量” 与 “率” 混淆

在解决这类问题时，正确的计算方法是用两个数的差值除以 “比” 字后面的量（即单位 1），但学生常常会错误地除以 “比” 字前面的量，或者把 “多（少）的具体数量” 和 “多（少）的分率 / 百分率” 混为一谈。

• 错误案例：已知 “甲数是 20，乙数是 16，甲数比乙数多百分之几？”，有些学生的解法是
• (20−16)÷20=20%
• ，这里错误地将甲数当成了单位 1；还有学生直接回答 “多 4”，混淆了 “多的具体数量” 和 “多的百分率” 这两个概念。
• 正确解答：此问题中的单位 1 是乙数，所以应该用两数的差值除以乙数，即
• (20−16)÷16=25%
• 。

3. 百分数应用题中 “率” 的叠加错误（如折扣、税率、利率问题）

当题目中出现多个 “率” 需要连续应用时，学生容易忽略单位 1 的变化，尤其是在折扣问题中；同时，对于 “应纳税额”“本金”“利息” 的计算逻辑也常常混淆。

• 错误案例：一道关于折扣的题目 “一件衣服原价 200 元，先打八折销售，之后在此基础上再打九折，这件衣服的现价是多少元？”，部分学生的计算过程是
• 200×(80%+90%)=340
• 元，错误地将两次折扣的率相加，而实际应是连续相乘。
• 正确解答：衣服先打八折后的价格为
• 200×80%
• ，再在此基础上打九折，所以现价是
• 200×80%×90%=144
• 元。

二、圆柱与圆锥（空间想象能力不足，公式易混淆）

这部分内容主要涉及立体图形的表面积和体积计算，对学生的空间想象能力要求较高，而且相关公式较为相似，学生很容易出现记忆混淆、使用错误的情况。

1. 圆柱表面积计算：漏算或多算 “底面积”“侧面积”

在计算圆柱表面积时，学生常出现两种错误：一是计算 “无盖圆柱”（如日常使用的水桶）的表面积时，仍然错误地计算两个底面积；二是计算 “通风管”“烟囱” 这类特殊圆柱的表面积时，误加了底面积，实际上这类物体只需要计算侧面积即可。

• 错误案例：题目要求 “制作一个底面半径为 2cm、高为 5cm 的无盖圆柱水杯，需要多少平方厘米的铁皮？”，有学生的解答是表面积 = 侧面积 + 2 个底面积，即
• 2A
• ~
• 3.14A
• ~
• 2A
• ~
• 5+2A
• ~
• 3.14A
• ~
• 2A
• ^
• 2
• =87.92
• cm²，这里多算了一个底面积。
• 正确解答：无盖圆柱水杯的表面积只需计算侧面积加一个底面积，所以正确结果是
• 2A
• ~
• 3.14A
• ~
• 2A
• ~
• 5+3.14A
• ~
• 2A
• ^
• 2
• =62.8+12.56=75.36
• cm²。

2. 圆锥体积公式：漏乘 “1/3” 或混淆与圆柱体积关系

圆锥体积公式为

V=1/3Sh

，学生在计算时经常会忘记乘 “1/3”；同时，也容易忽略 “等底等高” 这个前提条件，直接表述 “圆锥体积是圆柱体积的 1/3”。

• 错误案例：已知 “一个圆锥的底面积是 12cm²、高是 3cm，求这个圆锥的体积是多少？”，部分学生的计算过程是
• V=12A
• ~
• 3=36
• cm³，遗漏了公式中的 “1/3”。
• 正确解答：根据圆锥体积公式，应计算为
• V=1/3A
• ~
• 12A
• ~
• 3=12
• cm³。

3. “等积变形” 问题：忽略形状变化中 “体积不变” 的关键

当遇到将圆柱熔铸成圆锥（或反过来将圆锥熔铸成圆柱）这类 “等积变形” 题目时，学生常常会错误地认为 “表面积不变”，实际上在形状变化过程中，体积始终保持不变，解题时需要利用 “体积相等” 这一关键条件建立等式。

• 错误案例：题目为 “一个圆柱的体积是 90cm³，将其熔铸成一个与它等底的圆锥，已知原来圆柱的高是 3cm，求熔铸后圆锥的高是多少？”，有些学生直接认为圆锥的高等于圆柱的高，即 3cm，忽略了体积相等时，等底的圆锥高是圆柱高的 3 倍这一关系。
• 正确解答：设圆柱和圆锥的底面积都为 S，圆柱体积公式为
• Sha
• ^
• =90
• （其中
• ha
• ^
• =3
• cm），圆锥体积公式为
• 1/3Sha
• ^
• =90
• ，由此可推出
• ha
• ^
• =3ha
• ^
• =3A
• ~
• 3=9
• cm。