如需全套各科电子课本PDF版（可下载打印）

请关注公众号“禾沐教辅网”（ ID: hemujiaofu ）

关注后自动获取资料合集（包含下列推荐资料）

500T学习资料分享

同步25年秋季学校教学进度持续更新.......

鲁教版六年级下册数学电子课本的目录如下：

第五章 基本平面图形

线段、射线、直线

比较线段的长短

角

角的比较

多边形和圆的初步认识

回顾与思考

第六章 整式的乘除

同底数幂的乘法

幂的乘方与积的乘方

同底数幂的除法

零指数幂与负整数指数幂

整式的乘法

平方差公式

完全平方公式

整式的除法

回顾与思考

综合与实践：设计自己的运算程序

第七章 相交线与平行线

两条直线的位置关系

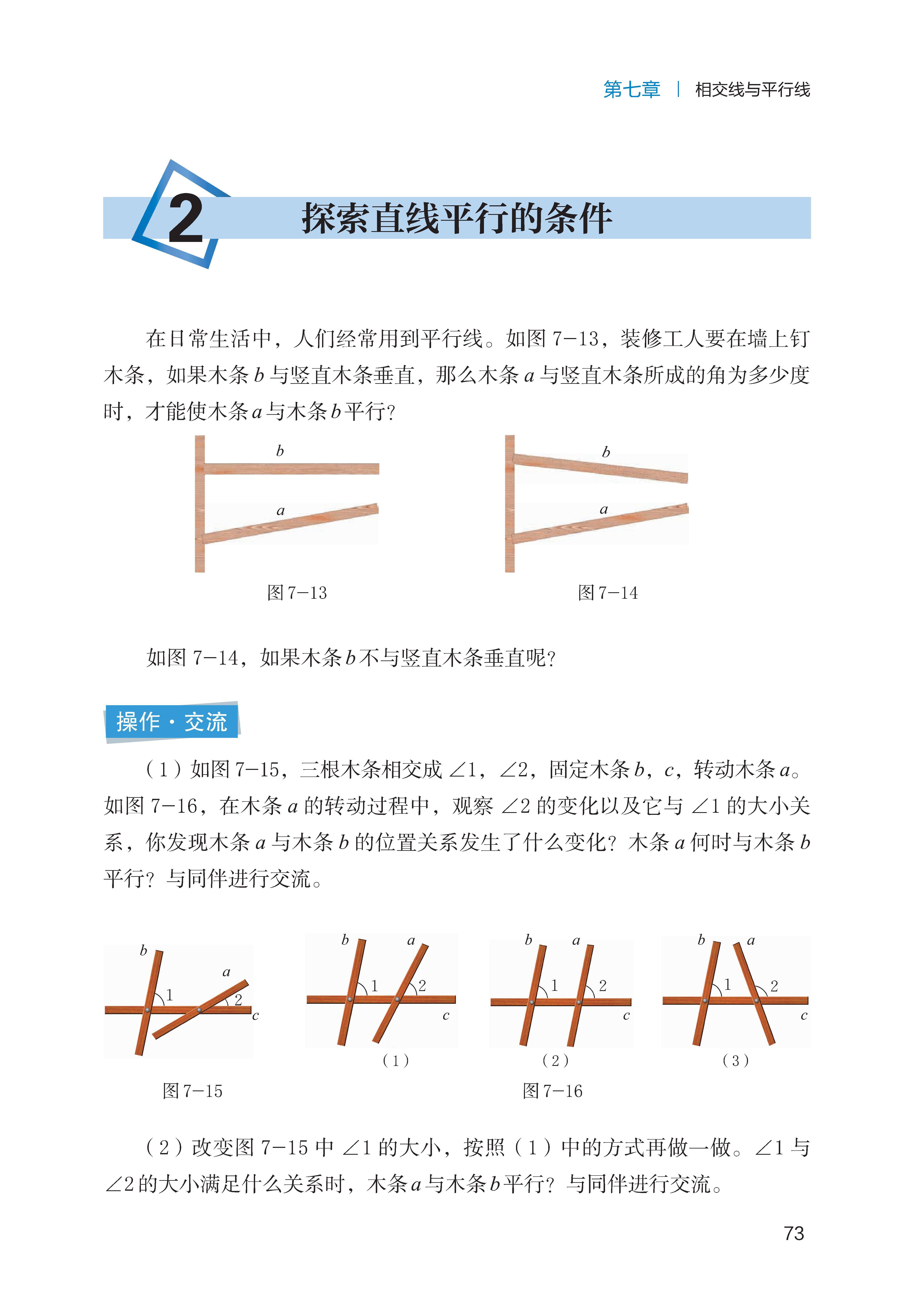
探索直线平行的条件

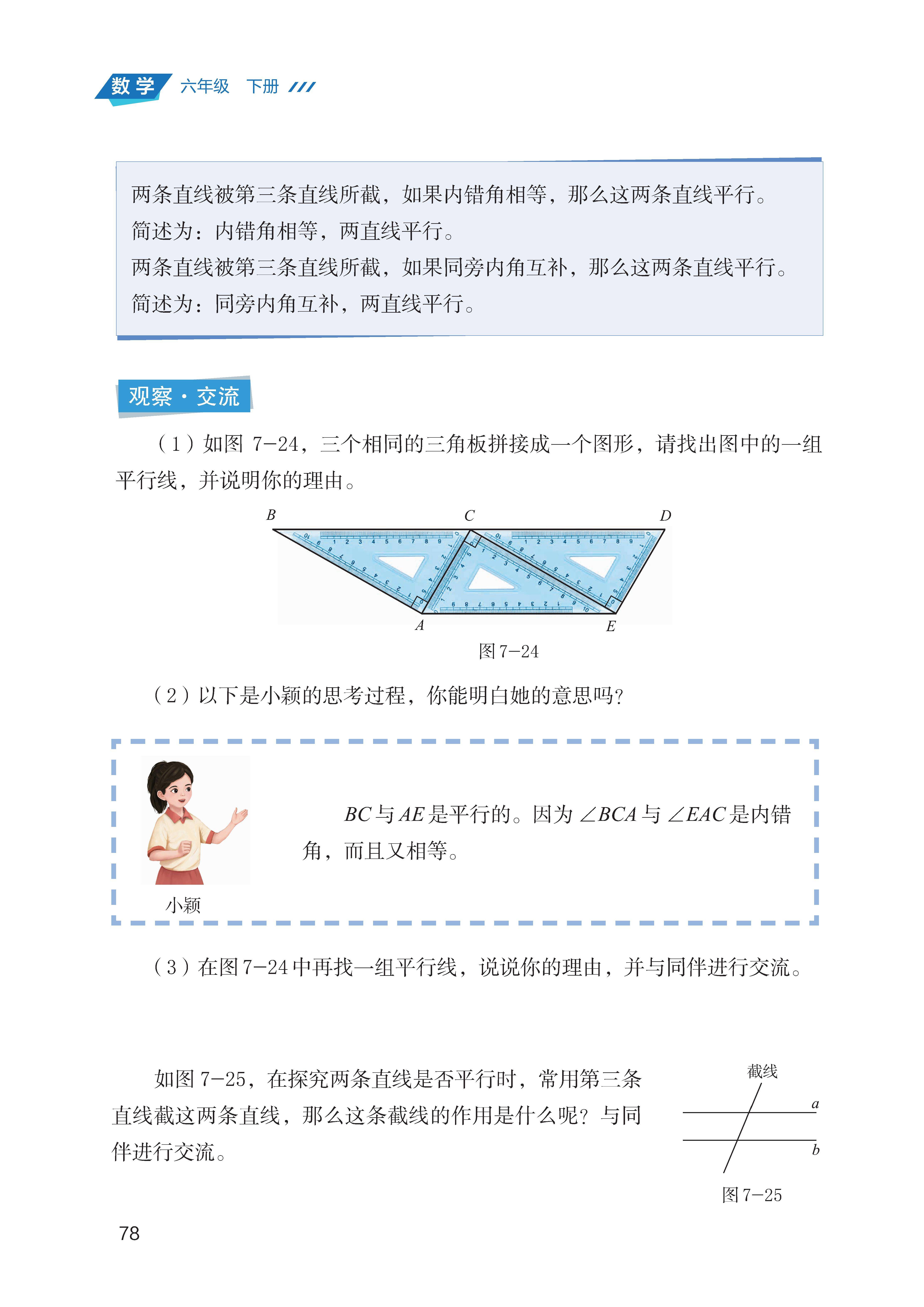
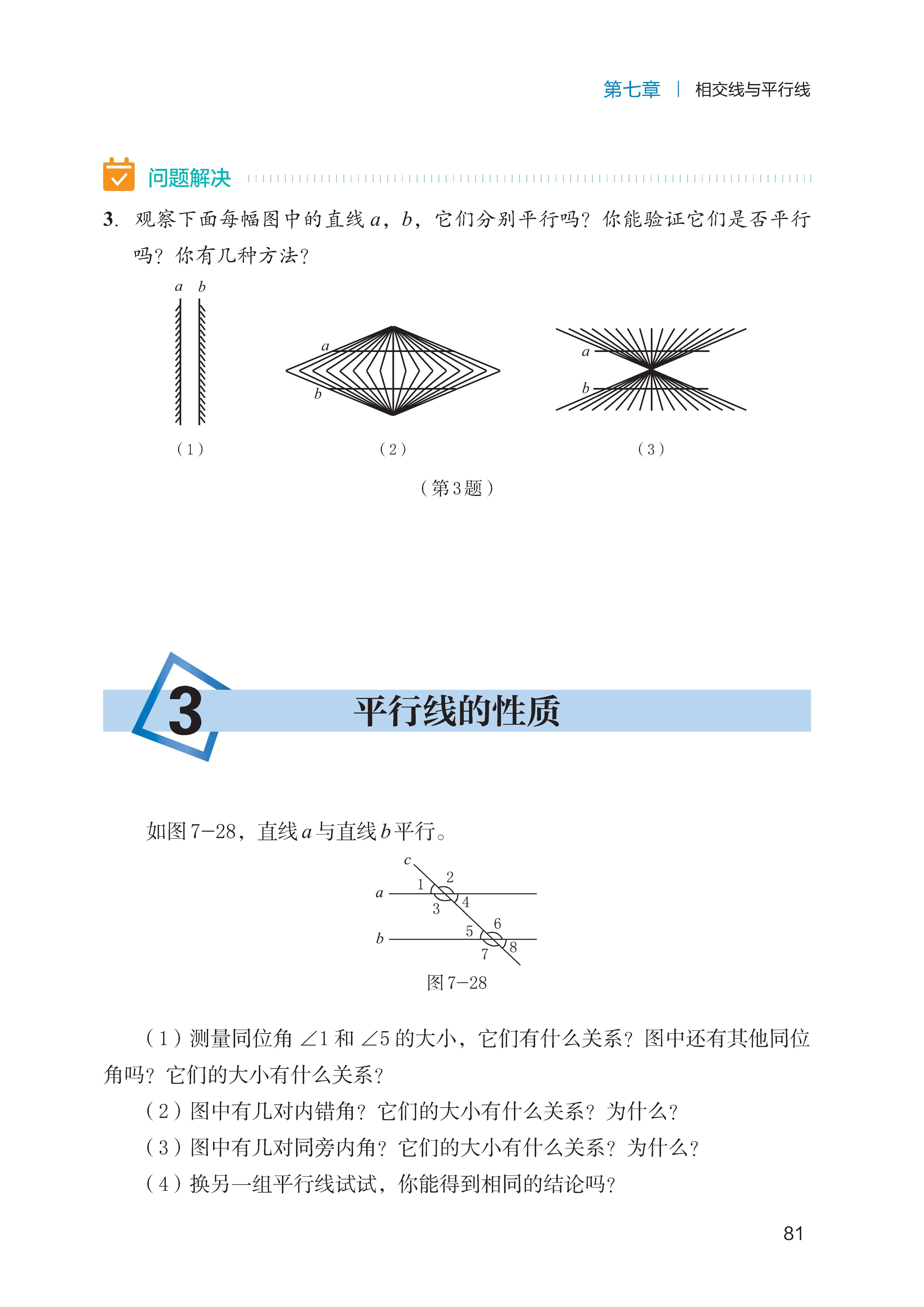
平行线的性质

用尺规作角

回顾与思考

第八章 数据的收集与整理

数据的收集

普查和抽样调查

数据的表示

统计图的选择

回顾与思考

综合与实践：关注人口老龄化

第九章 变量之间的关系

用表格表示变量之间的关系

用表达式表示变量之间的关系

用图象表示变量之间的关系

回顾与思考

鲁教版六年级下册数学课本目录包含五章核心内容，各章节的学习重点和难点明确，既承接上册知识，又为初中后续数学学习奠定基础。以下是分章节的详细梳理：

第五章 基本平面图形

学习重点

核心概念的理解与区分：明确线段、射线、直线的定义及区别（如端点数量、延伸性），掌握角的定义（静态：由公共端点的两条射线组成；动态：一条射线绕端点旋转形成）、表示方法（用三个字母、一个字母或数字表示）。

图形的度量与比较：

会用刻度尺测量线段长度，能借助圆规或叠合法比较线段长短，理解 “两点之间线段最短” 的基本事实。

会用量角器测量角的度数，能通过叠合法或度量法比较角的大小，掌握角的单位换算（1°=60′，1′=60″）。

基础图形的认知：认识多边形（从边数区分三角形、四边形、五边形等）的定义，了解圆的基本元素（圆心、半径、直径、弧、扇形）。

学习难点

射线、直线的 “无限延伸性” 理解：小学阶段接触的图形多为有限长度，初中首次接触 “无限延伸” 的射线和直线，容易因具象思维局限，难以准确理解其特性（如 “过两点有且只有一条直线” 的唯一性）。

角的动态定义与实际应用：部分学生对 “射线旋转形成角” 的动态过程理解困难，尤其在判断生活中 “旋转形成的角”（如时钟指针夹角）时，容易忽略旋转方向和范围。

第六章 整式的乘除

学习重点

幂的运算规律：熟练掌握同底数幂的乘法（

a

m

⋅a

n

=a

m+n

）、幂的乘方（

(a

m

)

n

=a

mn

）、积的乘方（

(ab)

n

=a

n

b

n

）、同底数幂的除法（

a

m

÷a

n

=a

m−n

，

a



=0

），并能灵活运用（如逆用公式简化计算）。

特殊指数幂的意义：理解零指数幂（

a

0

=1

，

a



=0

）和负整数指数幂（

a

−n

=

a

n

1

，

a



=0

）的定义，避免与 “负数的幂” 混淆。

整式的乘除运算：

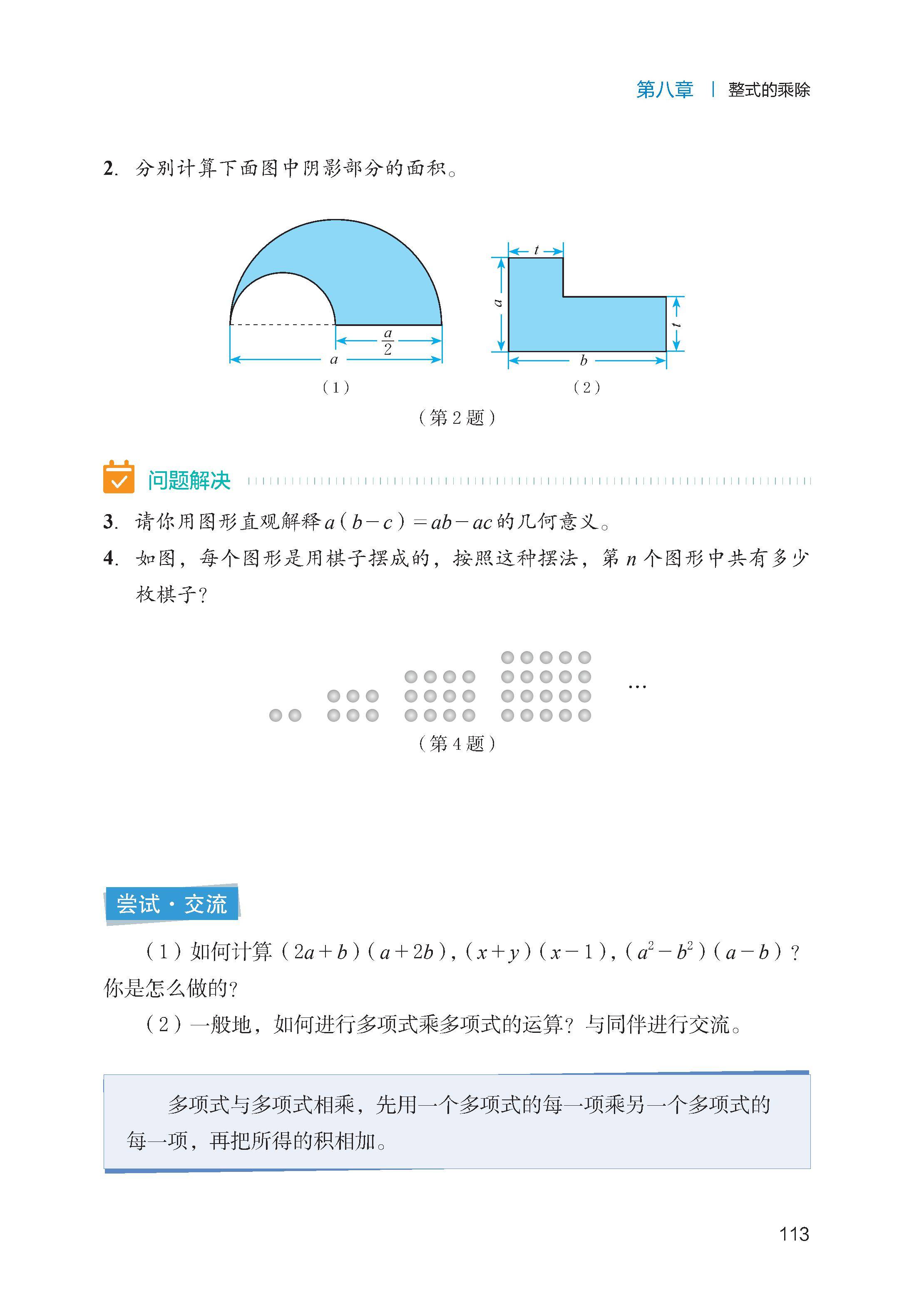
整式乘法：掌握单项式 × 单项式、单项式 × 多项式（分配律）、多项式 × 多项式（展开后合并同类项）的法则。

乘法公式：熟练运用平方差公式（

(a+b)(a−b)=a

2

−b

2

）和完全平方公式（

(a±b)

2

=a

2

±2ab+b

2

），能识别公式适用的结构（如 “两项和 × 两项差” 用平方差，“两项和 / 差的平方” 用完全平方）。

整式除法：掌握单项式 ÷ 单项式、多项式 ÷ 单项式（分配律）的法则。

学习难点

幂的运算公式的逆用与符号处理：

逆用公式（如

a

m+n

=a

m

⋅a

n

）时，容易忽略指数的关系；

涉及负数或字母符号时（如

(−a)

2

与

−a

2

的区别），容易混淆符号结果。

乘法公式的灵活应用：

完全平方公式中 “中间项

±2ab

” 的符号和系数容易遗漏（如

(a−b)

2

误写成

a

2

−b

2

）；

对 “变形后符合公式” 的式子（如

(2x+3y)(−2x+3y)

可转化为

(3y+2x)(3y−2x)

用平方差），难以快速识别结构。

多项式 × 多项式的展开与合并同类项：项数较多时（如三项式 × 三项式），容易漏乘某一项或合并同类项出错。

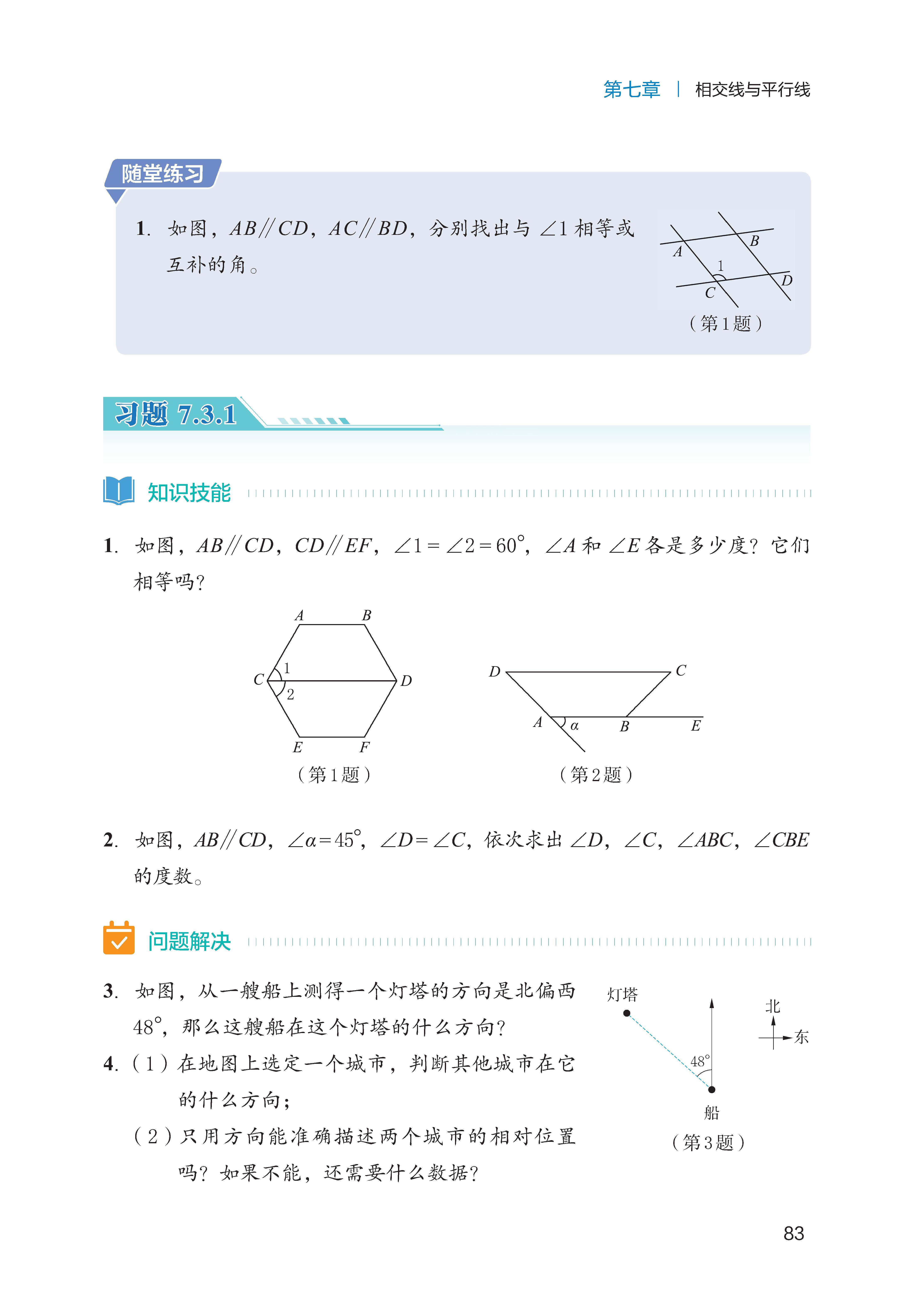
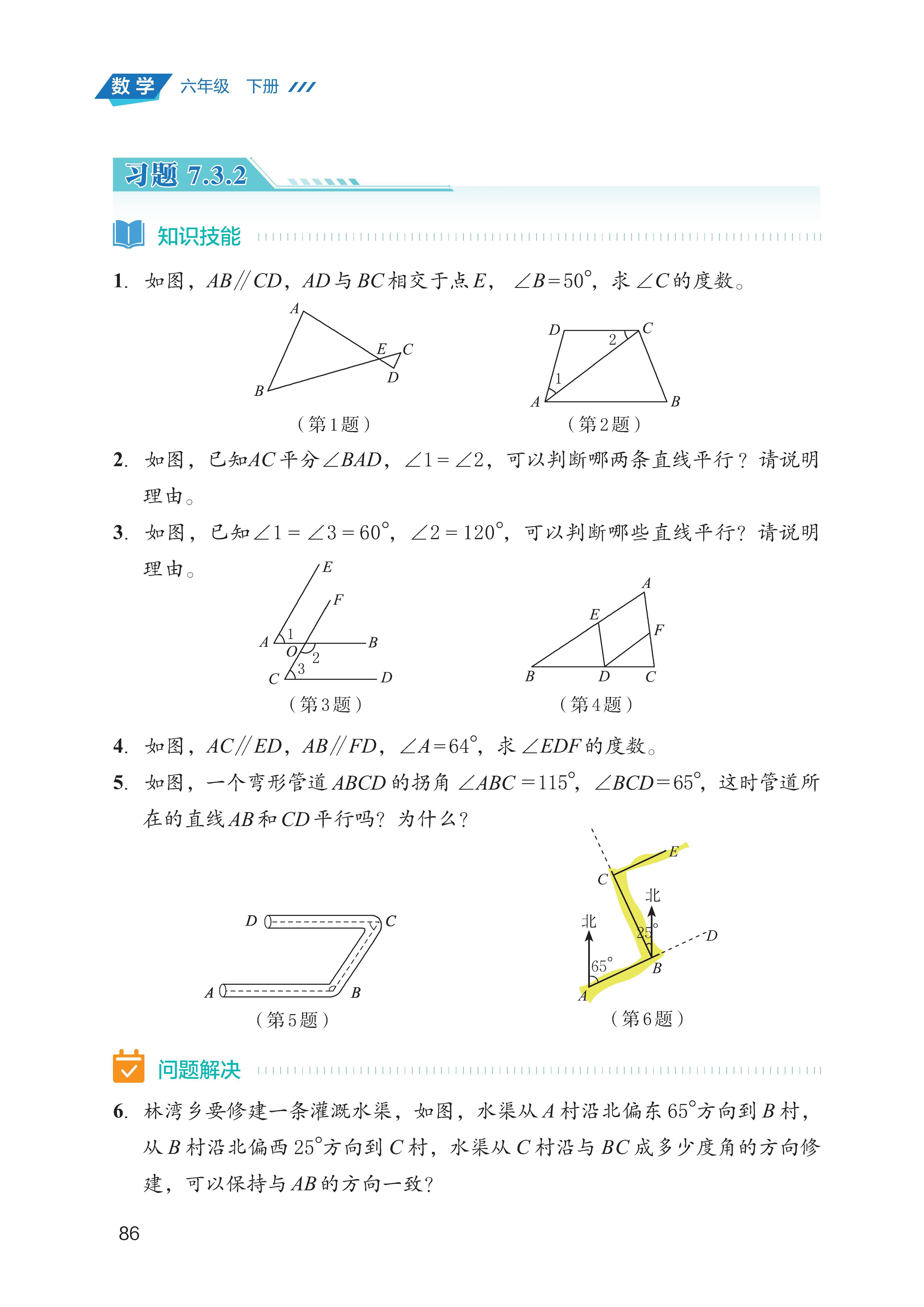
第七章 相交线与平行线

学习重点

相交线的核心概念：认识对顶角（相等）、邻补角（和为 180°），掌握垂直的定义（两条直线相交成 90°）、性质（过一点有且只有一条直线与已知直线垂直）及点到直线的距离（垂线段最短）。

平行线的判定与性质：

判定：能根据 “同位角相等”“内错角相等”“同旁内角互补”，判断两条直线平行；

性质：已知两条直线平行，能推出 “同位角相等”“内错角相等”“同旁内角互补”；

明确 “判定”（由角的关系推线平行）与 “性质”（由线平行推角的关系）的逻辑区别。

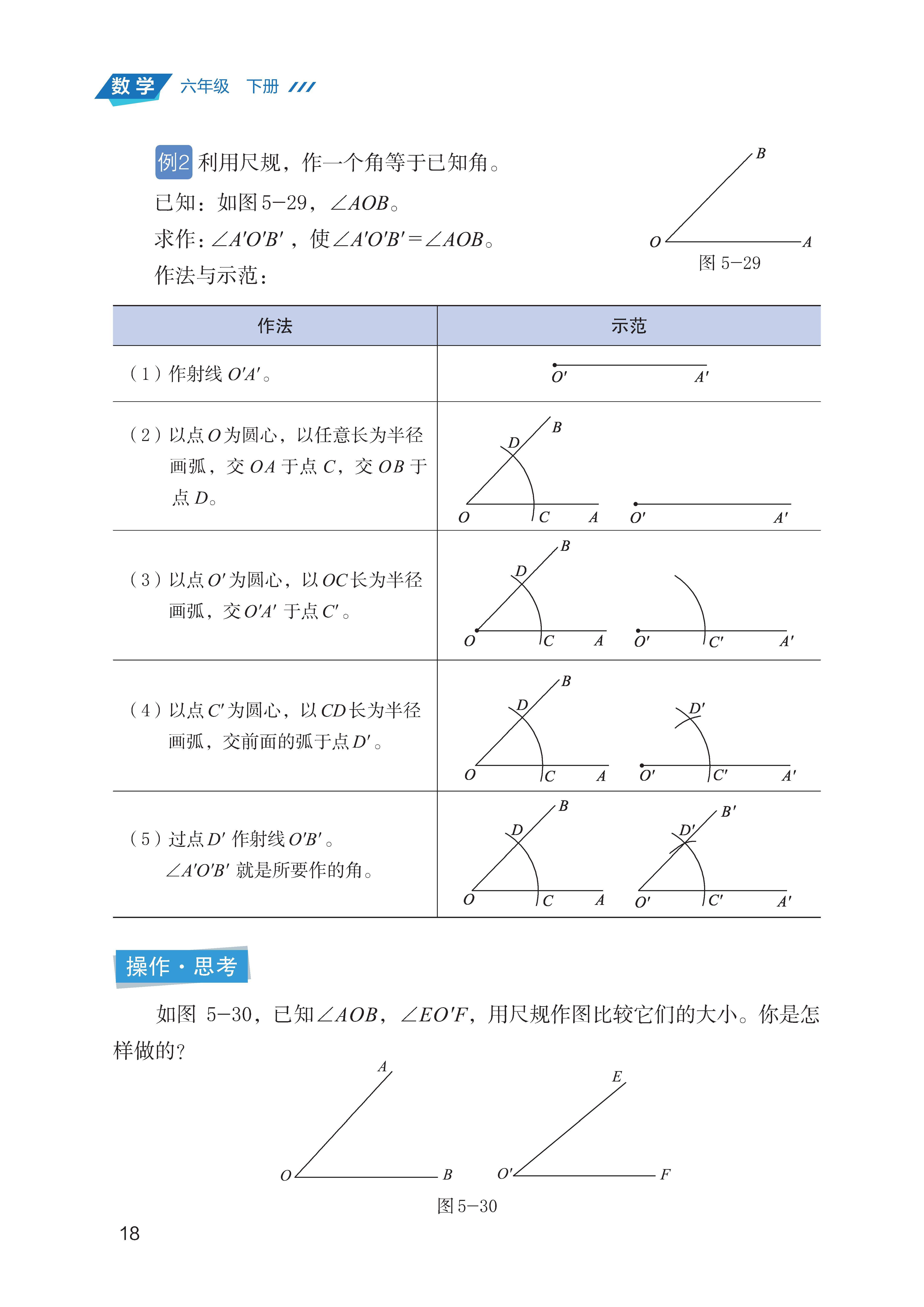
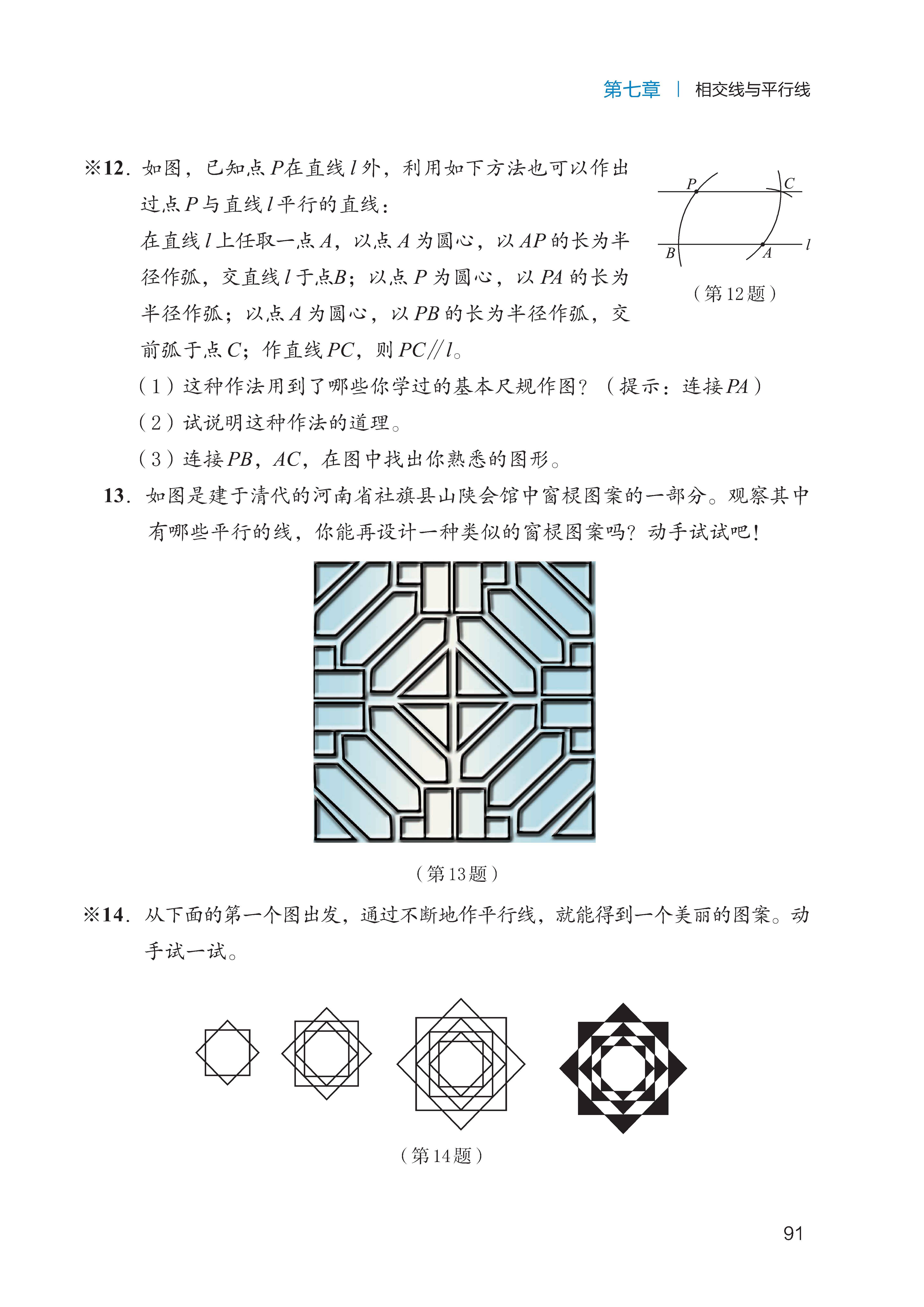
尺规作图：掌握用尺规 “作一个角等于已知角” 的步骤（定圆心、画弧、找交点），理解作图的依据（全等三角形的判定）。

学习难点

平行线判定与性质的混合运用：在复杂图形（如多条直线相交、含辅助线）中，难以快速识别 “同位角、内错角、同旁内角”，且容易混淆 “判定” 和 “性质” 的逻辑顺序（如用 “线平行” 推 “角相等” 时，误写为判定依据）。

“点到直线的距离” 与 “垂线段” 的区别：容易将 “垂线段”（图形）与 “点到直线的距离”（垂线段的长度，数量）混淆，如描述时误说 “垂线段是点到直线的距离”。

尺规作图的逻辑理解：部分学生仅记住 “步骤”，但不理解 “为什么这样作图能得到等角”（依据弧长相等即半径相等，构造全等三角形），导致作图后无法验证正确性。

第八章 数据的收集与整理

学习重点

数据收集的方法：明确 “普查”（对全体对象调查，如人口普查，结果准确但范围大、成本高）和 “抽样调查”（对部分对象调查，如抽查产品质量，范围小、效率高但有误差）的适用场景，能根据问题选择合适的调查方式。

数据的表示与统计图选择：

掌握条形统计图（直观比较不同类别数据的数量）、折线统计图（反映数据的变化趋势）、扇形统计图（表示各部分占总体的百分比）的特点；

能根据数据需求选择合适的统计图（如 “比较不同班级的人数” 用条形图，“看一周气温变化” 用折线图，“看各科目成绩占总分的比例” 用扇形图）。

数据的分析基础：能从统计图中提取关键信息（如最大值、最小值、百分比、变化趋势），并进行简单解读（如 “扇形图中某部分占比 30%，表示该部分占总体的 3/10”）。

学习难点

抽样调查的 “样本代表性” 理解：难以判断样本是否合理（如调查全校学生身高，仅抽样一年级学生则样本不具代表性），容易忽略 “样本需随机、均匀” 的原则。

扇形统计图的计算与绘制：

计算某部分对应的圆心角（圆心角 = 360°× 该部分占比）时，容易出错；

绘制时难以准确分配各部分的扇形面积，尤其当占比接近时。

多统计图的综合解读：面对同一组数据的不同统计图（如条形图 + 折线图），难以整合信息进行全面分析（如 “从条形图看数量，从折线图看变化，结合得出结论”）。

第九章 变量之间的关系

学习重点

变量的概念理解：明确 “变量”（变化的量，如时间、温度）和 “常量”（不变的量，如速度不变时的速度），能区分 “自变量”（主动变化的量，如时间）和 “因变量”（随自变量变化的量，如路程）。

变量关系的三种表示方法：

表格：能从表格中读取自变量与因变量的对应值，发现变化规律（如 “时间每增加 1 小时，路程增加 60 千米”）；

表达式：能根据实际问题列出因变量关于自变量的表达式（如路程

s=60t

，其中

t

是时间），并代入求值；

图象：能识别图象的横纵轴（分别对应自变量、因变量），从图象中读取信息（如 “图象上某点的横坐标是 2，纵坐标是 120，表示时间 2 小时时路程 120 千米”），理解图象的趋势（上升表示因变量随自变量增大而增大，下降则相反）。

学习难点

图象的解读与实际意义关联：

容易混淆横纵轴对应的变量（如误将 “纵轴当自变量，横轴当因变量”）；

对图象中 “水平线段”（表示因变量不变，如 “图象水平段表示时间增加但路程不变，即物体静止”）的实际意义理解困难。

从实际问题到表达式的转化：难以将文字描述转化为数学表达式（如 “一个长方形的长是 5cm，宽为

x

cm，面积

y

与

x

的关系”，需明确

y=5x

），容易忽略变量的取值范围（如宽

x>0

）。

三种表示方法的转化：如 “根据表格数据写出表达式”“根据表达式画出图象”，尤其当规律不明显（如非线性关系，如

y=x

2

）时，转化难度较大。