如需全套各科电子课本PDF版（可下载打印）

请关注公众号“禾沐教辅网”（ ID: hemujiaofu ）

关注后自动获取资料合集（包含下列推荐资料）

500T学习资料分享

同步25年秋季学校教学进度持续更新.......

鲁教版八年级下册数学电子课本的目录如下：

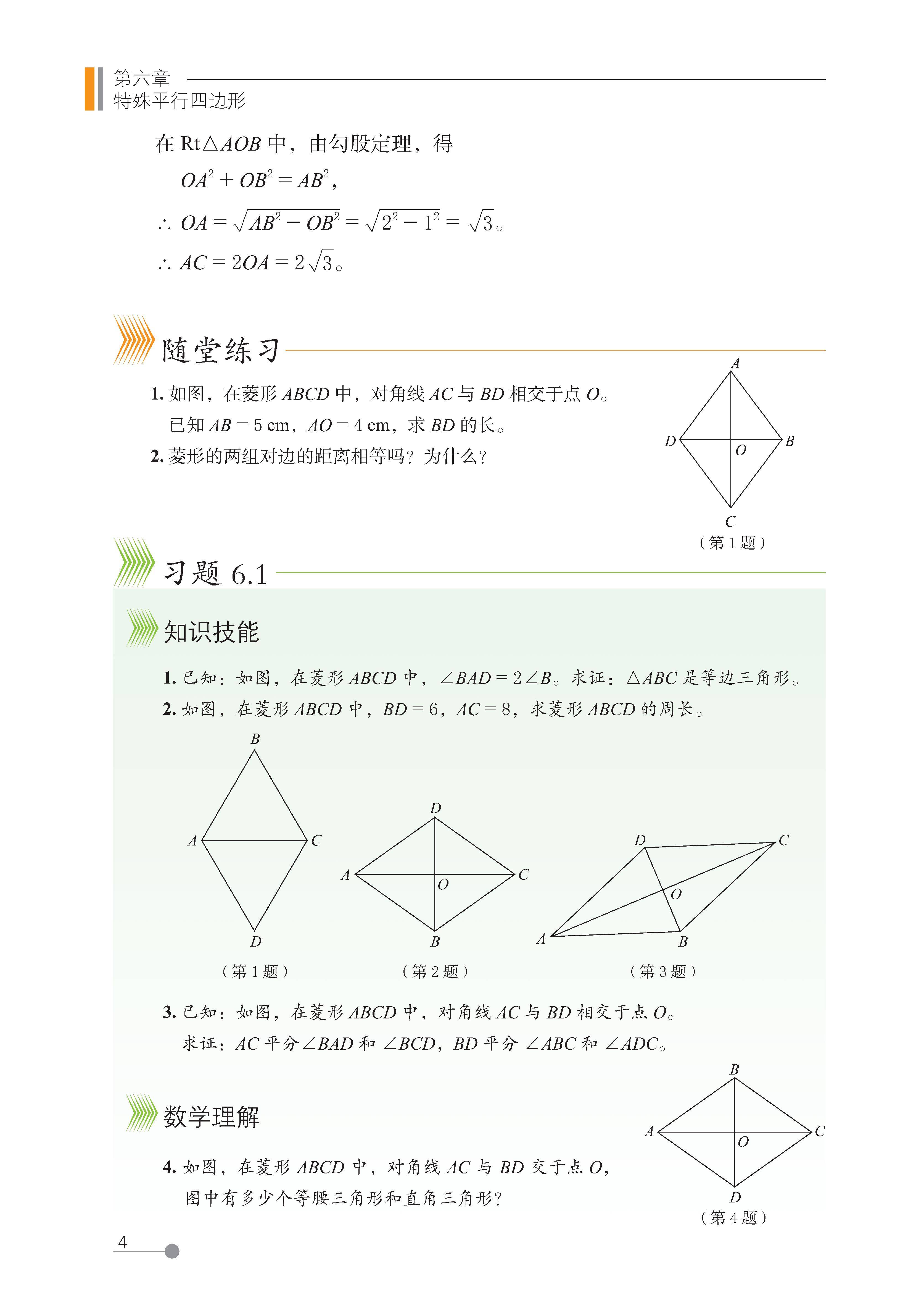
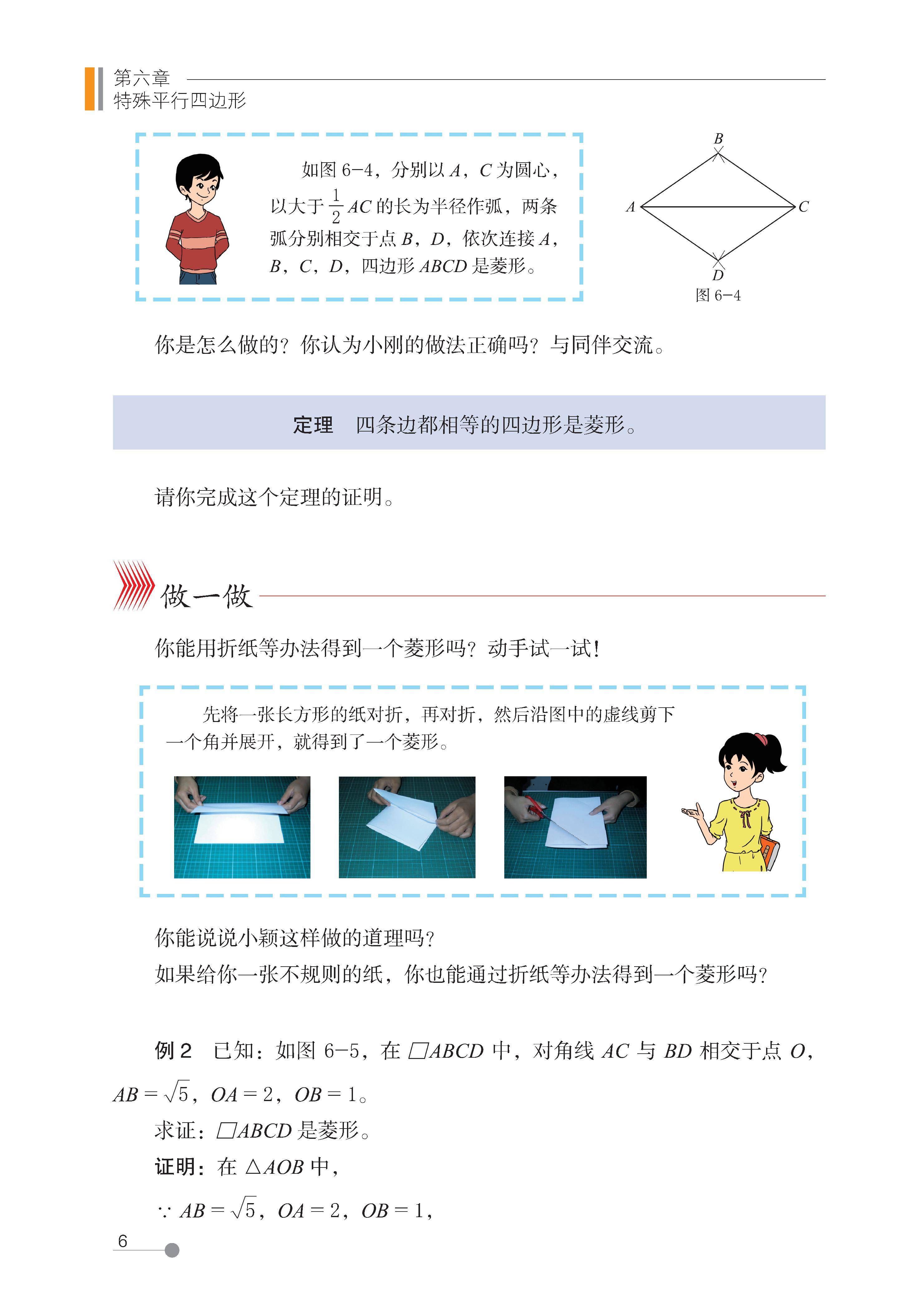
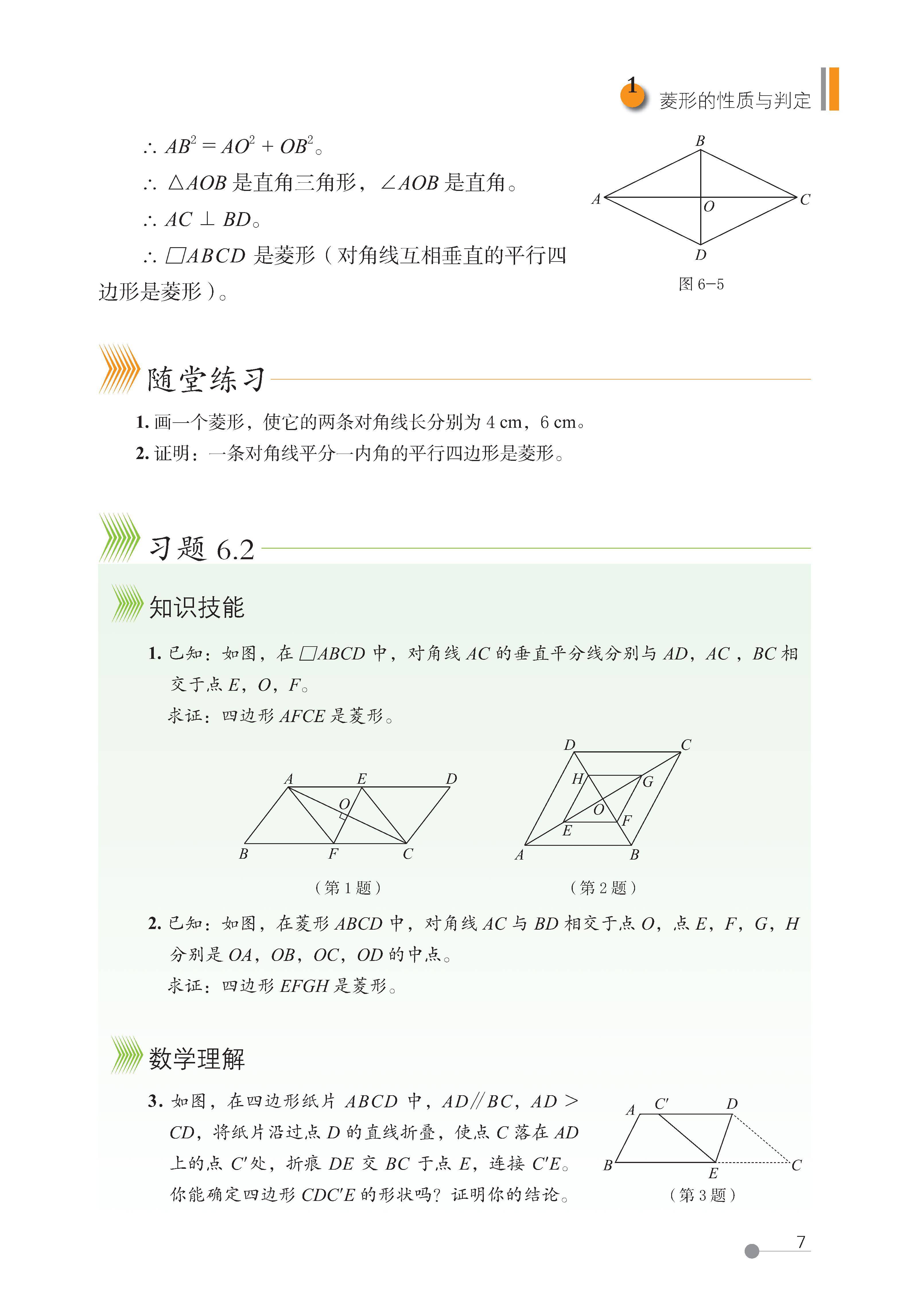
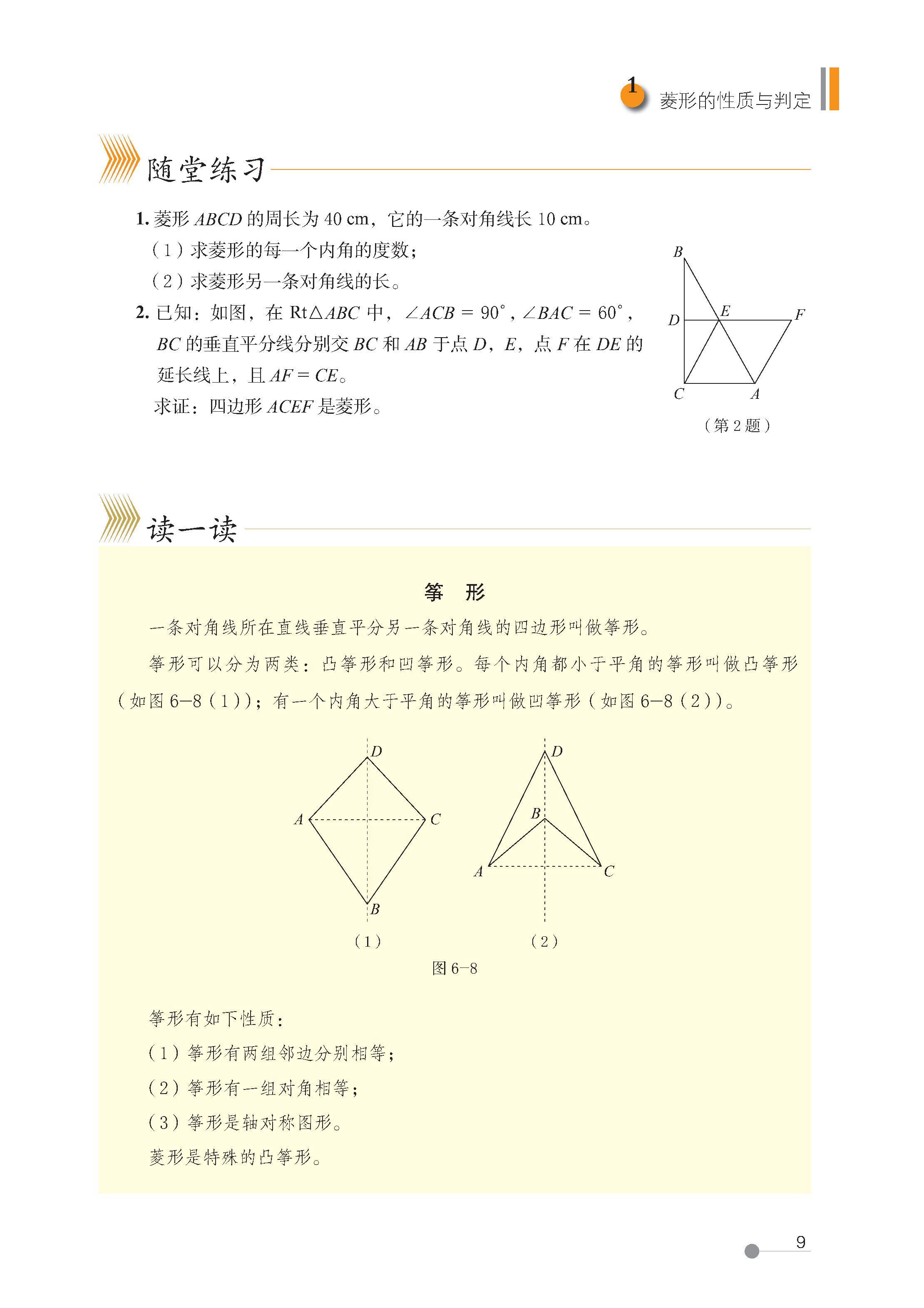
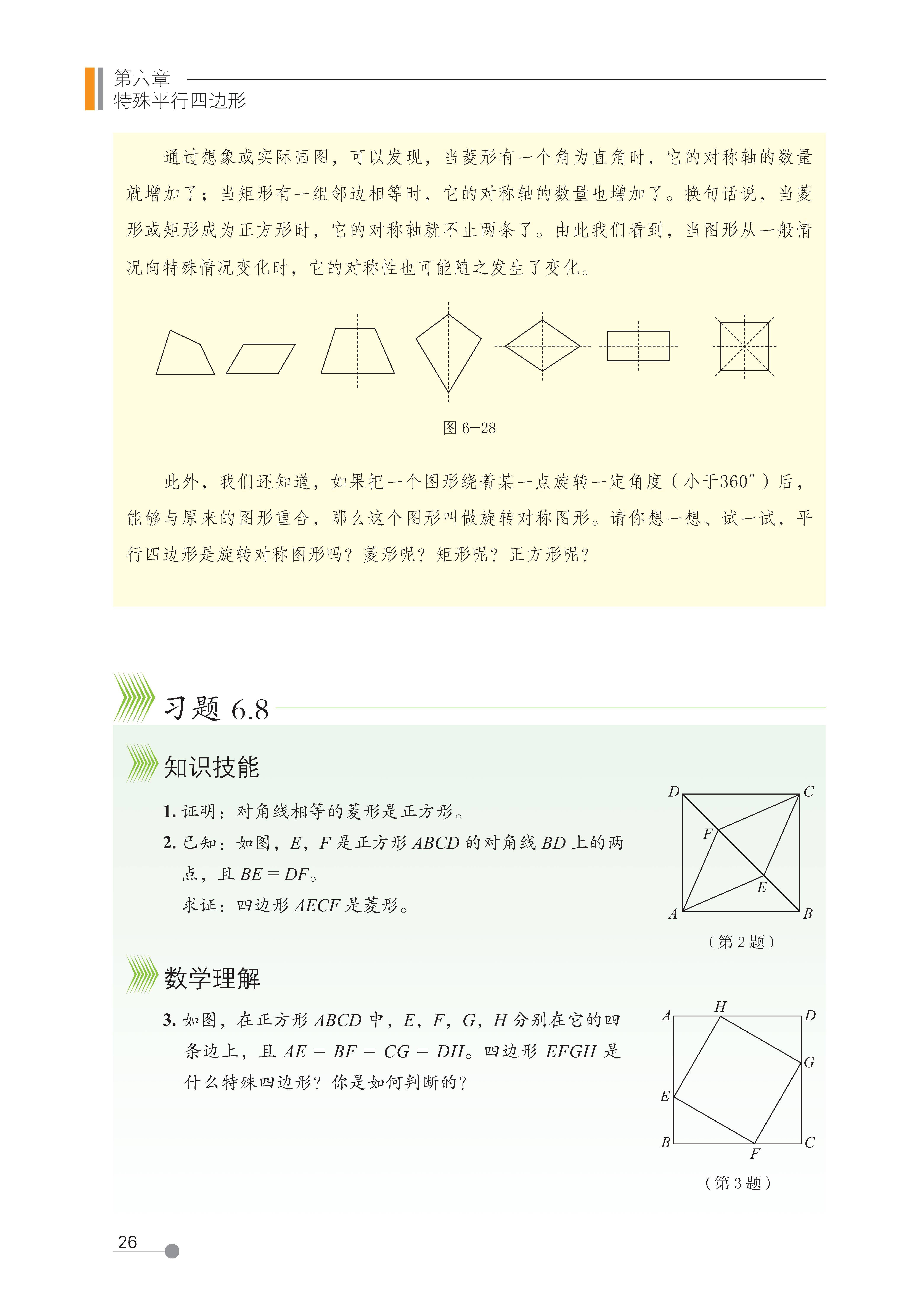
第六章 特殊平行四边形

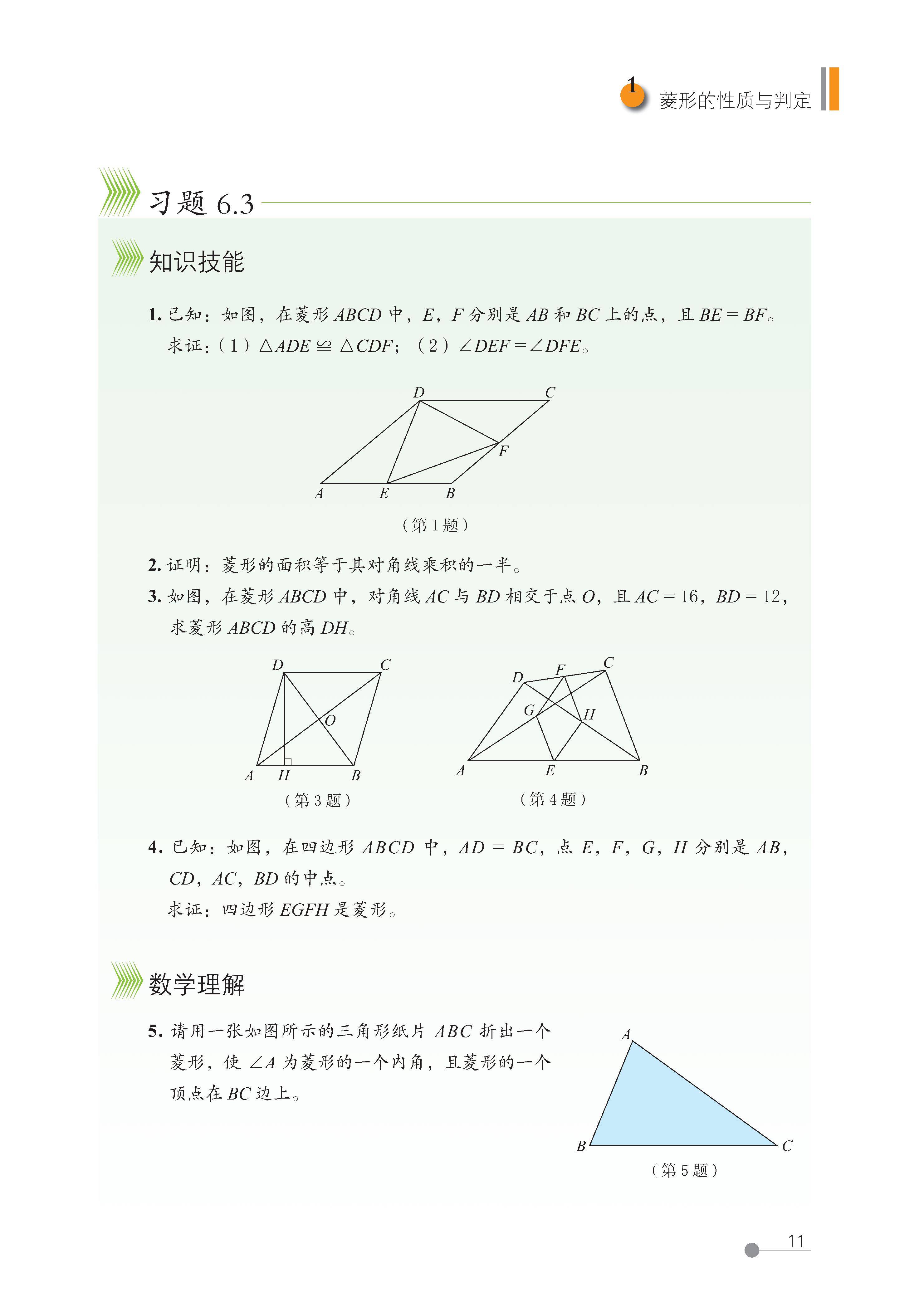
1 菱形的性质与判定

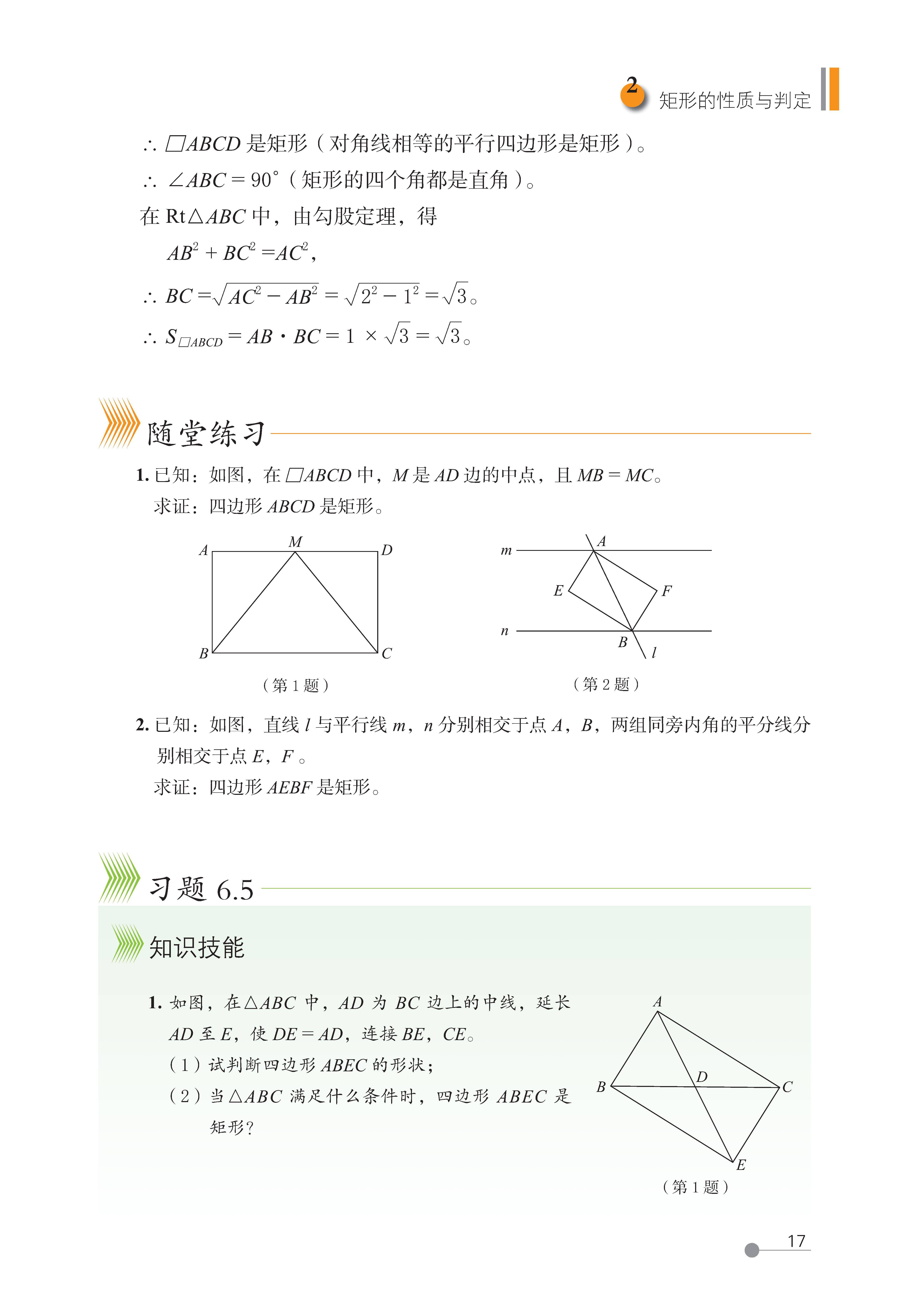
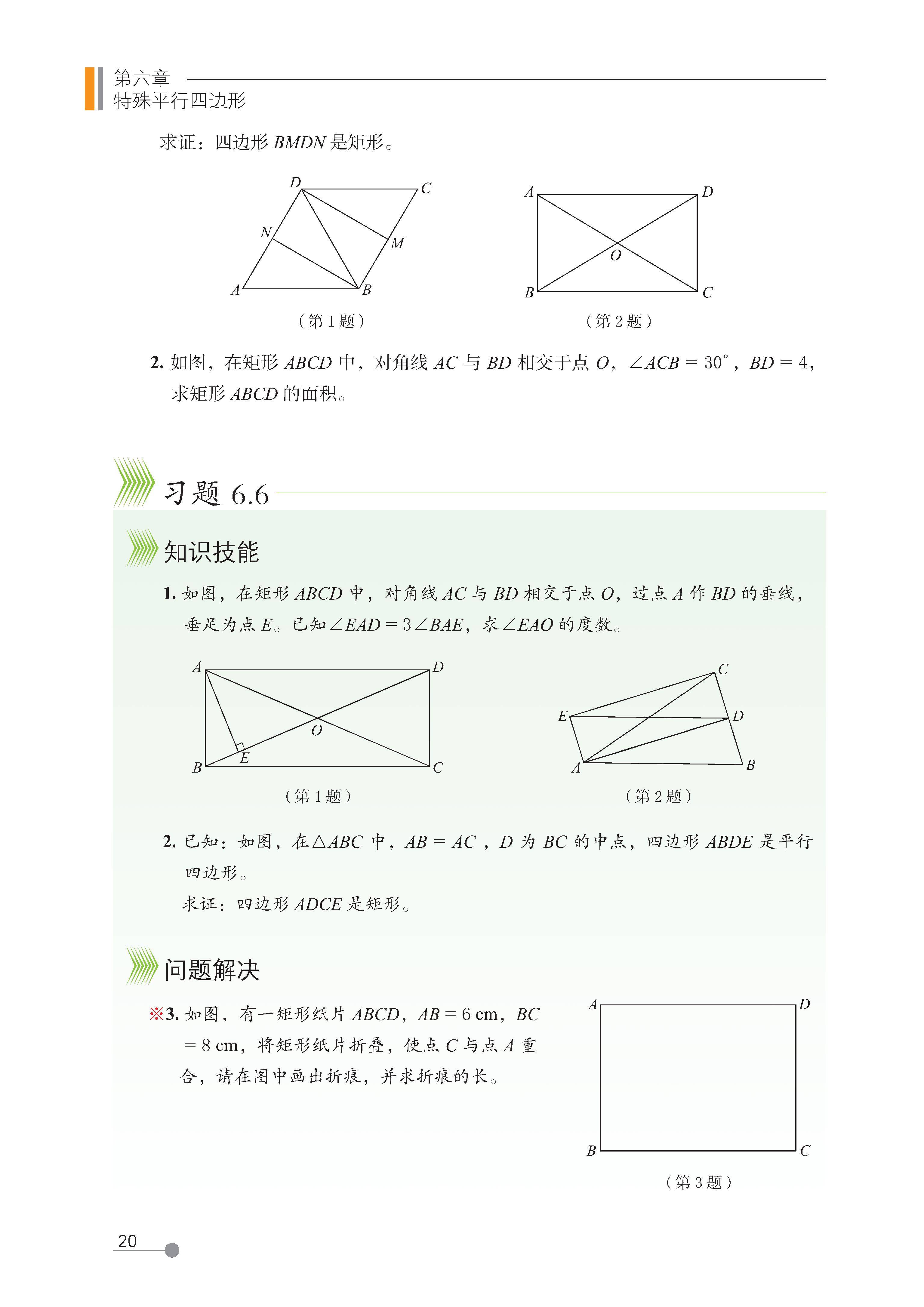
2 矩形的性质与判定

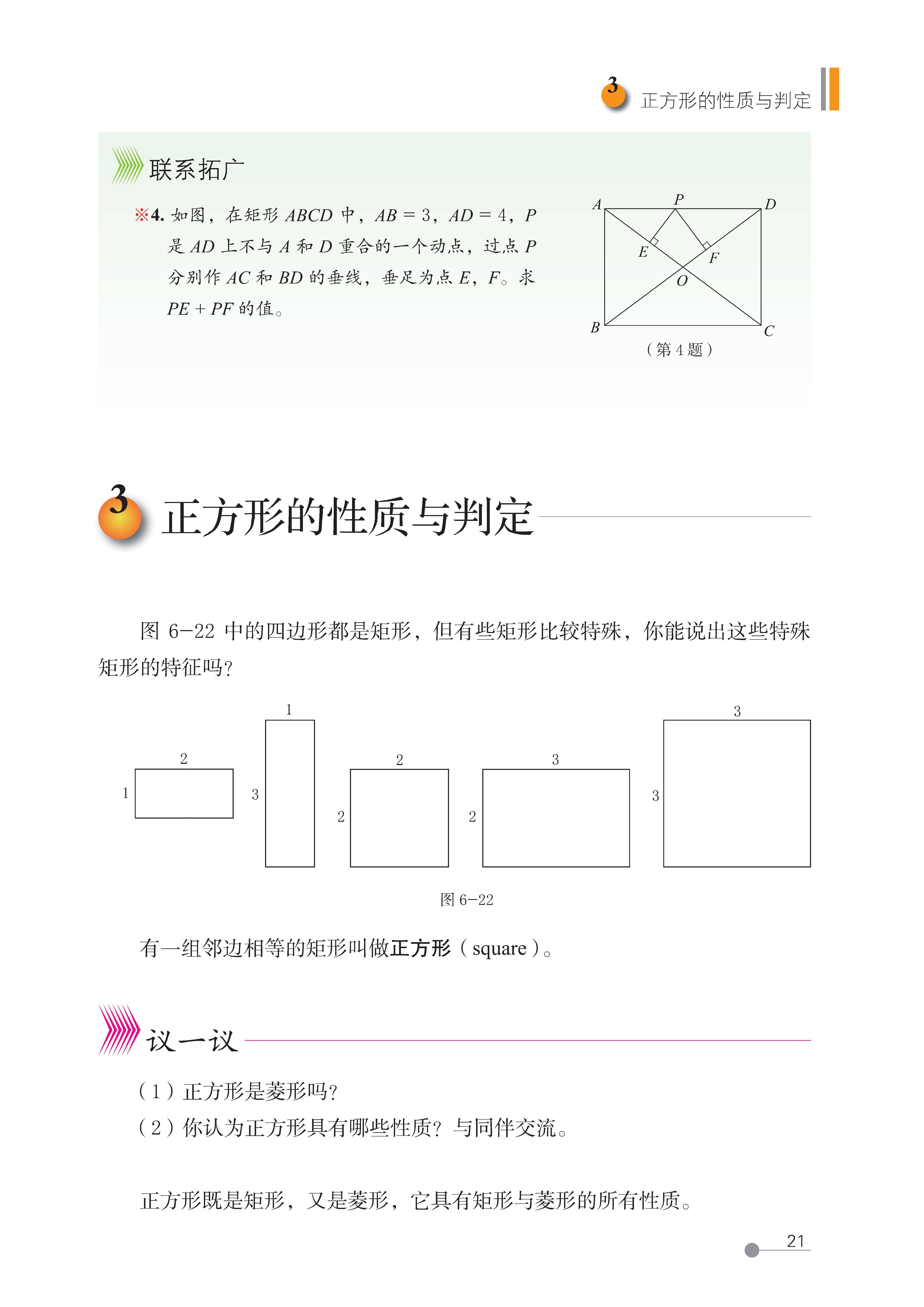
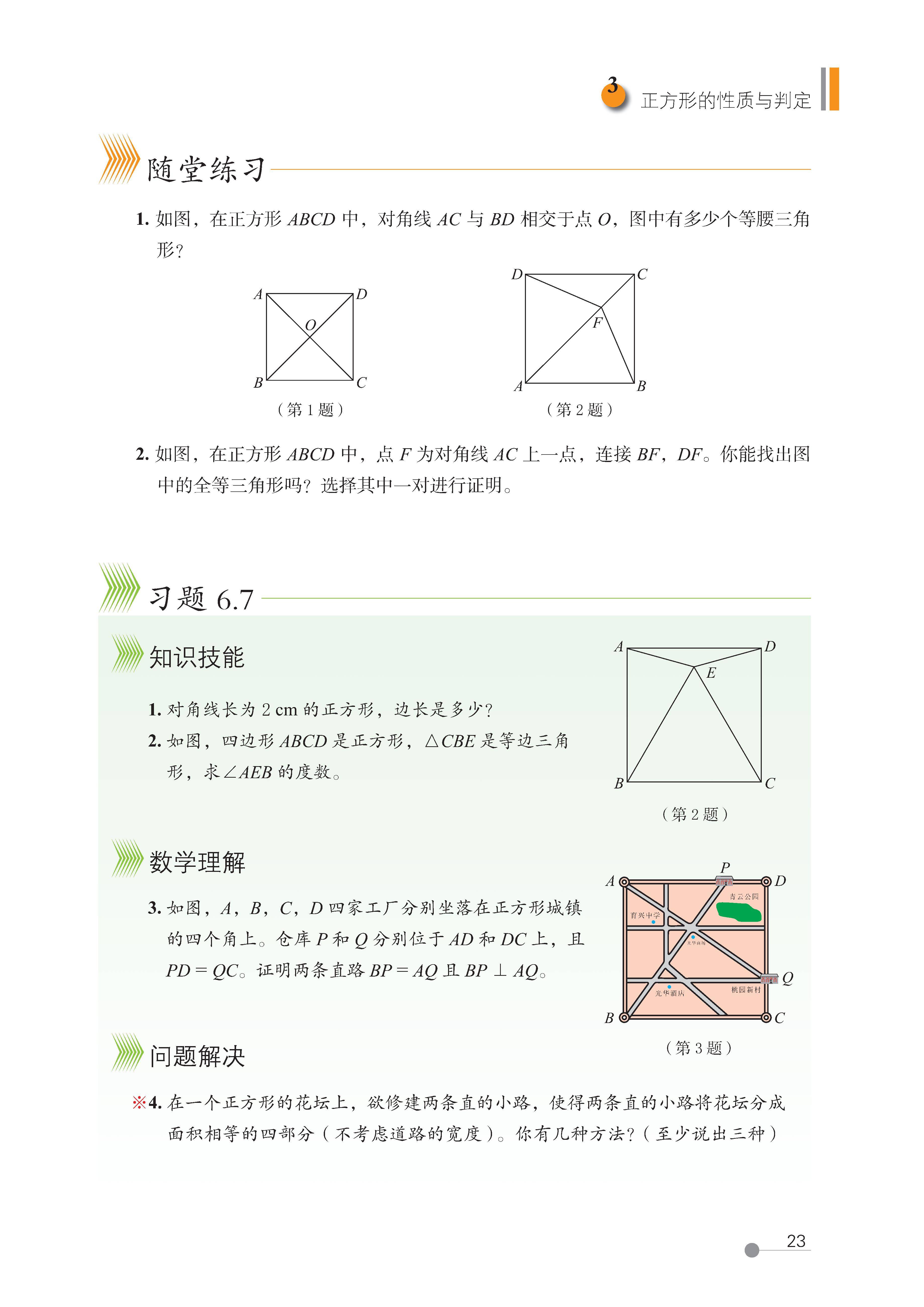
3 正方形的性质与判定

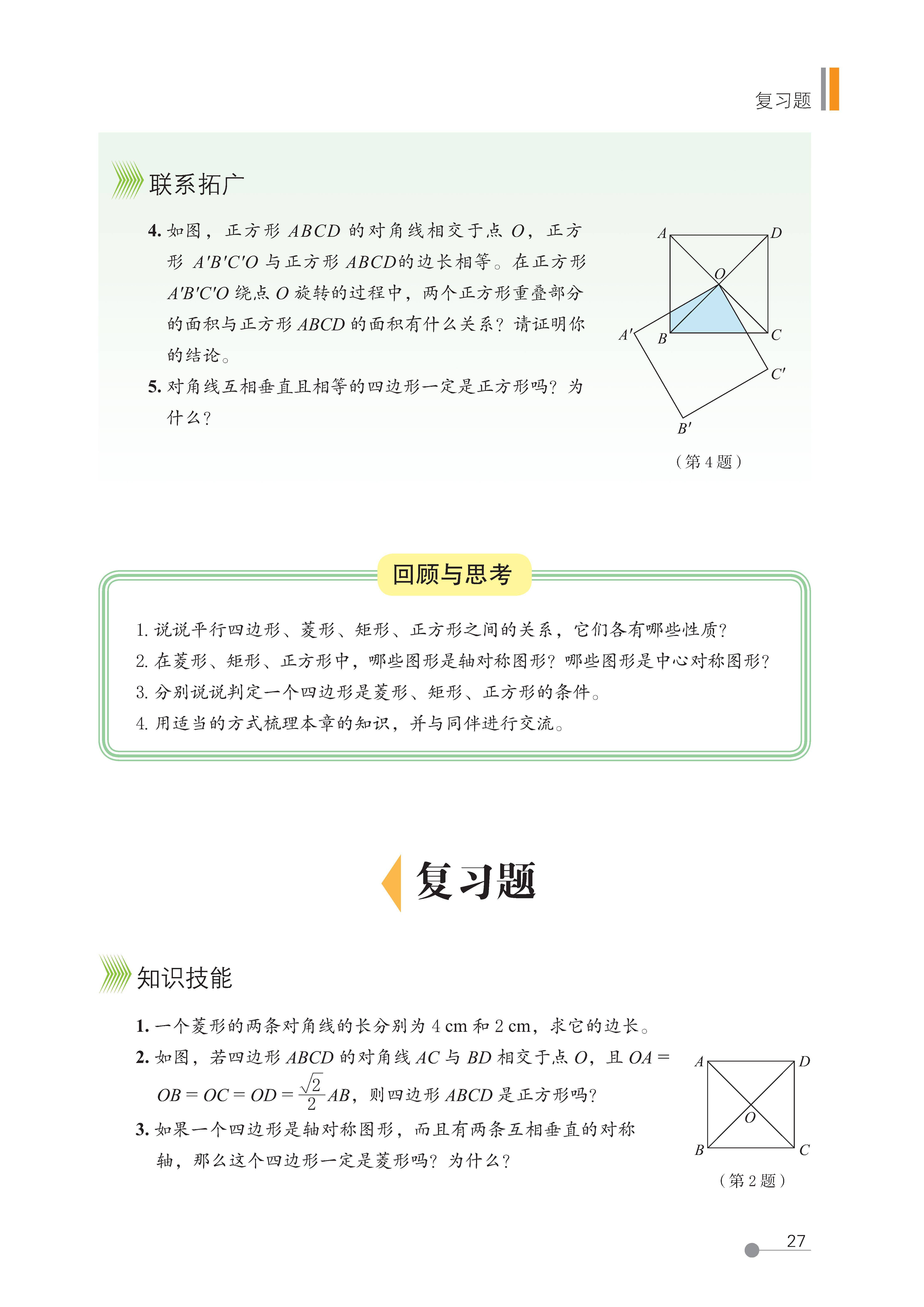
回顾与思考

复习题

第七章 二次根式

1 二次根式

2 二次根式的性质

3 二次根式的加减

4 二次根式的乘除

回顾与思考

复习题

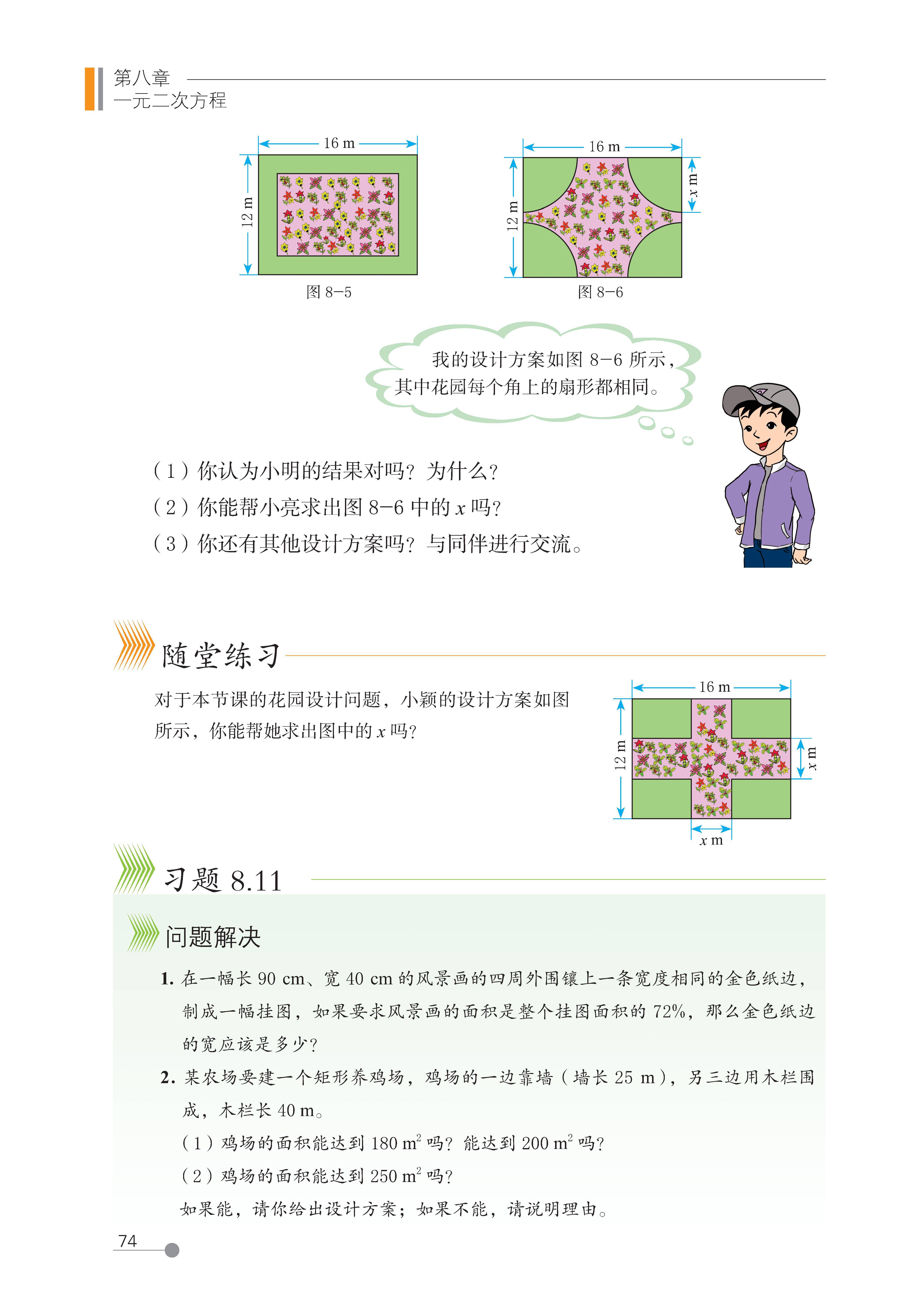
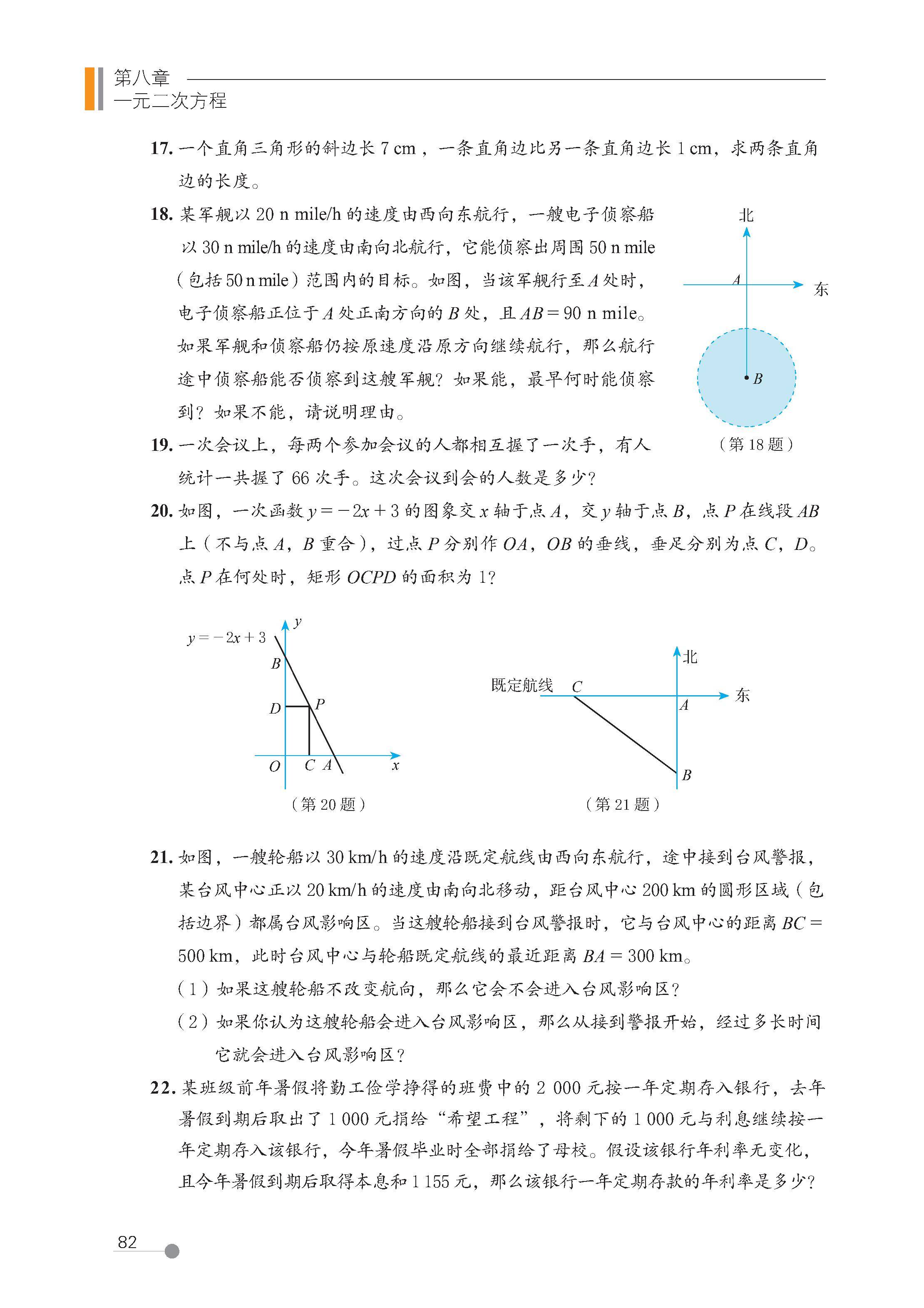
第八章 一元二次方程

1 一元二次方程

2 用配方法解一元二次方程

3 用公式法解一元二次方程

4 用分解因式法解一元二次方程

5 一元二次方程根与系数的关系

6 一元二次方程的应用

回顾与思考

复习题

第九章 图形的相似

1 成比例线段

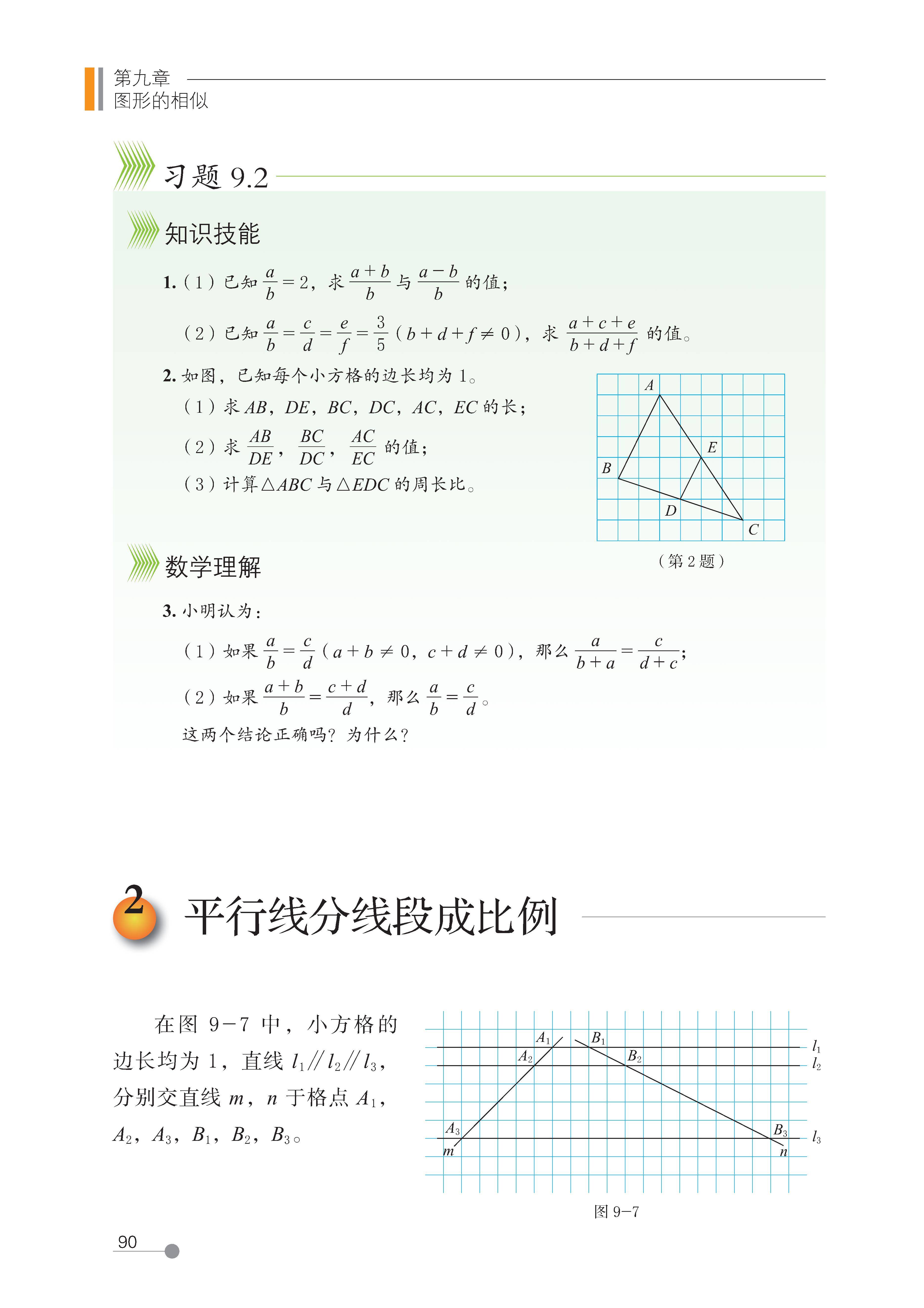
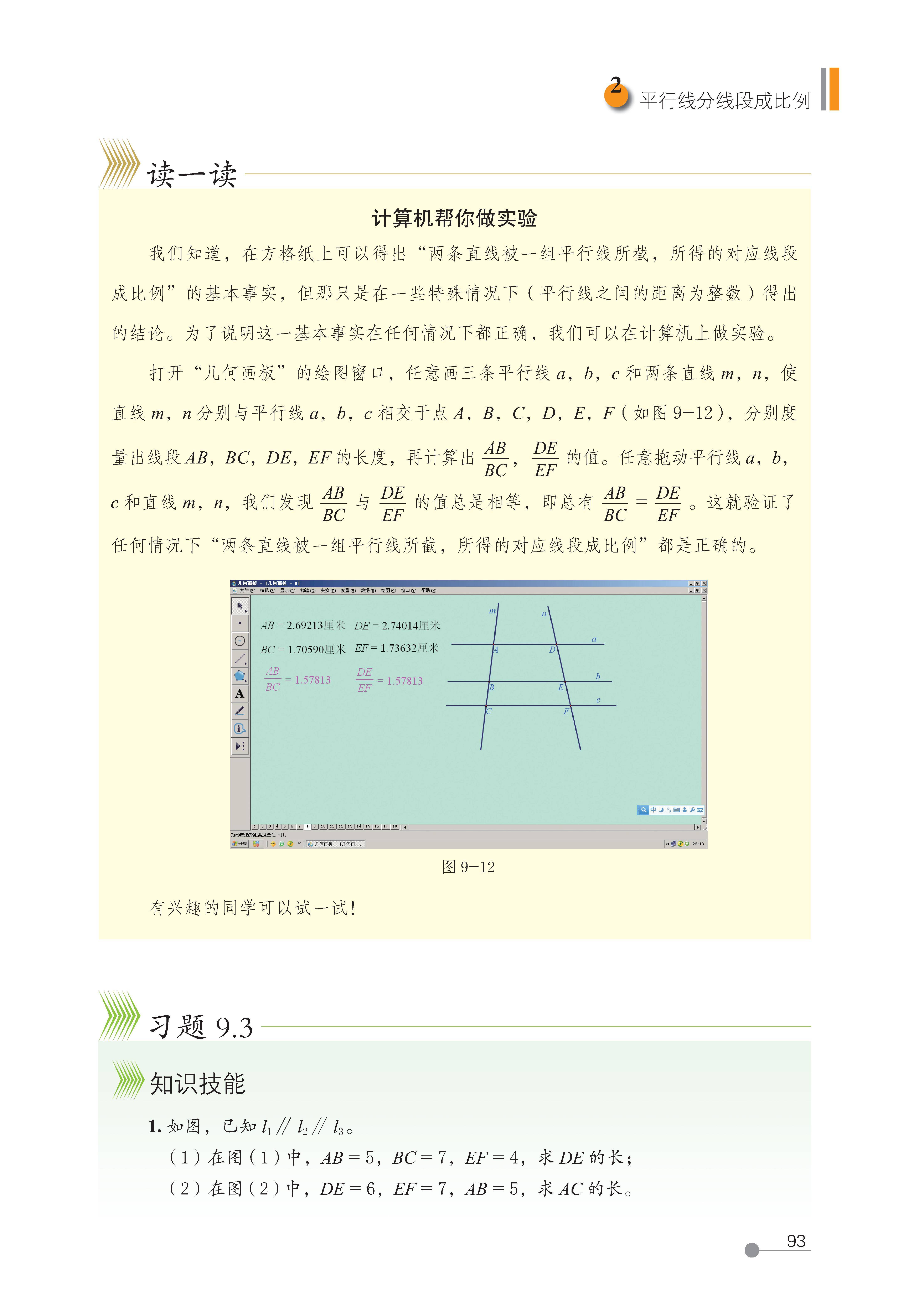
2 平行线分线段成比例

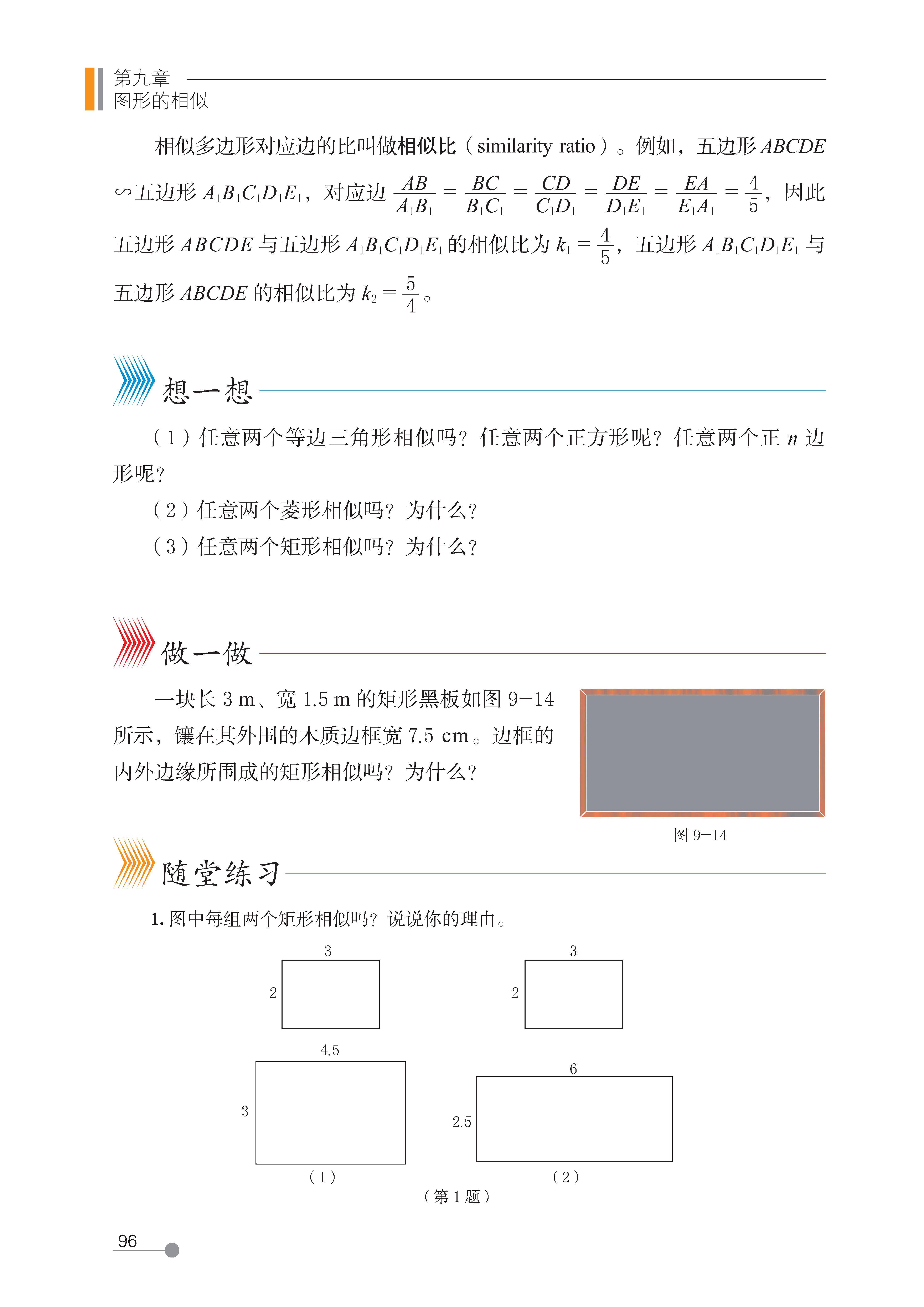
3 相似多边形

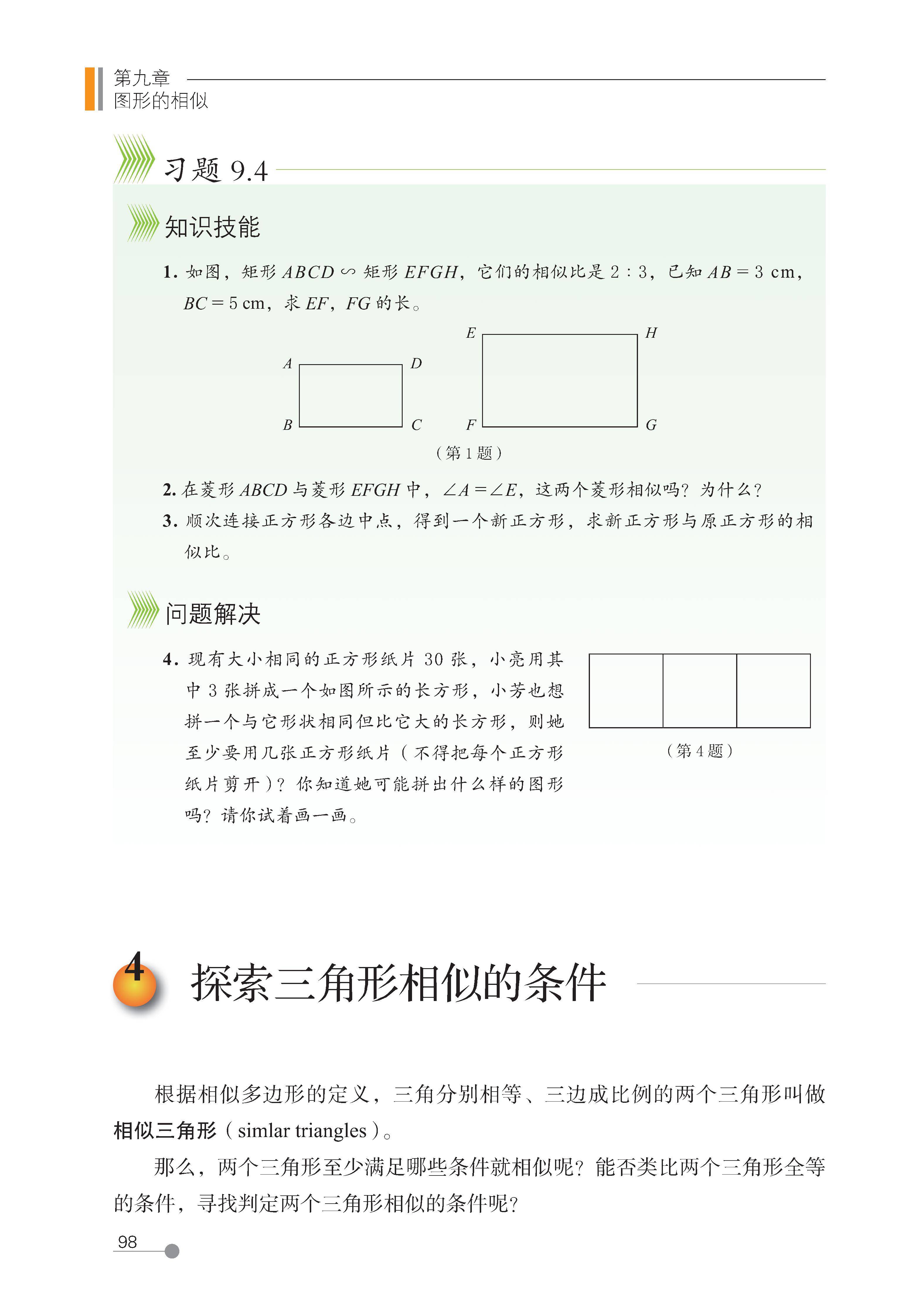
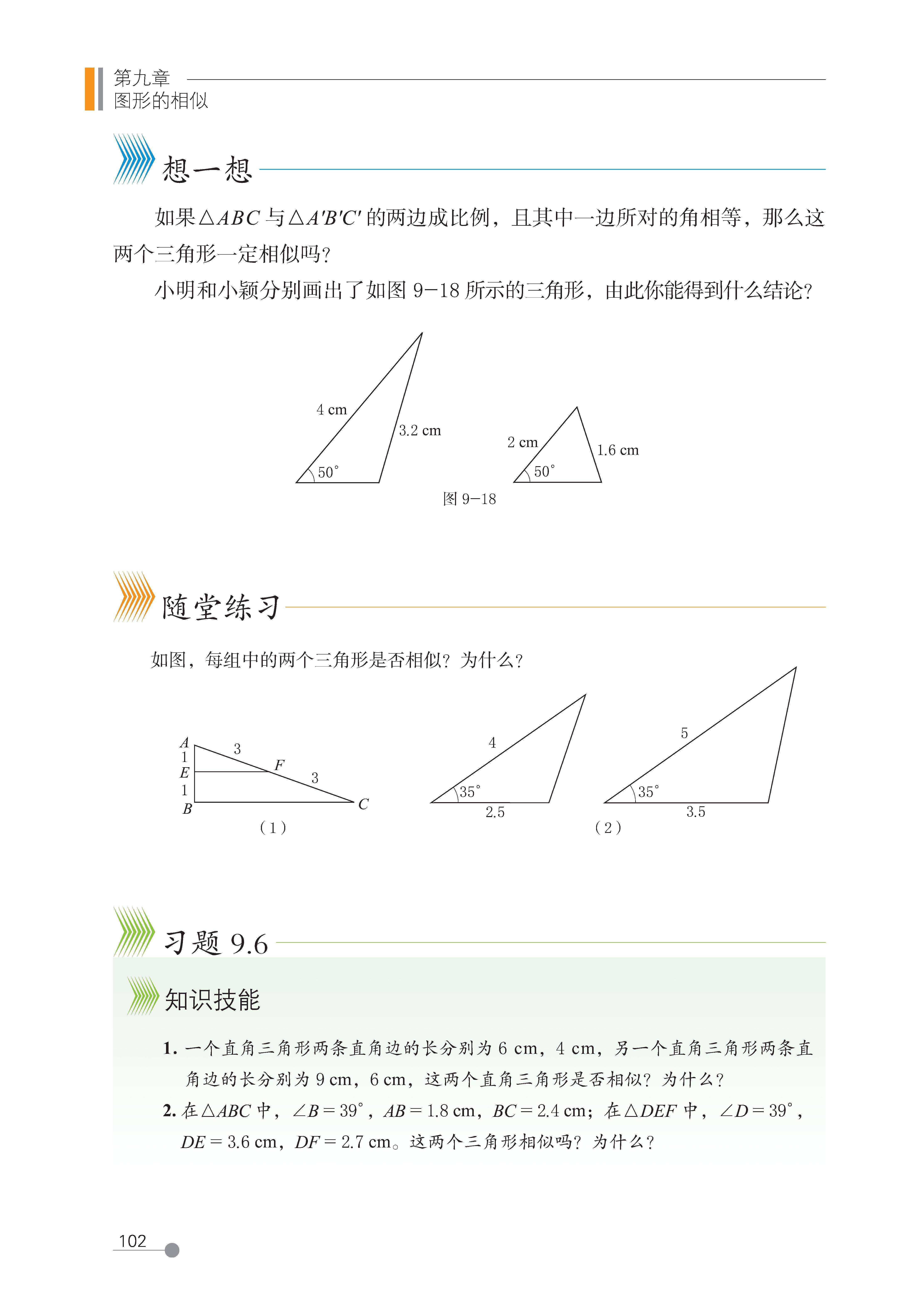
4 探索三角形相似的条件

5 相似三角形判定定理的证明

6 黄金分割

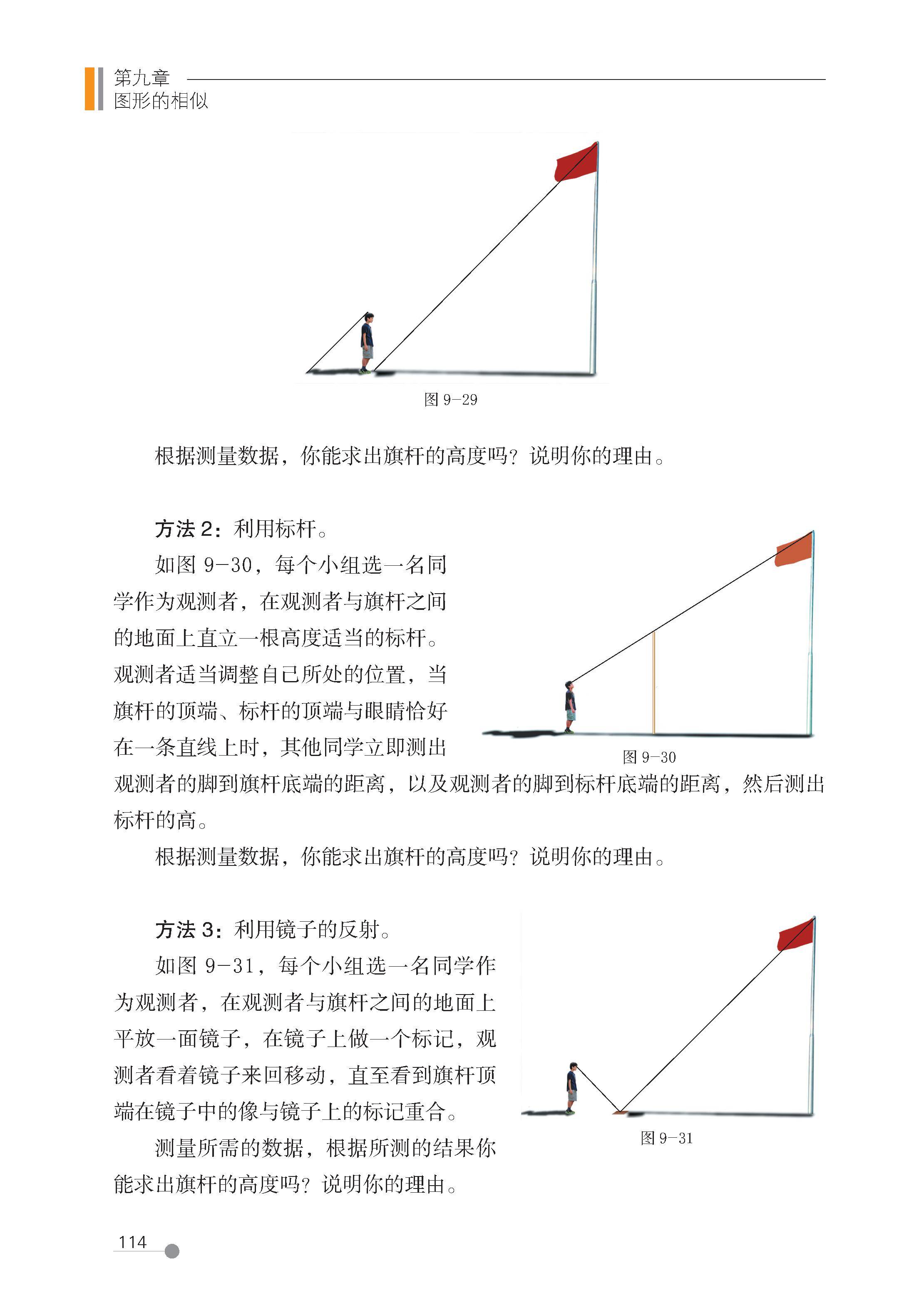
7 利用相似三角形测高

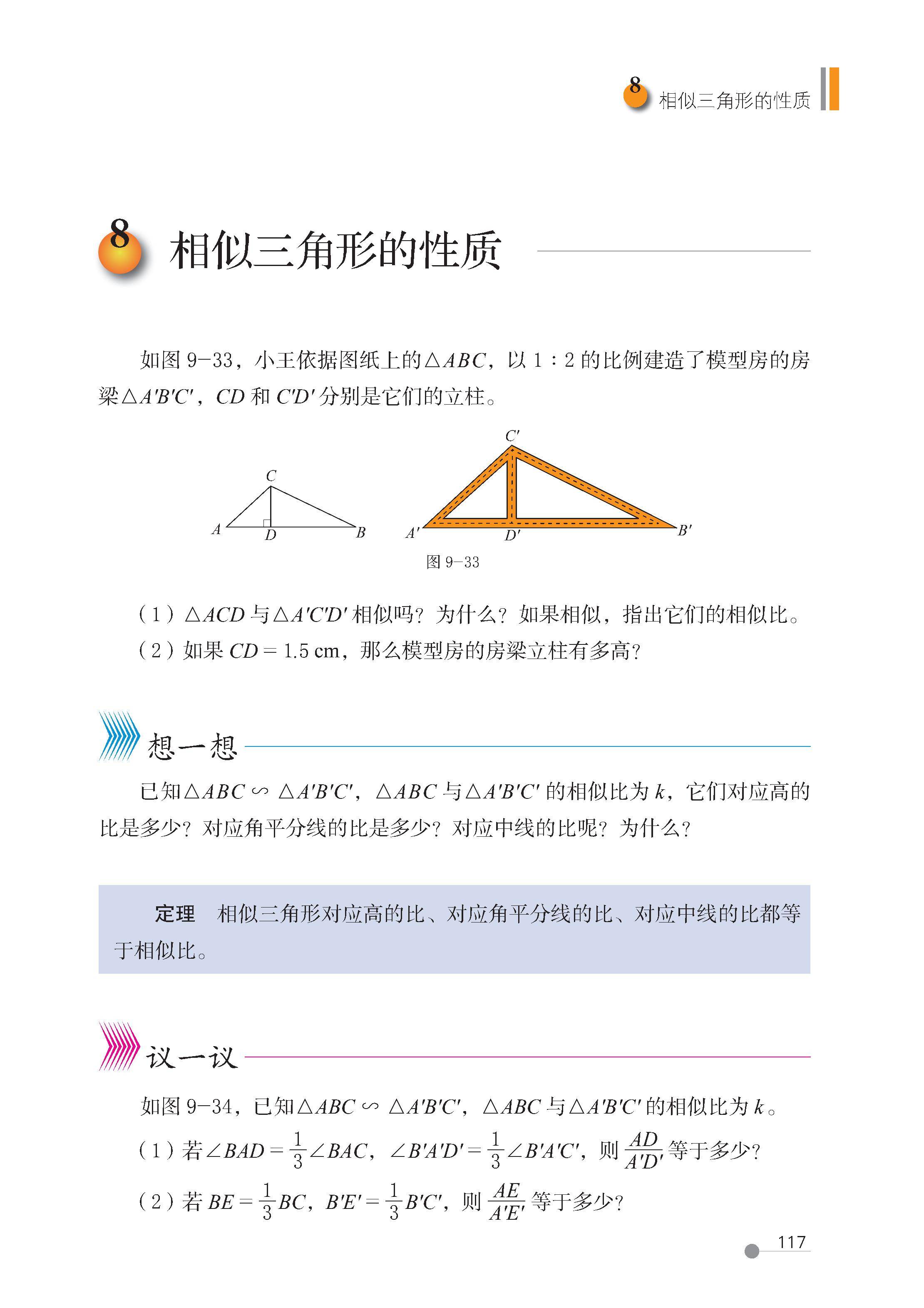
8 相似三角形的性质

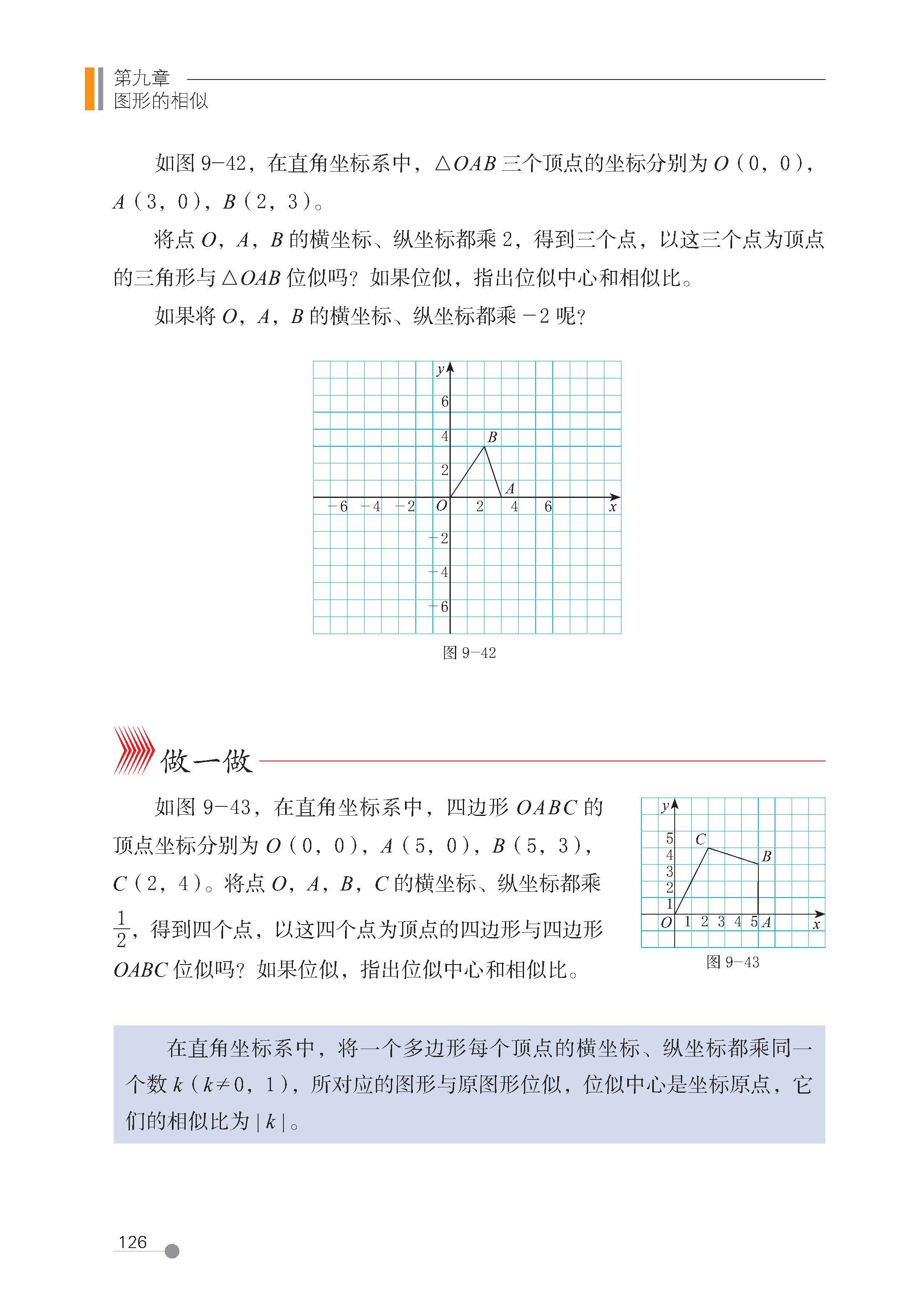
9 利用位似放缩图形

回顾与思考

复习题

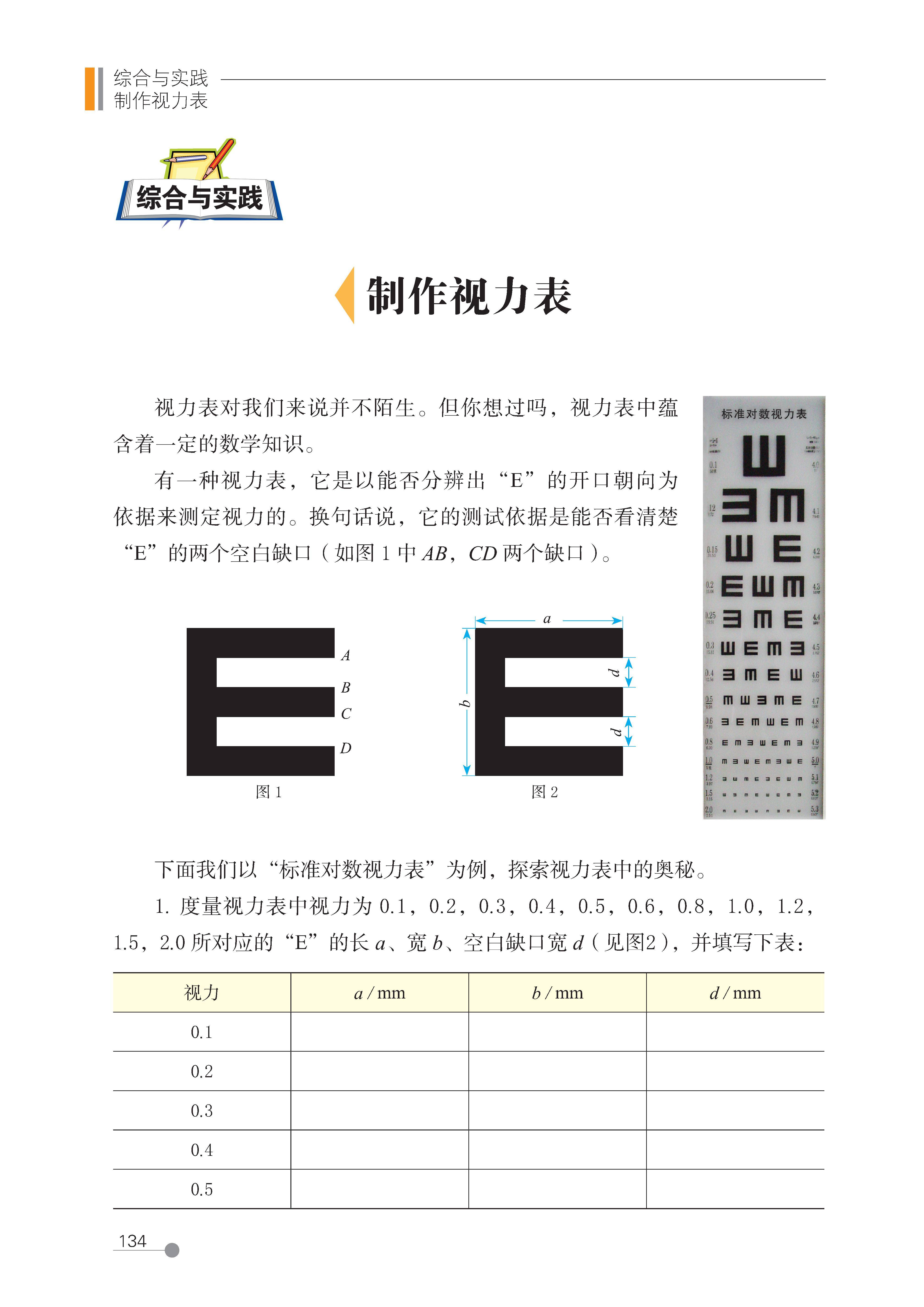
综合与实践 制作视力表

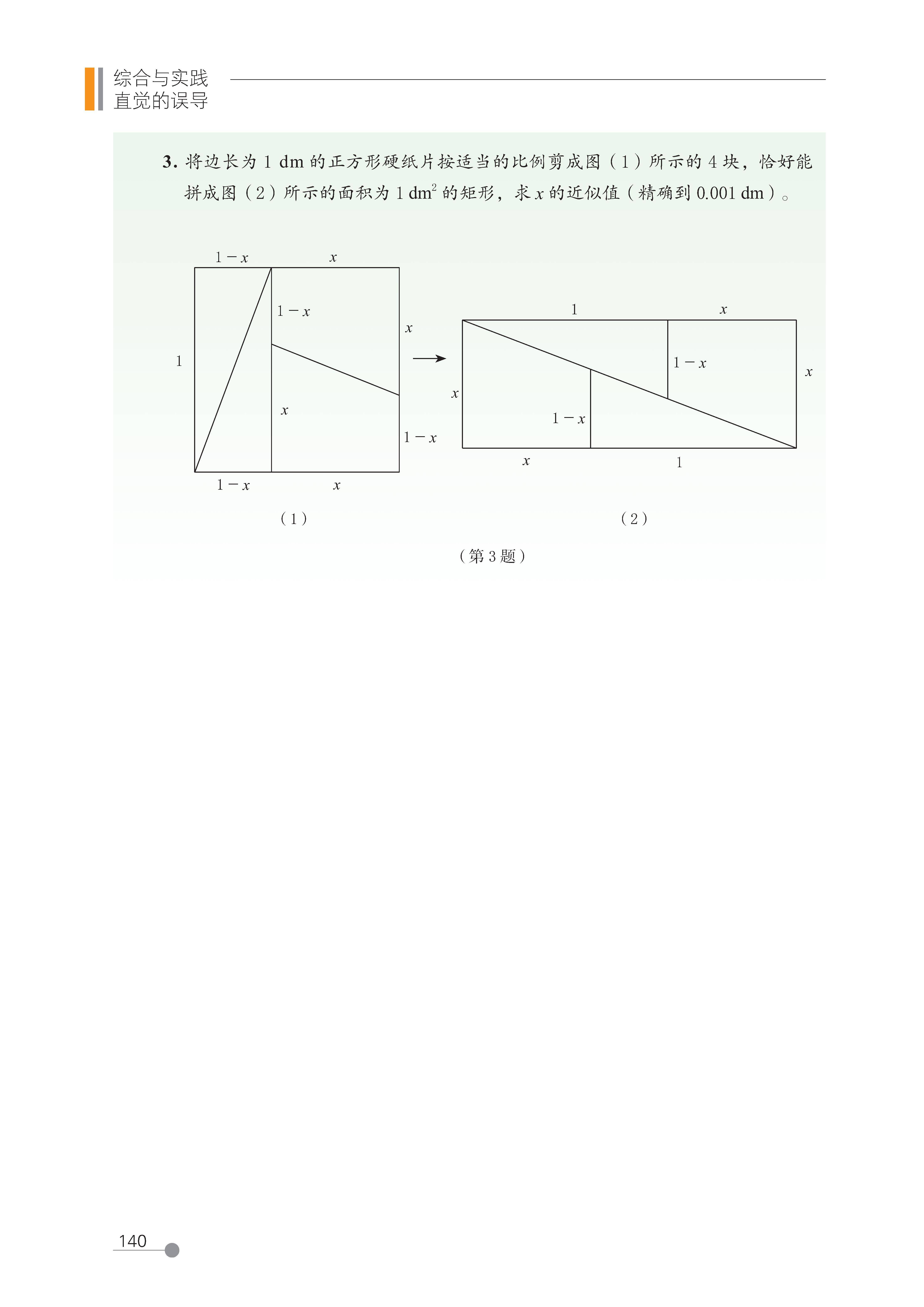
综合与实践 直觉的误导

总复习题

在鲁教版八年级下册数学的四章内容中，第九章 “图形的相似” 通常被认为是知识点最难的一章。这一结论基于知识点的抽象性、逻辑关联性、对综合能力的要求，以及学生的普遍学习反馈，具体可通过与其他章节的对比的和自身难点拆解来分析：

一、先明确各章难点的 “梯度”：从易到难排序

要判断 “最难”，需先梳理四章的核心难点及学习门槛：

章节 核心内容 主要难点 学习门槛

第六章 特殊平行四边形 菱形、矩形、正方形的性质与判定 1. 区分三种特殊图形的 “特殊条件”（如菱形需 “邻边相等”，矩形需 “直角”）；

2. 综合证明题中 “多性质联用”（如结合平行四边形性质 + 菱形对角线垂直） 低 - 中，基于上册 “平行四边形” 基础，逻辑链条较直接，定理多为 “平行四边形 + 1 个特殊条件”，易归纳

第七章 二次根式 概念、性质、运算（加减乘除、分母有理化） 1. 二次根式的非负性（√a 中 a≥0，√a≥0）的灵活应用；

2. 分母有理化的步骤（如含分母√a 或√a±√b 的变形） 中，知识点相对独立，运算有固定规则，虽需细心，但无复杂逻辑关联，练熟即可掌握

第八章 一元二次方程 解法（配方法、公式法、因式分解法）、根与系数的关系、应用 1. 配方法的步骤（二次项系数不为 1 时的变形）；

2. 判别式（Δ=b²-4ac）与根的情况的关联；

3. 实际应用中 “等量关系建立”（如增长率、面积问题） 中，解法有固定流程（如公式法直接代入），应用题型虽多，但 “套路性” 强，通过归类练习可突破

第九章 图形的相似 成比例线段、相似多边形、相似三角形（判定 + 性质）、位似 1. 比例式的变形（合比、等比性质的应用）；

2. 相似三角形的 “对应关系” 判断（复杂图形中找对应角 / 边）；

3. 辅助线构造相似（如作平行线）；

4. 相似性质与全等的混淆（如面积比 = 相似比 ²，而非相似比）；

5. 位似与坐标的结合（位似中心、位似比对坐标的影响） 高，知识点抽象且环环相扣，需同时具备 “代数变形能力”（比例式）和 “几何图形分析能力”（找相似），综合度极高

二、为什么 “图形的相似” 最难？核心难点拆解

“图形的相似” 的难度本质是 “抽象性 + 综合性”，具体体现在以下 4 个层面：

1. 概念抽象：从 “全等” 到 “相似”，认知跨度大

学生在七年级已学 “全等三角形”（形状相同、大小相等），而 “相似” 是 “形状相同、大小成比例”，是全等的 “一般情况”（全等是相似比为 1 的特殊相似）。这种 “从特殊到一般” 的抽象升级，容易让学生陷入误区：

混淆 “全等判定” 与 “相似判定”：比如误将 “SSA” 用于相似判定（实际相似判定为 AA、SAS、SSS，无 SSA，但全等中 SSA 不成立）；

忽略 “比例关系”：全等只需 “对应边相等”，而相似需 “对应边成比例”，学生常忘记 “比例” 这一核心条件（如误判 “两边对应相等” 的三角形相似）。

2. 比例式变形：代数能力与几何结合的 “第一道坎”

“相似” 的基础是 “成比例线段”，而比例式的变形（如交叉相乘、合比性质

a

=

d

c

⇒

a±b

=

d

c±d

、等比性质

a

=

d

c

=⋯=

n

m

⇒

b+d+⋯+n

a+c+⋯+m

=

a

）需要极强的代数变形能力，且需结合几何图形应用：

例：若 DE∥BC（△ABC 中），则

AB

AD

=

AC

AE

=

BC

DE

，学生需灵活将 “线段比” 转化为 “已知边长求未知边长”，若比例式写错或变形出错，后续全错；

难点：比例式的 “对应性”（如 AD 对应 AB，而非 AD 对应 AC），一旦对应关系错，比例式完全失效。

3. 相似三角形的判定与性质：“找图” 比 “记定理” 更难

判定难点：相似三角形的判定定理（AA、SAS、SSS）本身不难记，但难点在于 “在复杂图形中找到相似三角形”—— 比如含 “一线三垂直”“A 型”“X 型” 模型的图形，或需要添加辅助线（如作平行线、连接线段）构造相似的题目，对 “图形拆解能力” 要求极高。

例：在梯形 ABCD 中，AB∥CD，若要证△AOB∽△COD，需先识别 “对顶角相等”+“平行线的内错角相等”（AA 判定），若学生看不出 “X 型” 模型，就无法入手。

性质难点：相似三角形的性质（对应角相等、对应边成比例、周长比 = 相似比、面积比 = 相似比 ²、对应高 / 中线 / 角平分线比 = 相似比）易混淆，尤其是 “面积比与相似比的平方关系”—— 学生常误记为 “面积比 = 相似比”，导致计算错误。

4. 位似图形：几何与代数的 “综合暴击”

位似是 “相似的特殊情况”（需满足 “对应顶点连线交于一点”“对应边平行或共线”），且常与平面直角坐标系结合，要求学生同时处理：

位似中心的确定（可能在图形内、图形外、坐标轴上）；

位似比的计算（需判断是 “放大” 还是 “缩小”，比的顺序是否正确）；

位似图形的坐标变化（如以原点为位似中心，相似比为 k，则点 (x,y) 变为 (kx,ky) 或 (-kx,-ky)）。

这种 “几何图形特征 + 坐标代数计算” 的综合题，是学生的高频丢分点，也是本章难度的 “顶峰”。

三、为什么其他章节相对容易？

第六章 “特殊平行四边形”：所有性质和判定都基于 “平行四边形”，只需额外记住 “1 个特殊条件”（如菱形 = 平行四边形 + 邻边相等，矩形 = 平行四边形 + 直角），逻辑上是 “递进式” 而非 “跨越式”，证明题的辅助线也较少；

第七章 “二次根式”：核心是 “运算规则”，如√a・√b=√(ab)（a≥0,b≥0）、√a/√b=√(a/b)（a≥0,b>0），虽有 “分母有理化” 等细节，但只要掌握步骤，无需复杂的图形分析或逻辑推理；

第八章 “一元二次方程”：解法有固定流程（如配方法：移项→化二次项系数为 1→配方→开方→求解），根与系数的关系（韦达定理）虽需理解，但应用题型多为 “已知根求系数”“已知系数求根的关系”，套路性强，练习后易掌握。

四、学习 “图形的相似” 的建议（针对性突破难点）

先抓 “基础关联”：复习 “全等三角形”，明确 “相似是全等的一般情况”，对比两者的判定定理（如全等的 ASA 对应相似的 AA，全等的 SSS 对应相似的 SSS），避免混淆；

强化 “比例式变形”：单独练习比例式的交叉相乘、合比、等比性质，确保代数变形不出错；

总结 “相似模型”：归纳常见的相似图形模型（A 型、X 型、一线三垂直、母子相似），熟悉每种模型的 “对应角 / 边” 特征，遇到复杂图形时先 “拆模型”；

重视 “辅助线”：重点掌握 “作平行线构造相似” 的辅助线方法（如在三角形中过一点作某边的平行线，构造 “A 型” 相似）；

区分 “性质细节”：用表格对比 “相似三角形的性质”（如相似比 k 与周长比、面积比的关系），避免记混。

综上，从知识点的抽象性、综合能力要求、学生学习反馈来看，第九章 “图形的相似” 是鲁教版八年级下册数学中最难的一章。