如需全套各科电子课本PDF版（可下载打印）

请关注公众号“禾沐教辅网”（ ID: hemujiaofu ）

关注后自动获取资料合集（包含下列推荐资料）

500T学习资料分享

同步25年秋季学校教学进度持续更新.......

鲁教版七年级上册数学电子课本的目录如下：

第一章 三角形

第 1 节 认识三角形

第 2 节 图形的全等

全等三角形

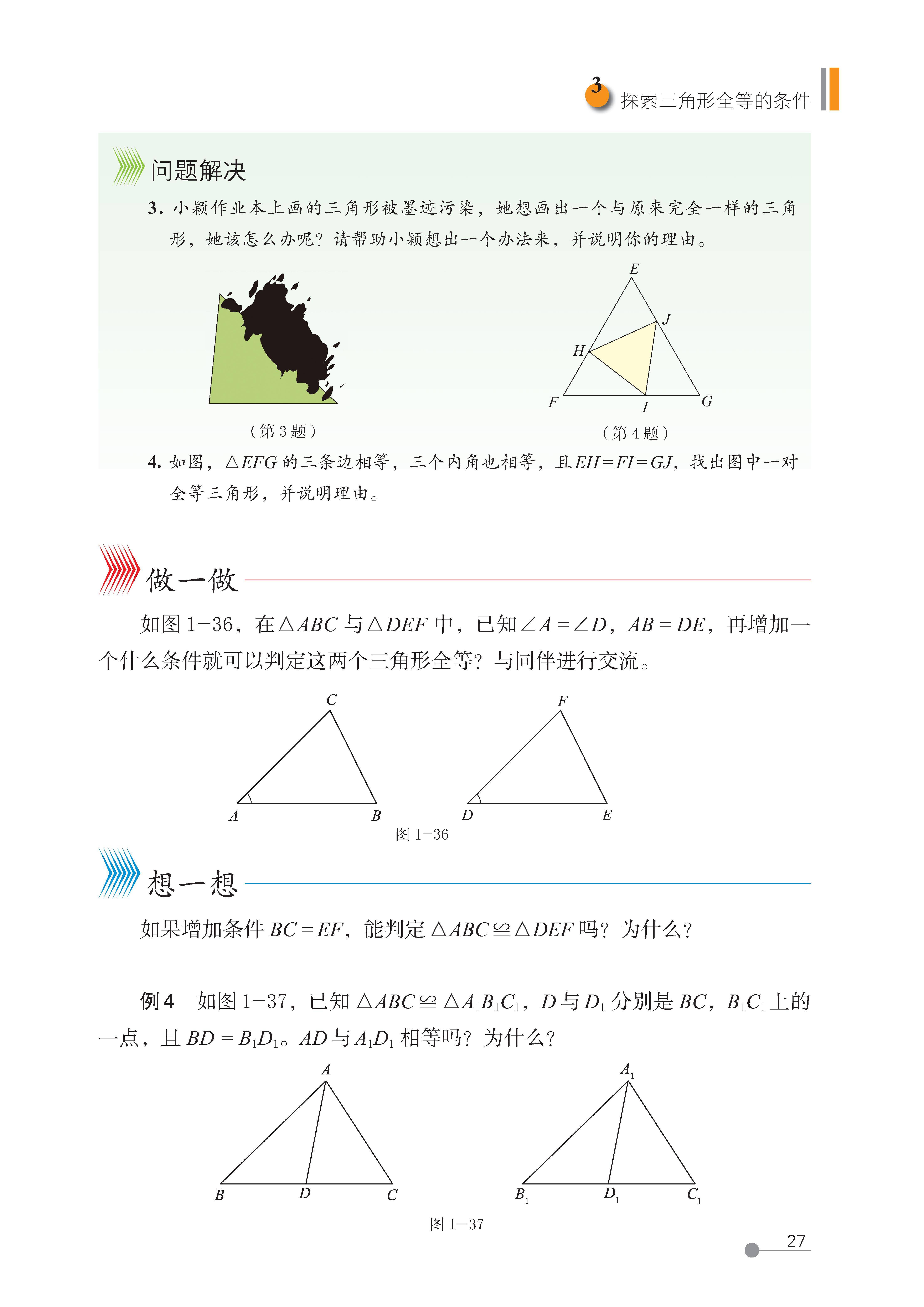
第 3 节 探索三角形全等的条件

边边边（SSS）

角边角（ASA）角角边（AAS）

边角边（SAS）

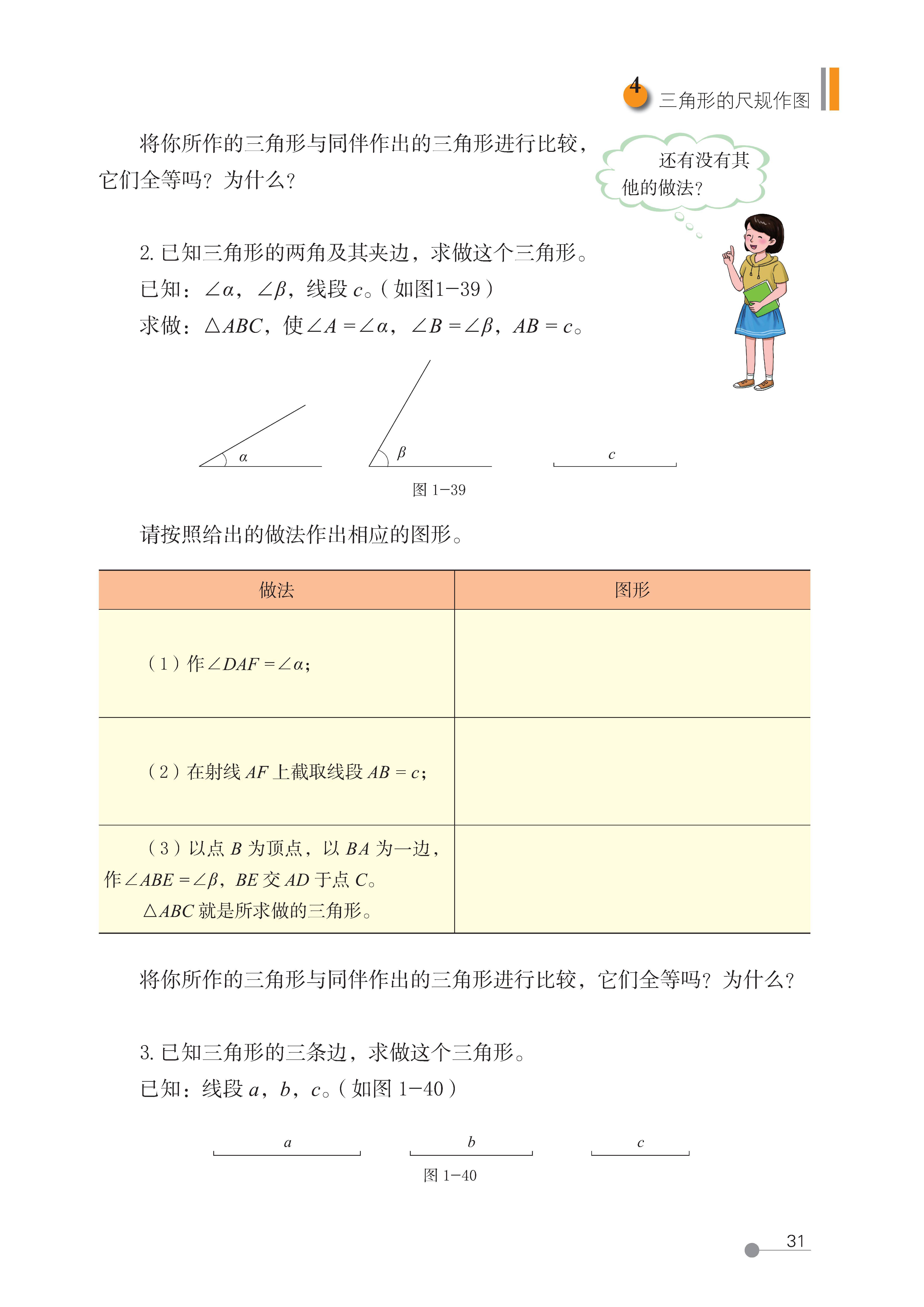
第 4 节 三角形的尺规作图

第 5 节 利用三角形全等测距离

第二章 轴对称

第 1 节 轴对称现象

第 2 节 探索轴对称的性质

第 3 节 简单的轴对称图形

第 4 节 利用轴对称进行设计

第三章 勾股定理

第 1 节 探索勾股定理

第 2 节 一定是直角三角形吗

第 3 节 勾股定理的应用举例

第四章 实数

第 1 节 无理数

第 2 节 平方根（二次方根）

第 3 节 立方根（三次方根）

第 4 节 估算

第 5 节 用计算器开方

第 6 节 实数（有理数和无理数）

计算器运用于功能探索

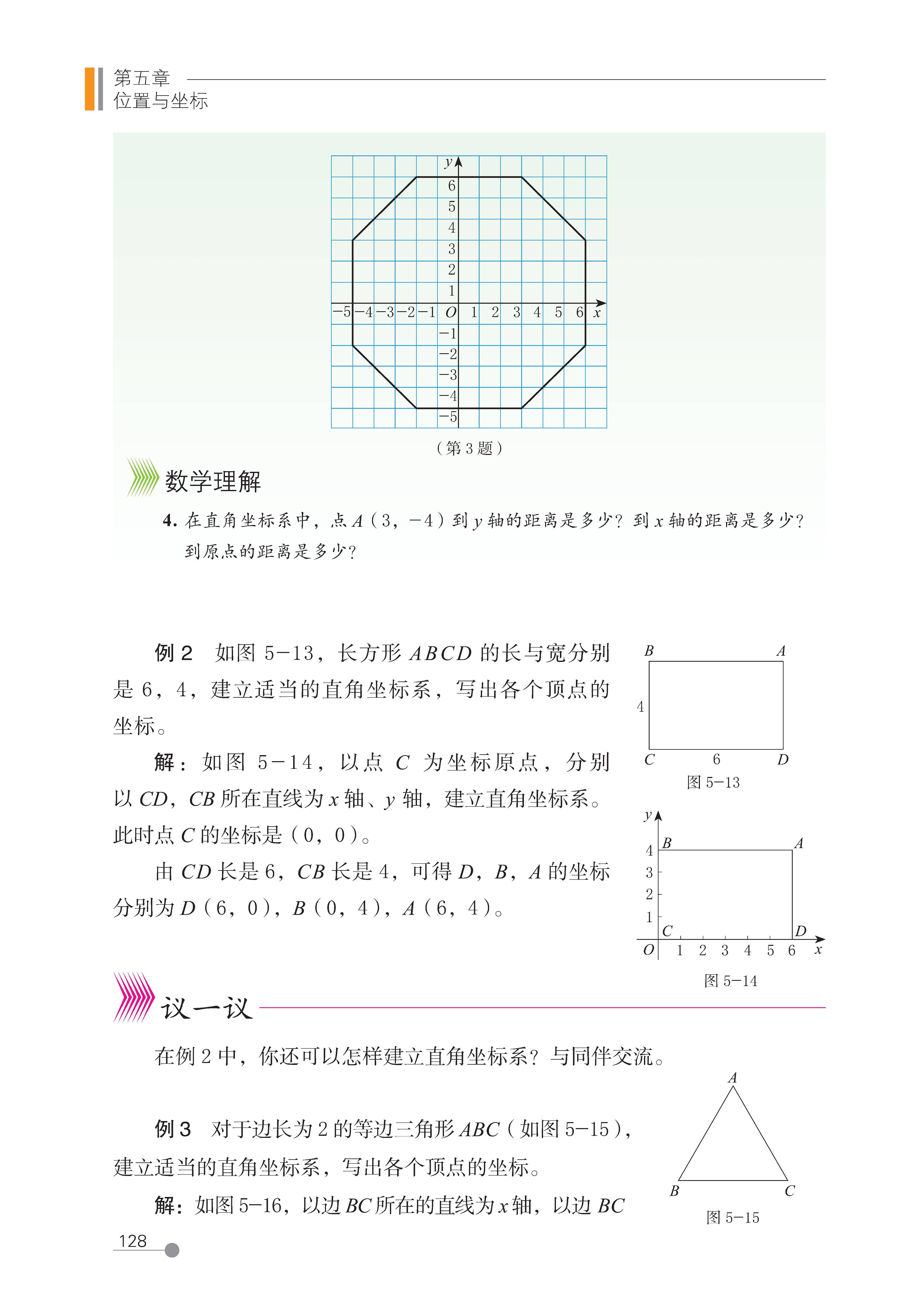
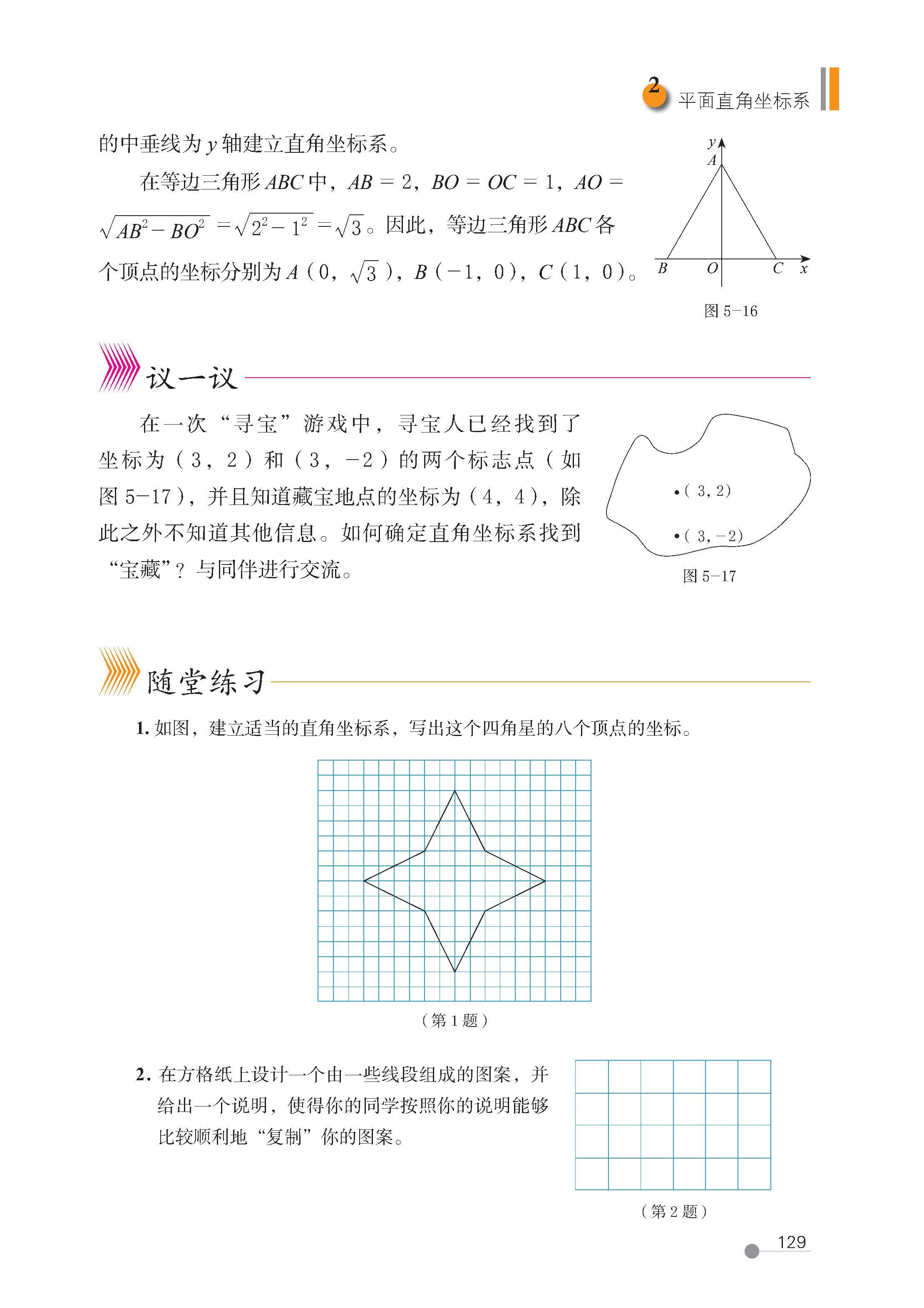
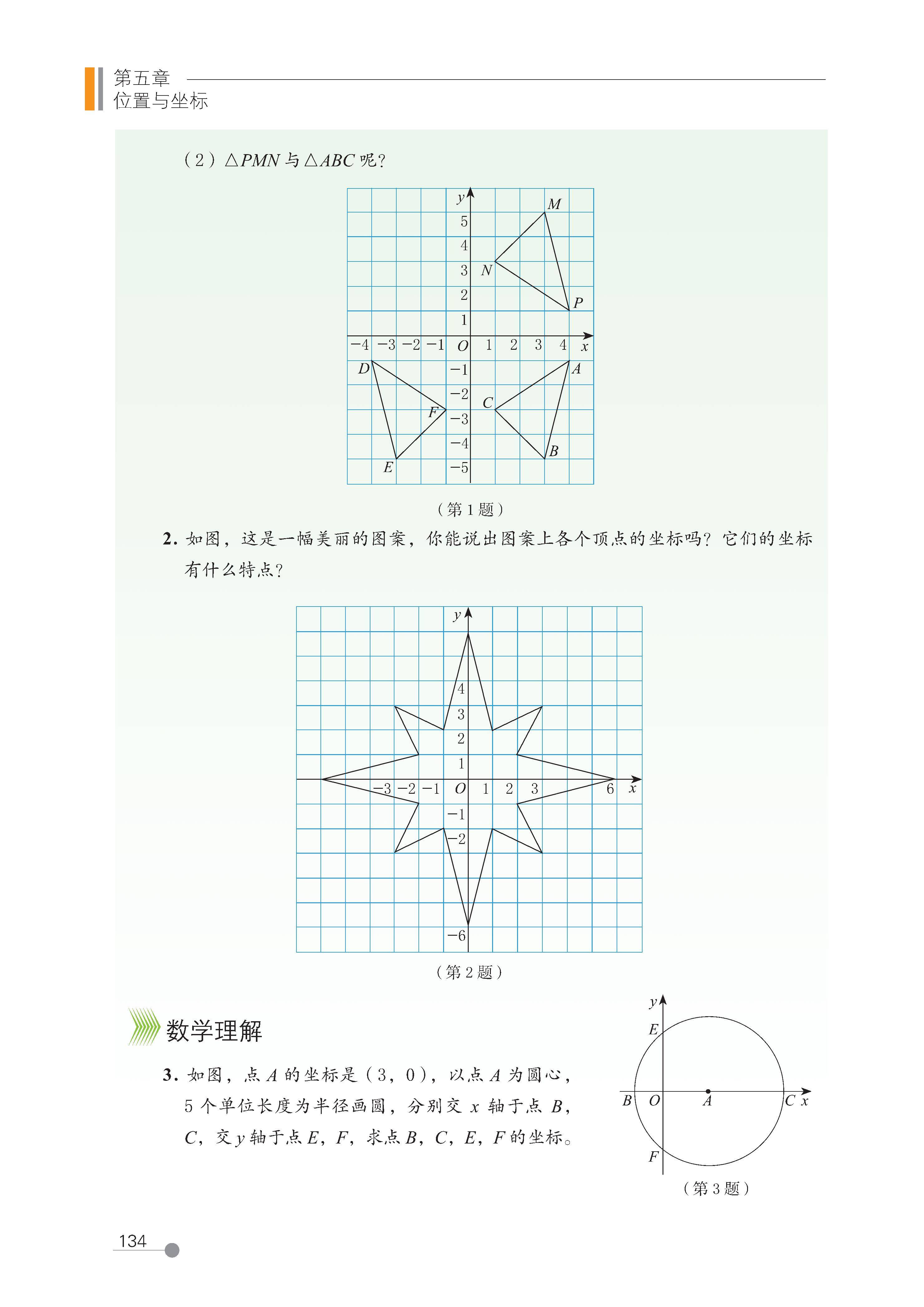
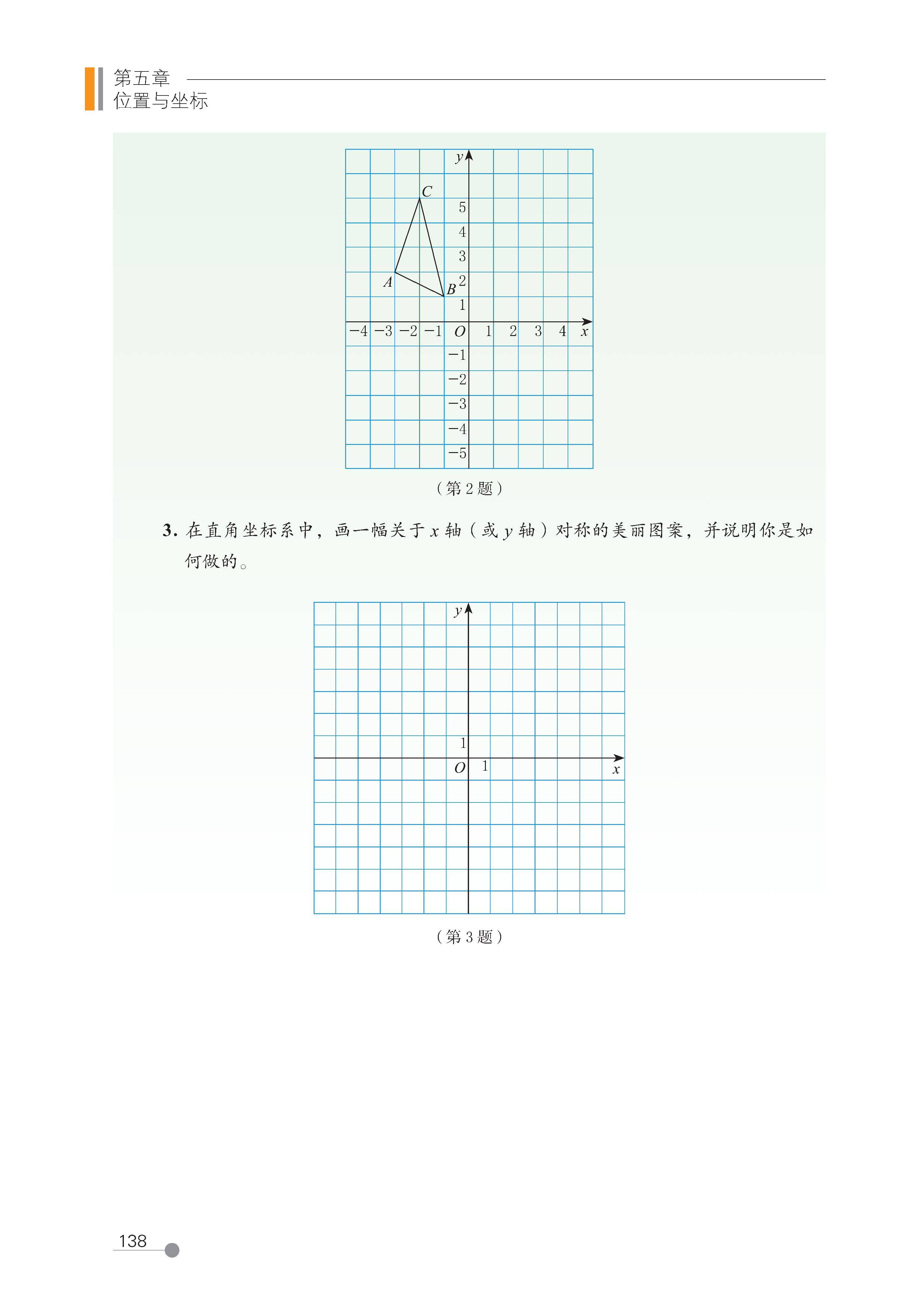
第五章 位置与坐标

第 1 节 确定位置

第 2 节 平面直角坐标系

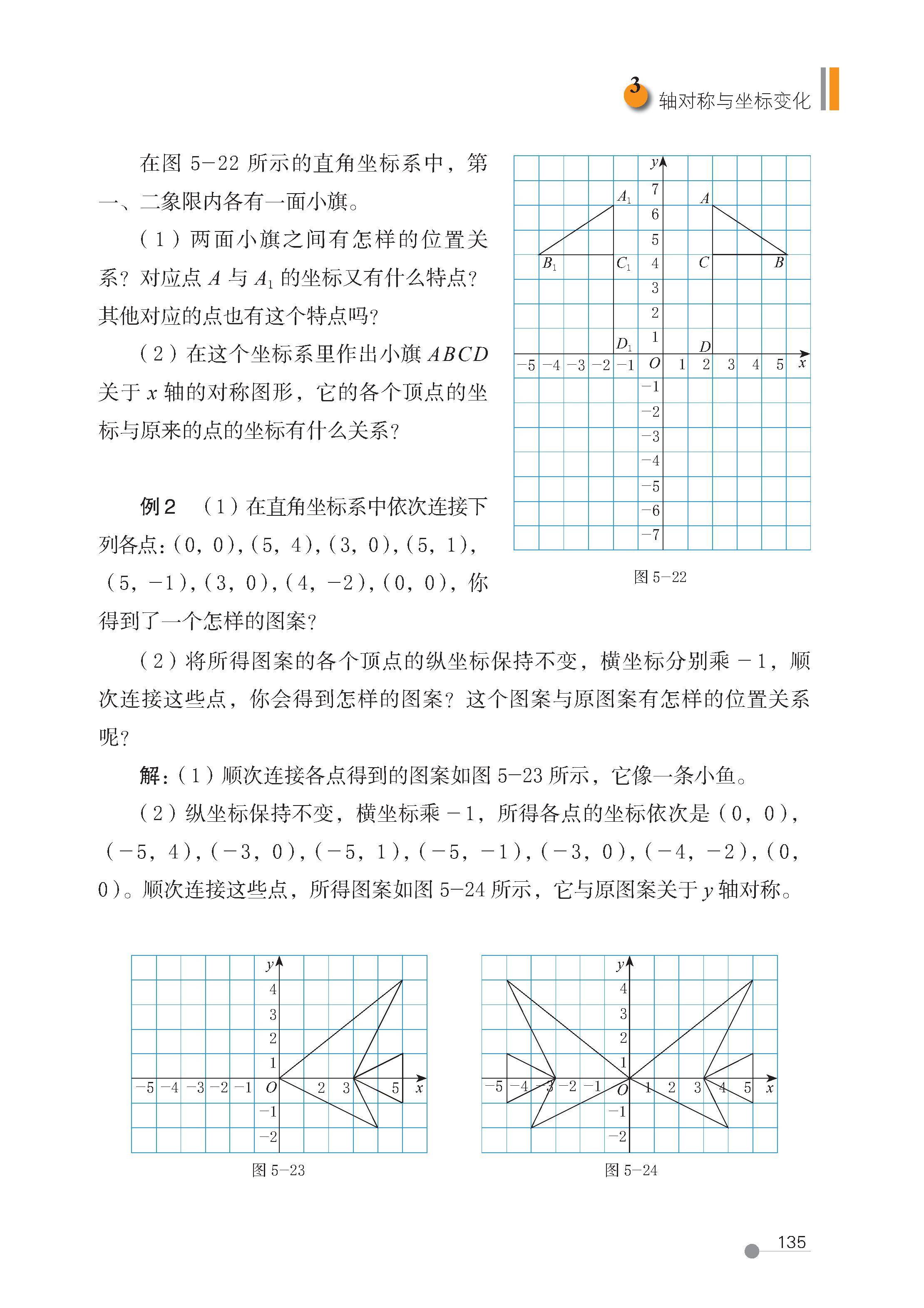
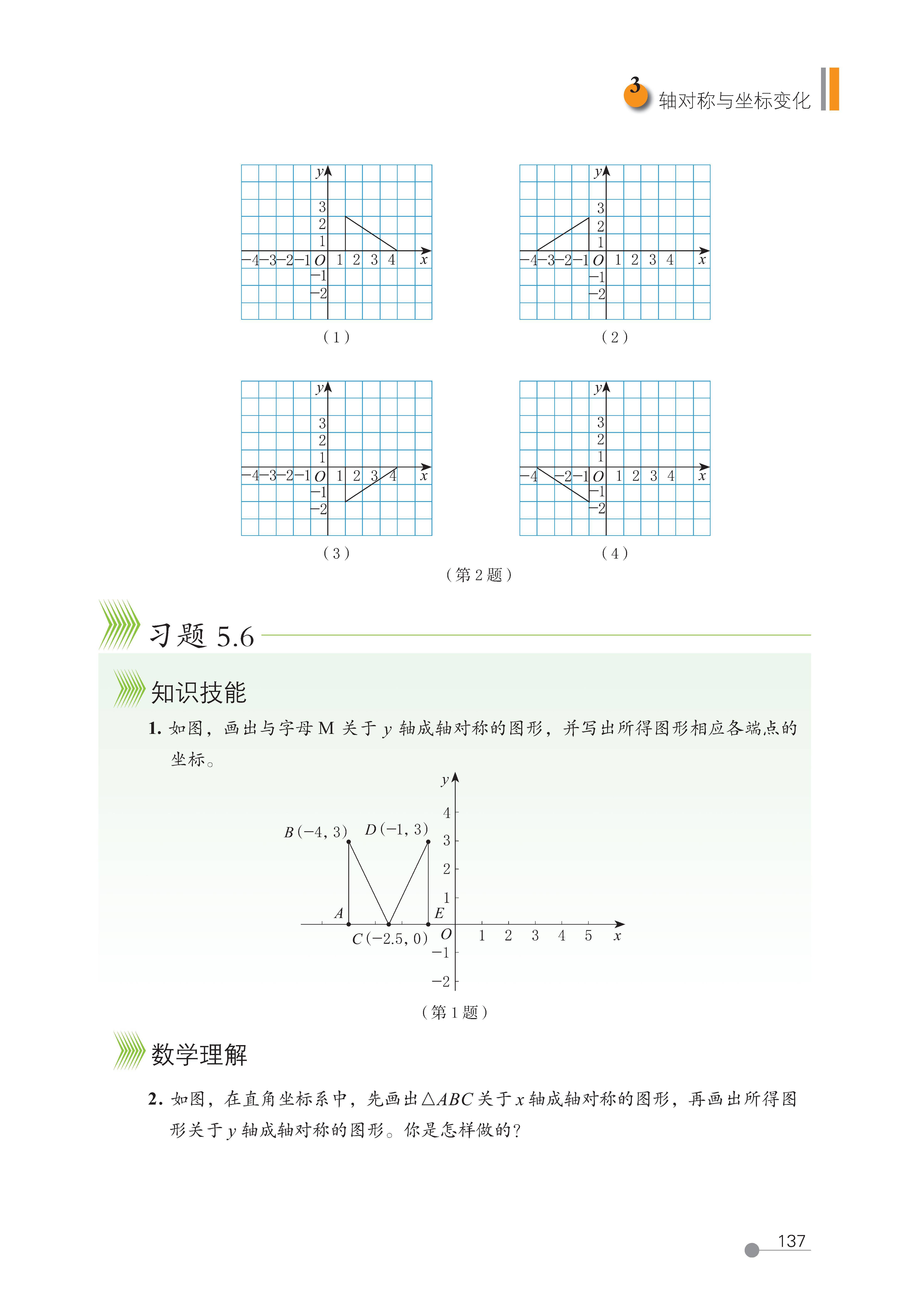
第 3 节 轴对称与坐标变化

第六章 一次函数

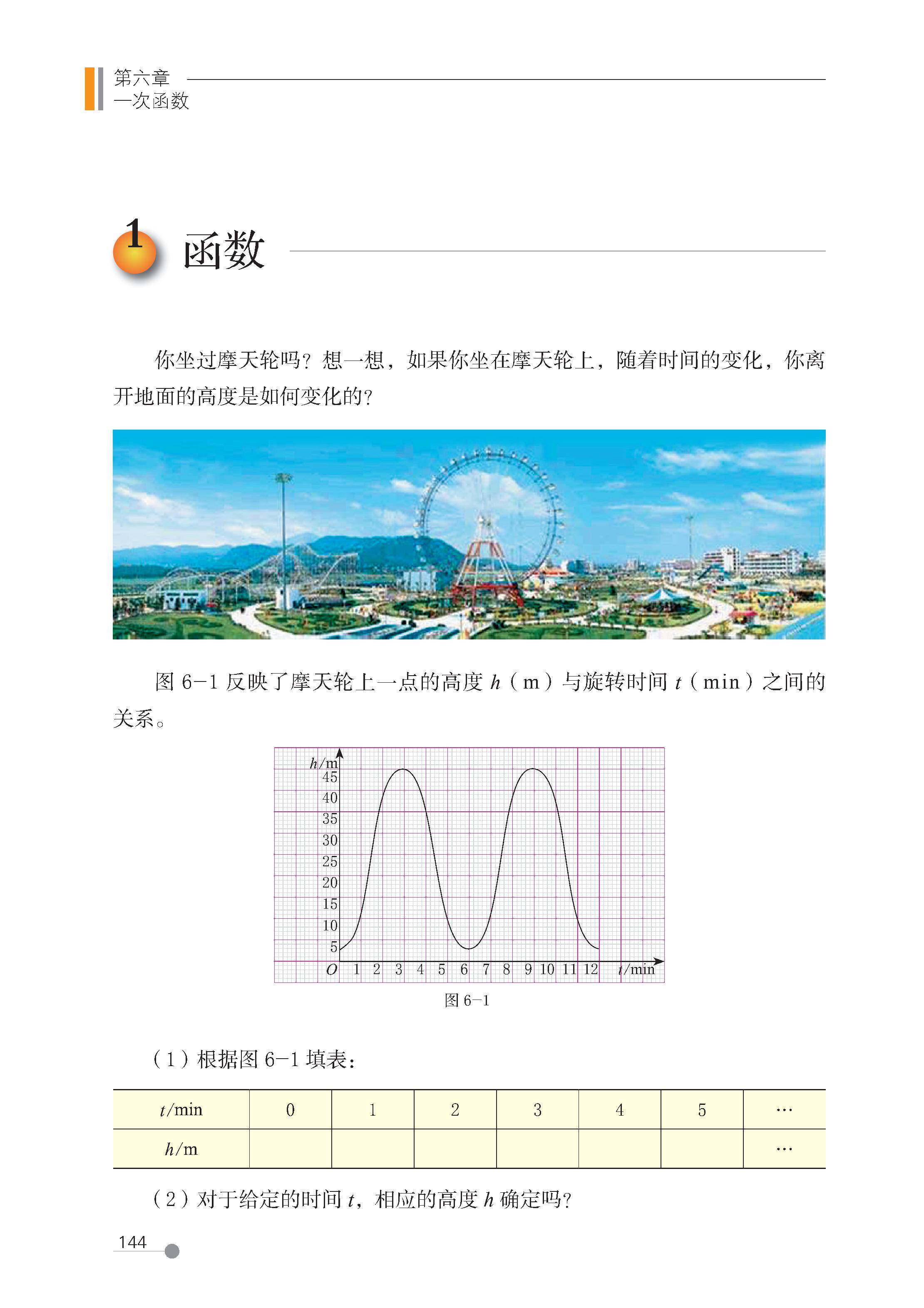
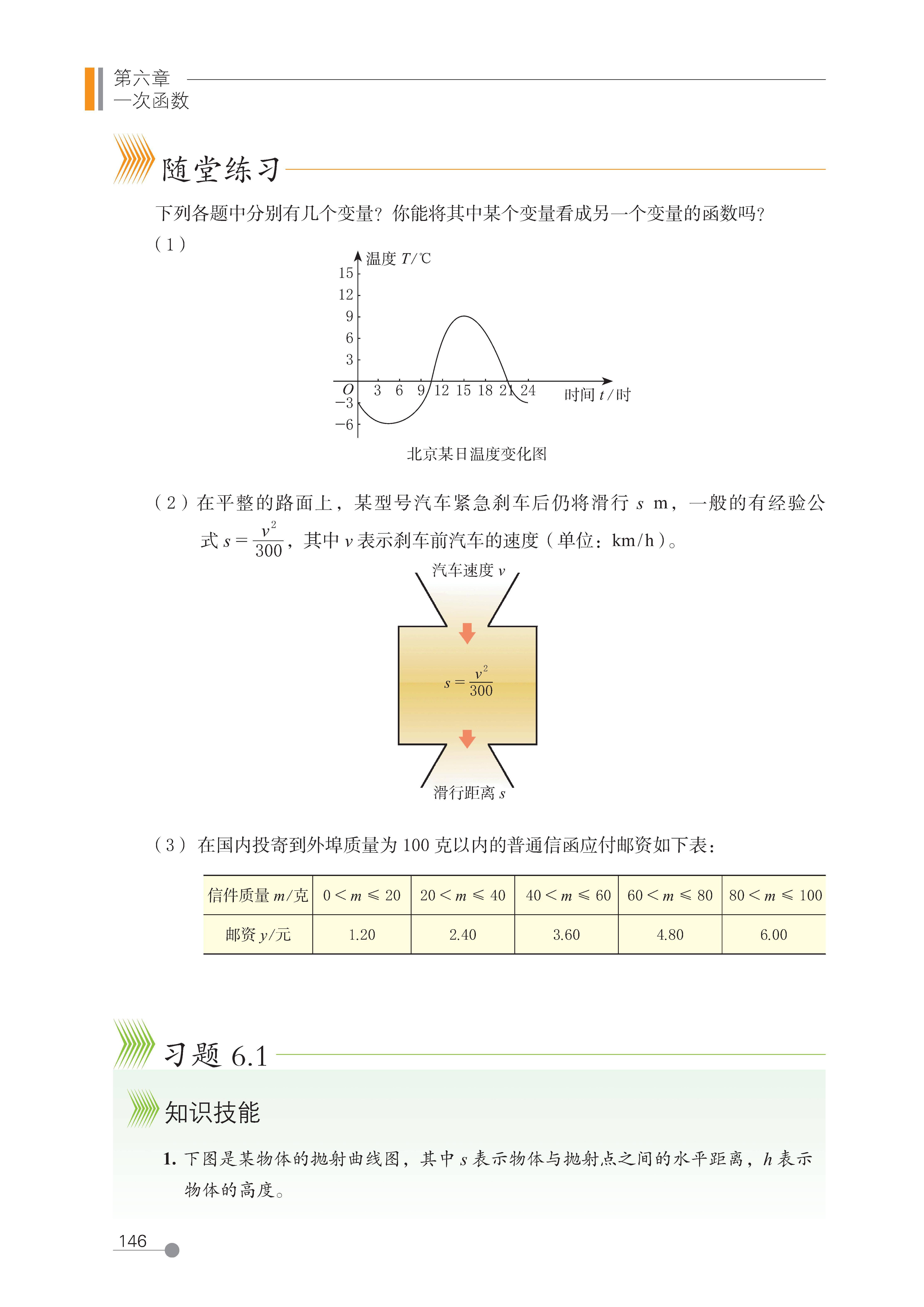
第 1 节 函数（正比例函数）

第 2 节 一次函数

第 3 节 一次函数的图象 y=kx+b

第 4 节 确定一次函数的表达式

第 5 节 一次函数的应用

总复习

鲁教版七年级上册数学第一章 “三角形” 是初中几何的核心基础章节，围绕三角形的概念、性质、全等判定及应用展开，以下是该章节的重要知识点梳理，按课本小节逻辑划分，覆盖核心概念、性质、定理及应用：

一、第 1 节：认识三角形

1. 三角形的基本定义与表示

定义：由不在同一条直线上的三条线段首尾顺次相接所组成的封闭图形叫做三角形。

表示方法：用符号 “△” 表示，如顶点为 A、B、C 的三角形，记作 “△ABC”，读作 “三角形 ABC”。

构成要素：

3 个顶点（A、B、C）、3 条边（AB、BC、AC，可表示为 a、b、c，对应顶点对边）、3 个内角（∠A、∠B、∠C）。

2. 三角形的分类（按边 / 按角）

分类标准 具体类型 定义 / 特征

按边分类 不等边三角形 三条边都不相等的三角形

等腰三角形 有两条边相等的三角形（相等的边叫 “腰”，第三边叫 “底边”；两腰的夹角叫 “顶角”，腰与底边的夹角叫 “底角”）

等边三角形（正三角形） 三条边都相等的三角形（特殊的等腰三角形，三个角均为 60°）

按角分类 锐角三角形 三个内角都是锐角（小于 90°）的三角形

直角三角形 有一个内角是直角（等于 90°）的三角形（直角所对的边叫 “斜边”，另两条边叫 “直角边”）

钝角三角形 有一个内角是钝角（大于 90° 且小于 180°）的三角形

3. 三角形的核心性质

性质 1：内角和定理：三角形的三个内角和等于 180°（可通过 “剪拼内角” 或 “作平行线” 证明）。

推论：直角三角形的两个锐角互余（和为 90°）；三角形的一个外角等于与它不相邻的两个内角的和。

性质 2：三边关系：三角形任意两边之和大于第三边；任意两边之差小于第三边（判断三条线段能否构成三角形的依据）。

例：若三角形三边为 a、b、c（a≤b≤c），则需满足 a + b > c。

性质 3：重要线段（高频考点）：

线段类型 定义 性质

高线（高） 从三角形的一个顶点向它的对边所在直线作垂线，顶点与垂足之间的线段 ① 锐角三角形三条高在内部；直角三角形两条高与直角边重合，一条在内部；钝角三角形两条高在外部，一条在内部；② 三角形三条高交于一点（垂心）

中线 连接三角形一个顶点与对边中点的线段 ① 平分对边（将对边分成两段相等的线段）；② 三角形三条中线交于一点（重心，重心到顶点的距离是到对边中点距离的 2 倍）；③ 中线将三角形分成面积相等的两个小三角形

角平分线 三角形一个内角的平分线与对边相交，顶点与交点之间的线段 ① 平分内角（将内角分成两个相等的角）；② 三角形三条角平分线交于一点（内心，内心到三边的距离相等）

二、第 2 节：图形的全等与全等三角形

1. 全等图形的定义与特征

定义：能够完全重合的两个图形叫做全等图形（形状相同、大小相等）。

特征：全等图形的对应边相等、对应角相等（后续全等三角形性质的基础）。

2. 全等三角形的定义与表示

定义：能够完全重合的两个三角形叫做全等三角形（重合的顶点叫 “对应顶点”，重合的边叫 “对应边”，重合的角叫 “对应角”）。

表示方法：用符号 “≌” 表示，如△ABC 与△DEF 全等，记作 “△ABC ≌ △DEF”（注意：对应顶点需写在对应位置，如 A 对应 D、B 对应 E、C 对应 F）。

3. 全等三角形的性质（核心考点）

全等三角形的对应边相等（如△ABC ≌ △DEF，则 AB=DE、BC=EF、AC=DF）；

全等三角形的对应角相等（如△ABC ≌ △DEF，则∠A=∠D、∠B=∠E、∠C=∠F）；

延伸性质：全等三角形的对应高线、对应中线、对应角平分线也相等；全等三角形的面积、周长相等。

三、第 3 节：探索三角形全等的条件（重中之重）

该部分是全章核心，需熟练掌握4 种判定定理，明确 “满足哪些条件可证明两个三角形全等”，同时注意 “易错的假判定”（如 SSA、AAA 不可用）。

1. 判定定理 1：边边边（SSS）

内容：三边分别相等的两个三角形全等（简记 “SSS”）。

应用场景：已知两个三角形的三条边对应相等（如 “用三根固定长度的木条钉三角形，形状大小唯一”，体现三角形的稳定性）。

示例：若 AB=DE、BC=EF、AC=DF，则△ABC ≌ △DEF（SSS）。

2. 判定定理 2：角边角（ASA）与角角边（AAS）

ASA（角边角）：

内容：两角及其夹边分别相等的两个三角形全等（简记 “ASA”）。

关键：“夹边” 是两个角的公共边（如∠A=∠D、AB=DE、∠B=∠E，AB 是∠A 与∠B 的夹边，DE 是∠D 与∠E 的夹边）。

AAS（角角边）：

内容：两角分别相等且其中一组等角的对边相等的两个三角形全等（简记 “AAS”）。

关系：ASA 和 AAS 可结合 “三角形内角和 180°” 互推，本质都是 “两角一边” 对应相等（注意区分 “夹边” 与 “对边”）。

示例：① 若∠A=∠D、AB=DE、∠B=∠E，则△ABC ≌ △DEF（ASA）；② 若∠A=∠D、∠B=∠E、BC=EF，则△ABC ≌ △DEF（AAS）。

3. 判定定理 3：边角边（SAS）

内容：两边及其夹角分别相等的两个三角形全等（简记 “SAS”）。

关键：“夹角” 是两条边的公共角（必须是夹角，非夹角不可，即 SSA 不能判定全等）。

易错点：若两边及其中一边的对角相等（SSA），则两个三角形不一定全等（可通过画图举例：固定 AB、AC 长度，∠B 为 AB 的对角，可画出两个不同的三角形）。

示例：若 AB=DE、∠A=∠D、AC=DF（∠A 是 AB 与 AC 的夹角，∠D 是 DE 与 DF 的夹角），则△ABC ≌ △DEF（SAS）。

4. 直角三角形的特殊判定：斜边直角边（HL）

（注：课本虽未单独列节，但在后续应用中会涉及，需提前掌握）

内容：斜边和一条直角边分别相等的两个直角三角形全等（简记 “HL”，仅适用于直角三角形）。

原因：直角三角形已有一个直角相等（90°），结合 “斜边 + 一条直角边”，可通过勾股定理推出第三条直角边也相等，本质是 SSS 的特殊情况。

示例：在 Rt△ABC 和 Rt△DEF 中，∠C=∠F=90°，若 AB=DE（斜边）、BC=EF（直角边），则 Rt△ABC ≌ Rt△DEF（HL）。

四、第 4 节：三角形的尺规作图

核心任务：用圆规和无刻度的直尺，根据给定条件作三角形（作图步骤需规范，保留作图痕迹）。

常见作图类型：

已知三边作三角形（依据 SSS）；

已知两角及其夹边作三角形（依据 ASA）；

已知两边及其夹角作三角形（依据 SAS）；

已知直角、斜边和一条直角边作直角三角形（依据 HL）。

关键要求：作图后需简要说明 “所作三角形即为所求”，并明确标注顶点。

五、第 5 节：利用三角形全等测距离

核心思想：将 “无法直接测量的距离” 转化为 “可通过全等三角形对应边相等的距离”（即 “转化思想”）。

经典示例：

测量池塘两端 A、B 的距离：在平地上取一点 C，连接 AC、BC 并延长，使 CD=AC、CE=BC，连接 DE，测量 DE 的长度即为 AB 的长度（依据 SAS：△ABC ≌ △DEC，故 AB=DE）。

解题步骤：① 构造全等三角形；② 证明三角形全等；③ 利用全等性质（对应边相等）得出测量结果。

总结：第一章 “三角形” 的高频考点与易错点

高频考点：三角形内角和定理、三边关系、三条重要线段（高、中线、角平分线）的性质、全等三角形的性质与判定（SSS、ASA、AAS、SAS、HL）、利用全等测距离。

易错点：

全等三角形的 “对应关系”（找错对应边 / 角，导致结论错误）；

误用 SSA 判定一般三角形全等；

直角三角形作图或判定时，忽略 “直角” 条件；

三角形高的位置（尤其钝角三角形的外高）判断错误。