中考数学：选择填空解答共计10道经典练习题详解

1. (单项选择题）2004的相反数是（ ）

A.2004 B. -2004 C. 1/2004 D. -1/2004

【答案】B.

【解析】：本题主要考查相反数的定义，解题的关键是熟练掌握正数相反数的定义。对于任意一个正数a，则其相反数为-a。

对于本题，a=2004,所以a的相反数为：-2004。

所以本题选择答案B.

2.(单项选择题）矩形ABCD内接于☉o，分别以AB、BC、CD、AD为直径向外作半圆，若AB=10,BC=13，则阴影部分的面积是（ ）。

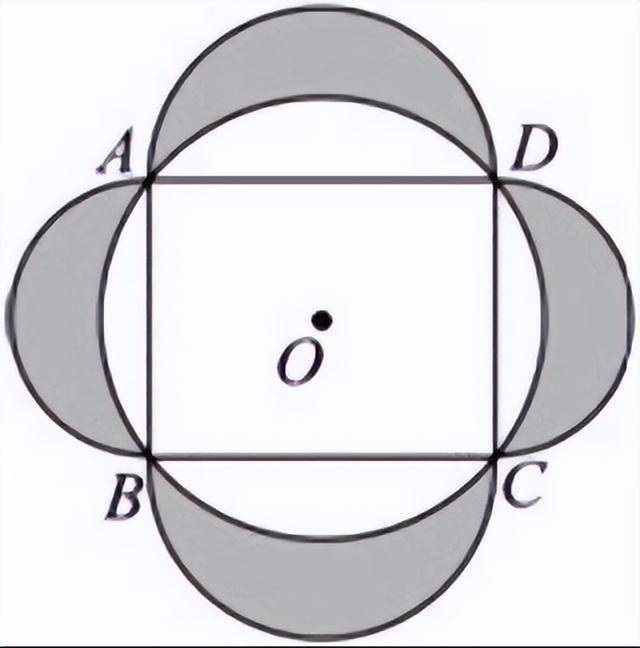
A.65/π-130 B.130/π-130 C. 130 D.130π

【答案】C.

【解析】本题考查了勾股定理，矩形的性质，根据阴影部分面积为2个直径分别为AB,BC的半圆的面积加上矩形的面积减去以矩形对角线AC长为直径的圆的面积即可求解．

解：如图所示，连接，矩形内接于☉o，AC为Rt△ABC的斜边。

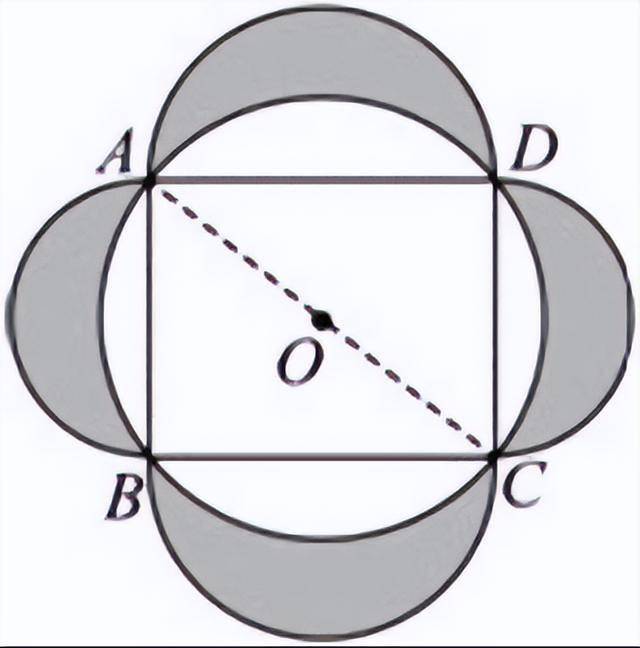
∴AC²=AB²+BC²，

∴阴影部分的面积为：

S阴影=S矩形ABCD+π*(AB/2)²+π*(BC/2)²-π*(AC/2)²

=S矩形ABCD+π*(1/4)(AB²+BC²-AC²)

=S矩形ABCD+0

=10*13=130平方单位.

3. (单项选择题）如图，在菱形ABCD中，AB=26，∠ABC=60°，M是对角线BD上的一个动点，CF=BF，则MA+MF的最小值为（ ）

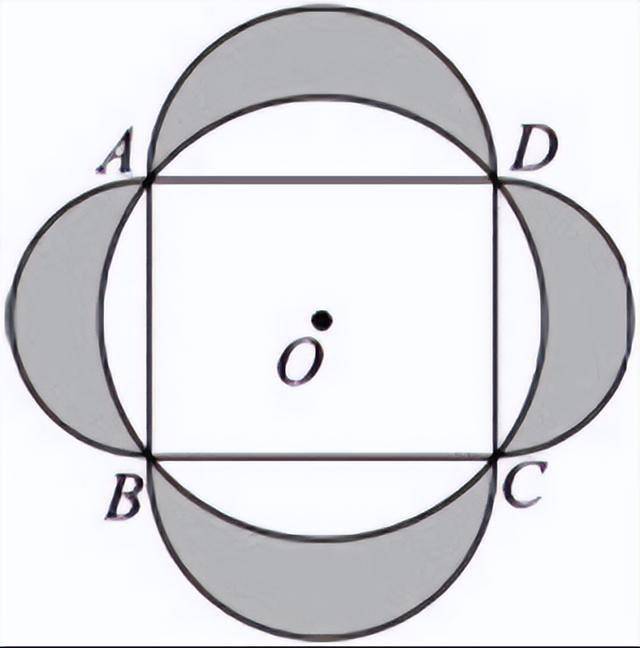
A.13 B.13√2 C.13√3 D.26

【答案】C.

【解析】本题考查了菱形的性质，等边三角形以及三角函数，确定AF的长就是MA+MF的最小值是关键。

解：连接AF，则AF的长就是AM+FM的最小值。

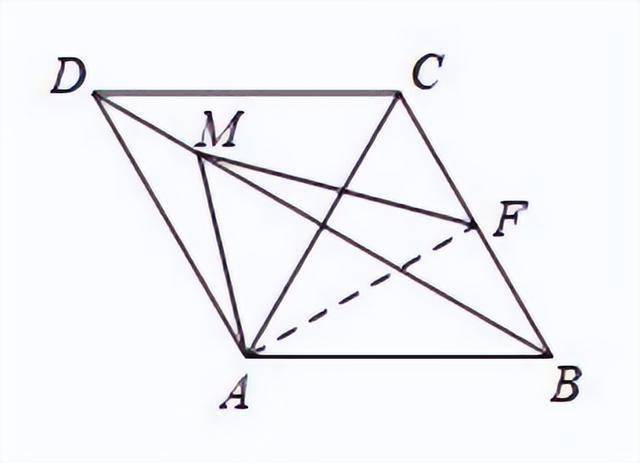
∵四边形ABCD是菱形，

∴AB＝BC，

又∵∠ABC＝60°，

∴△ABC是等边三角形，

∵CF=BF,

∴F是BC的中点，

∴AF⊥BC．

则AF＝AB•sin60°＝26*√3/2=13√3．

即MA+MF的最小值是13√3．

4. (填空题）分解因式：1600x²-9y²=________．

【答案】(40x+3y)(40x-3y）。

【解析】本题主要考查了利用平方差公式分解因式，熟记平方差公式是解题的关键．

解：1600x²-9y²

=40²x²-3²y²

=(40x)²-(3y)²

=(40x+3y)(40x-3y）。

5. (填空题）若2/√(77x-37)在实数范围内有意义，则实数x的取值范围是________．

【答案】x>37/77.

【详解】本题考查分式有意义条件和二次根式有意义的条件，熟练掌握分式有意义条件：分母不等于0，二次根式有意义的条件：被开方数为非负数．

根据分式有意义条件和二次根式有意义的条件得:

2/√(77x-37)≠0,且77x-37≥0,

所以：77x-37>0，

解得：x>37/77。

6. (填空题）如果正n边形的一个内角与一个外角的比是5：2，则n=_______．

【答案】n。

【解析】本题考查了多边形的内角、外角的知识和外角和定理，理解一个多边形的一个内角与它相邻外角互补是解题的关键。

设多边形的一个内角为5x度，一个外角则为2x度，求得外角的度数，然后根据多边形的外角和为360°，进而求出n的值．

解：正边形的一个内角度数与其外角度数的比是5：2，设多边形的一个内角为5x度，一个外角则为2x度，则：

∴5x+2x＝180°，解得x＝180°/7，

∴一个外角为2x＝(2/7)*180°,

360°÷[(2/7)*180°]＝2*7/2，

∴n＝7。

7. (填空题）若t²-2t-65=0,则代数式[t-(4t-4)/t]·[t²/(t-2)]的值是________．

【答案】65。

【解析】本题考查分式化简求值，需要掌握分式混合运算。先按分式混合运算法则化简分式，再把已知变形为t²-2t=65，整体代入即可．

解：[t-(4t-4)/t]·[t²/(t-2)]

=[t²-(4t-4)]/t·[t²/(t-2)]

=t[t²-(4t-4)]/(t-2)

=t(t-2)²/(t-2)

=t(t-2)

=t²-2t=65.

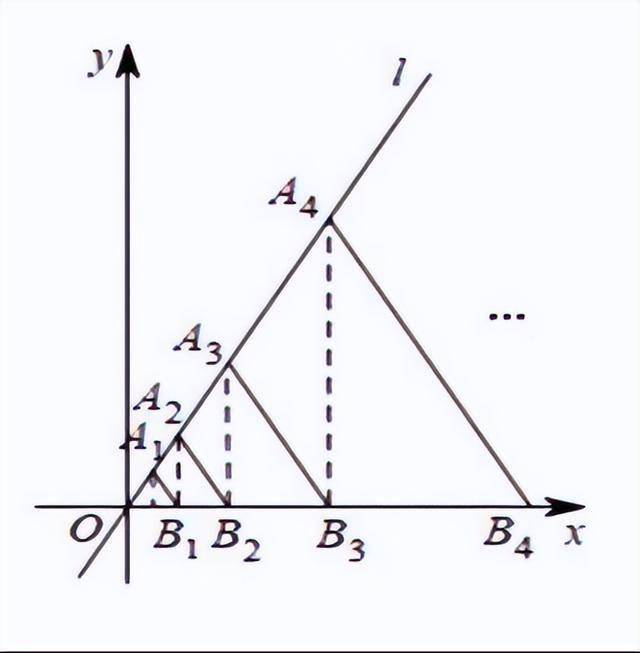
8. 如图，在第一象限内的直线L:y=√3x，上取点A₁，使OA₁=3，以OA₁为边作等边△OA₁B₁，交x轴于点B₁；过点B₁作x轴的垂线交直线L于点A₂，以OA₂为边作等边△OA₂B₂，交x轴于点B₂；过点B₂作x轴的垂线交直线L于点A₃，以OA₃为边作等边△OA₃B₃，交x轴于点B₃；……，依次类推，则点A2011的横坐标为_______．

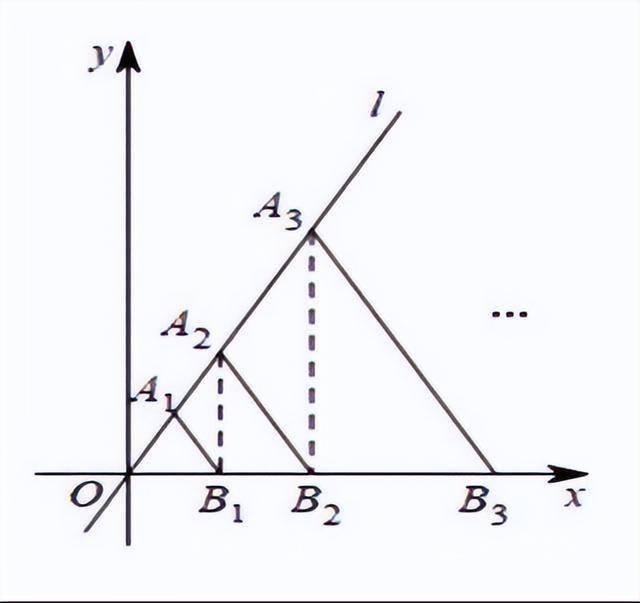
【答案】3*22009。

【详解】本题考查一次函数图像上点的坐标特征，等边三角形的性质，等腰三角形的三线合一性质，关键是找出点Aₙ的横坐标的变化规律。

根据一次函数图像上点的坐标特征和等边三角形的性质及等腰三角形的三线合一性质，得出：点A₁的横坐标为3*2⁻¹，点A₂的横坐标为3*2⁰，点A₃的横坐标为3*2¹，点A₄的横坐标为3*2²，找出规律即可求解．

解：过点A₁作A₁C⊥X轴于点，点B₃作B₃A₄⊥X轴交直线L于点A₄，

∵△OA₁B₁是等边三角形，OA₁=3，

∴A₁B₁=OB₁=OA₁=3，

∴OC=1/2*OA₁=1/2*3，

∴点A₁的横坐标为1/2*3，即3*2⁻¹，

∵△OA₂B₂是等边三角形，A₂B₁⊥X轴，OB₁=3，

∴点A₂的横坐标为3，即3*2⁰，OA₂=A₂B₂

∴OB₂=2*OB₁=2*3=3*2，

∵△OA₃B₃是等边三角形，A₃B₂⊥X轴，

∴点A₃的横坐标为3*2，即3*2¹，OA₃=A₃B₃,

∴OB₃=2*OB₂=2*3*2=3*4，

∵△OA₄B₄是等边三角形，A₄B₃⊥X轴轴，

∴点A₄的横坐标为3*4，即3*2²，

以此类推，点Aₙ的横坐标为3*2ⁿ⁻²，

∴当n=2011时，点A2011的横坐标为3*22009．

9. (解答题）计算：

(1/12)⁻¹+6cos45°-√18+(335-π)⁰．

【答案】13。

【解析】本题考查实数的混合运算，需要熟练掌握负整指数幂与零指数幂运算法则。计算过程为，先计算乘方和化简二次根式，并把特殊三角函数值代入，再合并同类二次根式，即可求解．

(1/12)⁻¹+6cos45°-√18+(335-π)⁰

=12+6cos45°-√18+1

=12+3√2-3√2+1

=12+1

=13.

10. (解答题）某健身器材店计划购买一批篮球和排球，已知每个篮球进价是每个排球进价的2.5倍，若用8250元购进篮球的数量比用6600元购进排球的数量少30个．

(1)篮球、排球的进价分别为每个多少元?

(2)该健身器材店决定用不多于58905元购进篮球和排球共300个进行销售，最多可以购买多少个篮球?

【答案】(1)每个篮球的进价为275元，每个排球的进价为110元．(2)143个.

【解析】本题考查了一元一次不等式的应用，分式方程的应用.(1)设每个排球的进价为x元，则每个篮球的进价为1.5x元，根据“用8250元购进篮球的数量比用6600元购进排球的数量少30个”得到方程；即可解得结果。（2）设健身器材店可以购进篮球a个，则购进排球(300﹣a）个，根据题意得不等式组即可得到结果．

(1)解:设每个排球的进价为x元，则每个篮球的进价为2.5x元

根据题意得8250/2.5x=6600/x-30．

解得x＝110．

经检验x＝110是原分式方程的解．

∴2.5x＝275（元）．

∴篮球的进价为110元，排球的进价为275元.

答：每个篮球的进价为110元，每个排球的进价为275元．

(2)设该体育用品商店可以购进篮球m个，则购进排球（300-m )个，根据题意，得110m+275(300-m)≤58905．

解得m≤143．

答：该健身器材店最多可以购进篮球143个．