人教A版数学（必修 第二册）电子课本可以方便大家随时随地预习或复习课本知识，为此，我们找到了人教A版数学（必修 第二册）新教材电子书教材的全部内容，以高清图片的形式呈现给大家，希望能够提高大家的学习效率。

如需全套电子课本PDF版，请关注公众号“桃李百科”回复：“电子课本”

人教A版数学（必修 第二册）新教材电子课本在线阅读（此为截图版，获取是高清版）

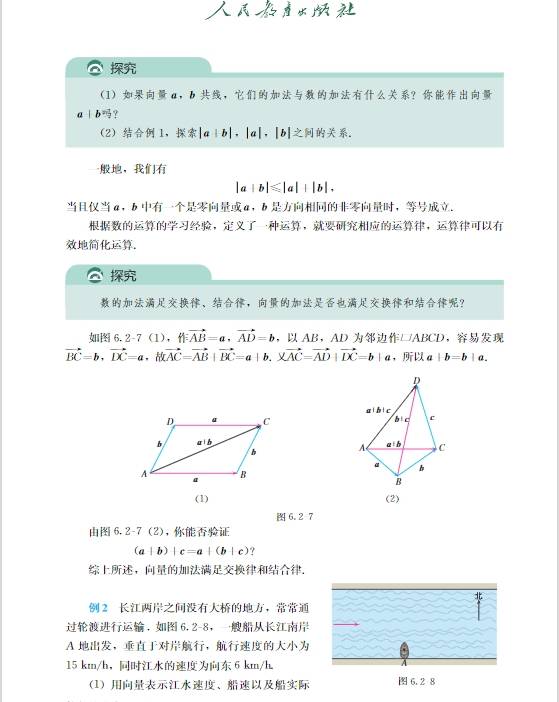
以下是对 2025 新教材人教 A 版高中数学必修第二册各单元更为详细的总结：

第六章 平面向量及其应用

• 知识结构：从向量的基本概念入手，引入向量的加法、减法、数乘运算，进而研究向量的数量积，最后将向量应用于几何与物理问题中。
• 重点内容：理解向量的概念，掌握向量的线性运算和数量积运算规则，能熟练运用向量的坐标表示进行运算。如通过向量的坐标运算判断向量的平行、垂直关系，计算向量的模长和夹角等。
• 难点突破：向量的概念较为抽象，需结合实例理解其几何意义和物理意义。在解决向量的综合应用问题时，要善于将几何问题转化为向量问题，利用向量的运算和性质进行求解。
• 实际应用：在物理中，可用于力的合成与分解、物体的位移和速度等问题的分析；在几何中，可证明平行、垂直关系，求解角度和长度等问题，为解决几何问题提供了新的方法和思路。

第七章 复数

• 知识结构：首先介绍复数的基本概念，包括虚数单位和复数的代数形式，然后学习复数的四则运算，最后探讨复数的三角表示及其应用。
• 重点内容：掌握复数的概念、运算规则和三角表示，理解复数的模、共轭复数等概念，能熟练进行复数的四则运算和三角形式与代数形式的相互转换。
• 难点突破：复数的概念和运算较为抽象，需要通过大量的练习来熟练掌握。复数的三角表示在几何意义和应用方面较难理解，可结合图形和实例进行学习。
• 实际应用：在电学中，用于交流电的分析和计算；在信号处理领域，可进行信号的调制和解调等；在几何变换中，利用复数的三角形式可方便地描述平面图形的旋转、伸缩等变换。

第八章 立体几何初步

• 知识结构：先认识柱、锥、台、球等简单空间几何体的结构特征，再学习空间几何体的表面积和体积公式，最后研究空间点、线、面的位置关系。
• 重点内容：掌握空间几何体的结构特征、表面积和体积公式，以及空间点、线、面位置关系的判定和性质定理，能运用这些知识进行空间几何体的相关计算和证明。
• 难点突破：需要较强的空间想象能力，可通过观察实物、模型和绘制图形等方式来提高。在证明空间位置关系时，要熟练运用公理、定理进行逻辑推理，注意推理的严谨性。
• 实际应用：在建筑设计、机械制造、工程测量等领域有着广泛的应用，如计算建筑物的体积和表面积、设计机械零件的形状和尺寸等。