2025年学生将迎来新版教材，新教材将更加重视思维和阅读！为了方便广大学生在暑假预习新学期的课本知识，我们整理了2025新

浙教版八年级数学（全册）一电子课本，以图片的形式呈现给大家，希望对同学们的暑期学习有所帮助。

以下是部分内容截图，完整信息请查看 PDF 文件

八年级数学在初中数学学习中起着承上启下的关键作用，知识点正从具体的运算向抽象的逻辑转变（例如函数概念），从单一的知识向综合的应用拓展（比如几何证明与代数运算相结合）。下面将从核心模块的特点、有针对性的学习方法以及习惯养成这三个维度，为大家分享具体的学习思路：

一、明确核心模块，实现针对性突破

八年级数学主要包含几何证明、代数运算、函数初步这三大模块，每个模块的学习重点和方法都有明显差异，需要精准发力。

1. 几何模块（全等三角形、轴对称、勾股定理、平行四边形）

核心内容：以 “证明” 为核心，涉及图形的性质、判定定理以及逻辑推理。学习思路：

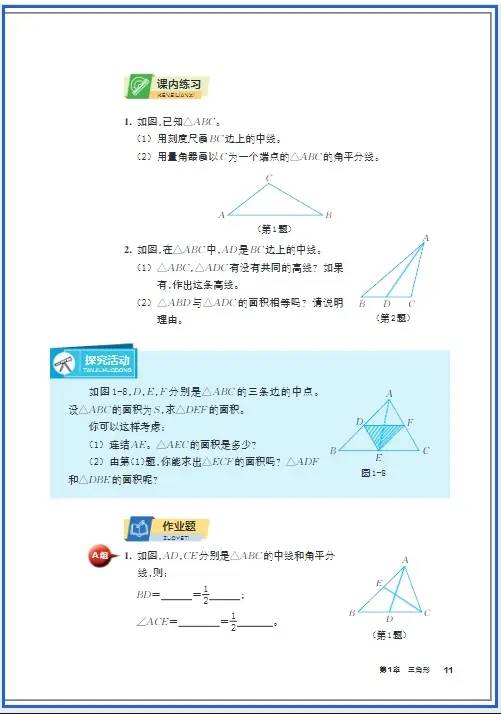
吃透 “概念 + 图形”：几何学习离不开图形，首先要熟记基本概念（像全等三角形的 “对应边相等、对应角相等”）、性质（如轴对称图形的 “对称轴垂直平分对应点的连线”）和判定定理（例如全等三角形的 “SAS、ASA、SSS”），并且要结合图形来理解（比如画出两个全等三角形，标注出对应边、角，直观地感受定理的含义）。

规范 “证明逻辑”：几何证明的每一步都要有 “依据”（如 “∵AB=CD（已知），∠A=∠C（已知），AC=CA（公共边），∴△ABC≌△CDA（SAS）”）。刚开始可以从 “填空式证明” 入手，逐渐过渡到独立书写证明过程，避免出现 “跳步” 或 “没有依据的推理”。

掌握 “辅助线技巧”：几何学习的难点常常在于辅助线的添加，需要总结常见的场景：

全等三角形：遇到中线可以 “倍长中线”（构造全等三角形）；遇到线段的和差可以 “截长补短”（比如要证明 AB=CD+EF，可以在 AB 上截取一段等于 CD，再证明剩余部分等于 EF）。

轴对称：求解最短路径（如 “牧马饮水” 问题），需要利用 “对称点” 来转化线段（对称轴上的一点到两个对称点的距离相等）。

1. 代数模块（整式乘除、因式分解、分式、二次根式）

核心内容：以 “运算” 为核心，涉及公式的应用、变形以及化简。学习思路：

攻克 “公式与法则”：代数运算的基础是公式，要精准记忆并且区分容易混淆的公式（如完全平方公式

(aA

^

±b)2

=a2

A

^

±2ab+b2

，避免漏掉中间项 “2ab”；平方差公式

(a+b)(a−b)=a2

−b2

，要注意符号）。

强化 “逆向思维”：因式分解是整式乘法的逆运算，要熟练掌握 “正向运用公式”（如

(x+2)(x−2)=x2

−4

）和 “逆向运用公式”（如

x2

−4=(x+2)(x−2)

），掌握 “一提（提取公因式）二套（套用公式）三查（检查是否分解彻底）” 的步骤。

规避 “运算陷阱”：分式运算要注意 “分母不能为 0”（解分式方程必须验根）；二次根式要注意 “被开方数是非负数”（如

x−1

中

xa

^

¥1

），避免因为忽略限制条件而出错。

1. 函数模块（一次函数）

核心内容：以 “数形结合” 为核心，理解变量之间的关系、图像的性质以及实际应用。学习思路：

从 “具体到抽象” 理解概念：函数的本质是 “两个变量之间的对应关系”（如 “路程 = 速度 × 时间” 中，当速度固定时，路程随着时间的变化而变化）。可以通过具体的例子（如列表记录 “时间 t 和温度 y” 的关系），逐步抽象出 “函数” 的定义。

用 “图像” 串联性质：一次函数

y=kx+bı

¨

¼ka

^

0ı

¨

¼

的关键在于 “k 和 b 的意义”：

k 决定 “增减性”（当

k>0

时，y 随着 x 的增大而增大；当

k<0

时则相反）；

b 决定 “与 y 轴的交点”（坐标为

(0,b)

）；

一次函数的图像是 “直线”，画图像时只需要找出两个点（如与 x 轴、y 轴的交点）。建议多画图进行对比：比如画出

y=2x

、

y=2x+3

、

y=−2x+3

的图像，直观地感受 k 和 b 对图像的影响。

结合 “实际问题” 建模：一次函数常常用于解决 “行程问题”（如相遇、追及问题）、“利润问题”（如销量与利润的关系），需要学会从题干中提取 “变量”（设 x、y），找到等量关系列出表达式，再结合图像或性质进行求解。

二、通用能力培养：从 “做题” 到 “懂逻辑”

八年级数学难度提升的核心在于 “逻辑复杂度增加”，需要重点培养以下能力：

“因果推导” 能力：在做证明题时，要明确 “已知条件能推出什么”“要证明结论需要什么”，形成 “从已知到未知” 的链条（如要证明线段相等，可以考虑 “全等三角形对应边相等”“等腰三角形两腰相等” 等路径）。

“分类讨论” 意识：当问题存在多种可能性时，要全面分析（如等腰三角形已知两边长求周长，需要分 “腰长” 和 “底边长” 两种情况，而且要满足 “三角形三边关系”）。

“错题归因” 习惯：对于错题，不仅要改正答案，更要记录 “错误类型”：

概念错误（如混淆 “全等” 与 “相似”）；

公式错误（如因式分解时漏项）；

逻辑错误（如证明步骤没有依据）；定期复习错题，避免重复犯错。

三、日常学习习惯：避免 “夹生饭”

预习抓住 “重点”：提前看课本，标记出 “不懂的概念”（如 “函数的定义”）和 “复杂公式”（如分式的通分法则），带着问题听课，效率会更高。

复习做到 “当天清”：每天花 10 分钟回顾课堂内容，用 “思维导图” 梳理知识点（如 “全等三角形” 包含 “定义、性质、判定、辅助线”），避免知识点堆积。

练习追求 “少而精”：优先做教材例题和课后题（基础题），再做中档题（综合应用题），难题可以暂时跳过，确保基础题 “零失误”（如整式运算、分式化简）。

八年级数学学习的关键在于 “稳”—— 基础扎实、逻辑清晰、习惯良好，就能顺利过渡到九年级的综合应用。遇到难点不要慌张，逐个突破，积累到一定程度就会有 “豁然开朗” 的感觉！