北师大版九年级英语（上册） 电子课本可以方便大家随时随地预习或复习课本知识，为此，我们找到了北师大版九年级英语（上册） 新教材电子书教材的全部内容，以高清图片的形式呈现给大家，希望能够提高大家的学习效率。

如需全套电子课本PDF版，请关注公众号“桃李文库”回复：“电子课本”

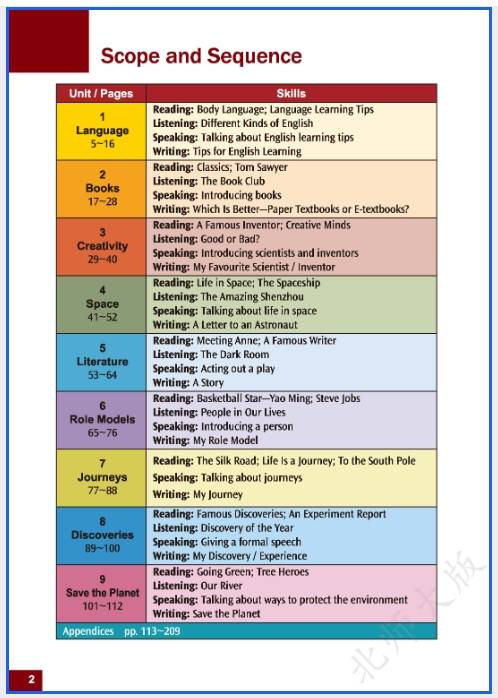
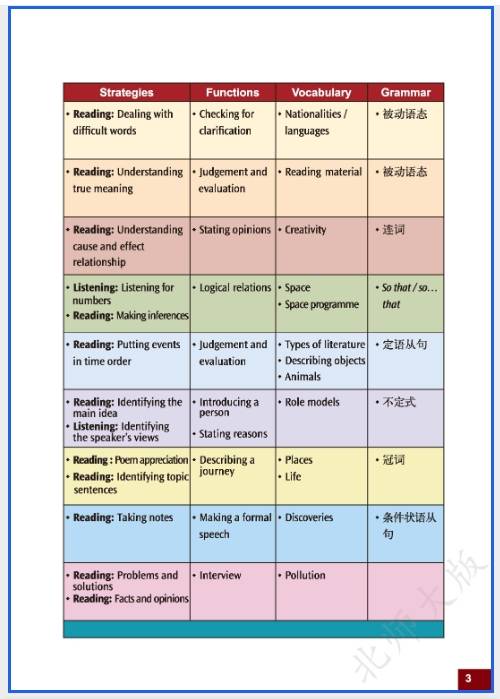
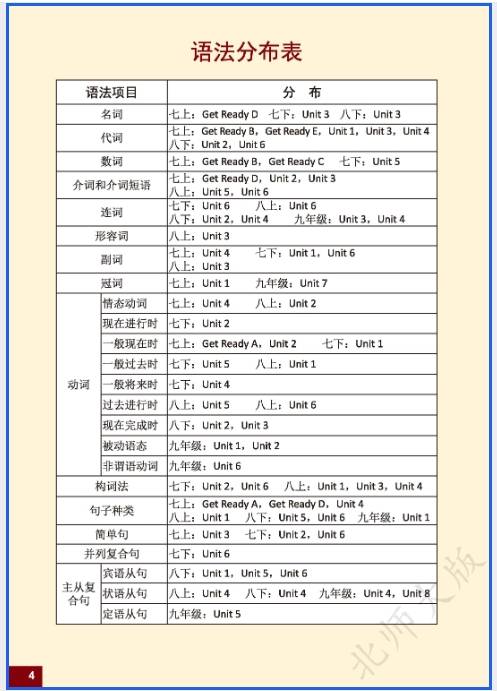
北师大版九年级英语（上册） 新教材电子课本在线阅读（此为截图版，获取是高清版）

九年级数学综合指南：知识、考情与提分策略

一、核心知识体系：三大领域的 “综合与深化”

九年级数学是初中知识的 “收官阶段”，在七、八年级基础上实现 “从单点到系统、从计算到建模” 的跨越，核心围绕 “数与代数”“图形与几何”“统计与概率” 三大领域展开，其中前两者是中考核心。

（一）数与代数：中考占比约 50%，压轴题核心载体

该领域以 “方程、函数、不等式” 为核心，强调 “代数运算与逻辑推理” 的结合，是九年级分值最高的模块。

1. 一元二次方程（九年级上册）

• 基础核心：
• 定义与形式：只含一个未知数、最高次项为 2 次的整式方程，一般式为\(ax²+bx+c=0\)（\(aâ 0\)）。
• 解法进阶：从 “直接开平方法、配方法” 到 “公式法（求根公式\(x=\frac{-b±\sqrt{b²-4ac}}{2a}\)）、因式分解法”，需根据方程特征选最优解法（如可因式分解优先用分解法，无法分解用公式法）。
• 高频考点：
• 根的判别式（\(\Delta=b²-4ac\)）：判断方程实根个数（\(\Delta>0\)有两不等实根；\(\Delta=0\)有两相等实根；\(\Delta<0\)无实根），常结合几何图形存在性问题考查（如 “抛物线与直线有两个交点” 需\(\Delta>0\)）。
• 根与系数的关系（韦达定理）：若方程两根为\(xâãxâ\)，则\(xâ+xâ=-\frac{b}{a}\)，\(xâxâ=\frac{c}{a}\)，用于求根的代数式值（如\(xâ²+xâ²=(xâ+xâ)²-2xâxâ\)）、构造新方程。
• 应用场景：增长率问题（如 “两年增长率为 20%，求年平均增长率”）、面积问题（如 “矩形场地改造成花坛，求边长”）、利润问题（如 “售价调整后求最大利润对应的定价”）。

2. 二次函数（九年级下册）

• 基础核心：
• 定义与表达式：形如\(y=ax²+bx+c\)（\(aâ 0\)）的函数，三种表达式各有妙用 —— 一般式（已知三点坐标）、顶点式\(y=a(x-h)²+k\)（已知顶点坐标或最值）、交点式\(y=a(x-xâ)(x-xâ)\)（已知与 x 轴交点）。
• 图像与性质：抛物线开口方向（\(a>0\)向上，\(a<0\)向下）、对称轴（\(x=-\frac{b}{2a}\)）、顶点坐标（\((-\frac{b}{2a},\frac{4ac-b²}{4a})\)）、增减性（以对称轴为界，\(a>0\)左减右增）。
• 高频考点：
• 图像变换：平移（“左加右减、上加下减”，如\(y=ax²\)平移到\(y=a(x-h)²+k\)）、对称（关于 x 轴、y 轴、原点对称的解析式转化）。
• 与一元二次方程的关系：抛物线与 x 轴交点横坐标即方程\(ax²+bx+c=0\)的根，结合判别式分析交点个数。
• 最值问题：利用顶点式求 “实际问题中的最大值 / 最小值”（如利润最大、面积最小），需注意自变量取值范围（如 “人数为正整数”）。
• 压轴关联：与几何图形综合（如 “抛物线上是否存在点，使构成的三角形为等腰 / 直角三角形”“抛物线与圆的位置关系”），需结合几何性质与代数运算求解。

3. 反比例函数（九年级上册）

• 基础核心：形如\(y=\frac{k}{x}\)（\(kâ 0\)）的函数，图像为双曲线，关于原点对称。
• 高频考点：
• 性质：\(k>0\)时双曲线在一、三象限，\(y\)随\(x\)增大而减小；\(k<0\)时在二、四象限，\(y\)随\(x\)增大而增大（注意 “在同一象限内” 的前提）。
• \(k\)的几何意义：过双曲线上任一点作 x 轴、y 轴垂线，围成的矩形面积为\(|k|\)，常考面积计算与\(k\)值求解。

（二）图形与几何：中考占比约 35%，逻辑推理核心

该领域以 “圆、相似、解直角三角形” 为新增核心，融合八年级几何知识，强调 “定理应用与辅助线构造”。

1. 圆（九年级上册 + 下册）

• 基础核心：圆的定义、圆心、半径、弦、弧（优弧 / 劣弧）、圆心角、圆周角等概念。
• 高频定理：
• 圆周角定理：同弧所对的圆周角等于圆心角的一半；直径所对的圆周角是直角。
• 垂径定理：垂直于弦的直径平分弦且平分弦所对的弧（及其推论，如 “平分弦的直径垂直于弦”）。
• 切线的判定与性质：切线垂直于过切点的半径（性质）；经过半径外端且垂直于半径的直线是切线（判定），常作为几何证明题核心考点。
• 计算核心：
• 弧长公式：\(l=\frac{nÏR}{180}\)（\(n\)为圆心角度数，\(R\)为半径）。