2025苏教版小学五年级数学上册电子课本(高清PDF版)
开心田螺
2025-09-30 14:08:25
0次
2025年学生将迎来新版教材,新教材将更加重视思维和阅读!为了方便广大学生在暑假预习新学期的课本知识,我们整理了2025新苏教版五年级数学(上册)一电子课本,以图片的形式呈现给大家,希望对同学们的暑期学习有所帮助。
以下是部分内容截图,完整信息请查看 PDF 文件








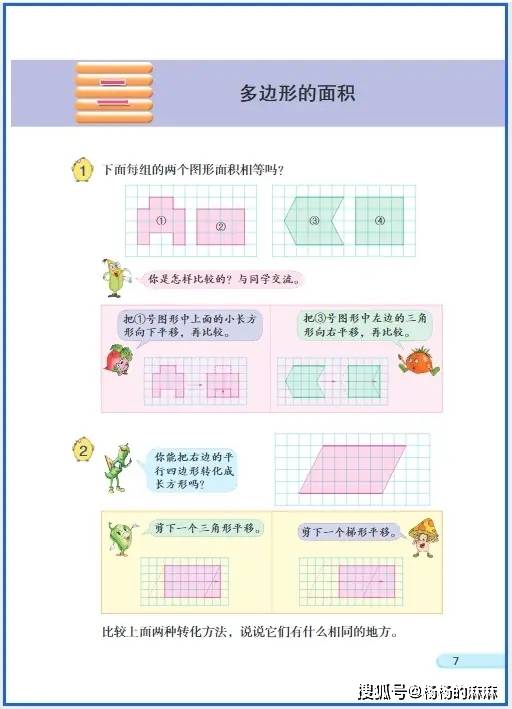

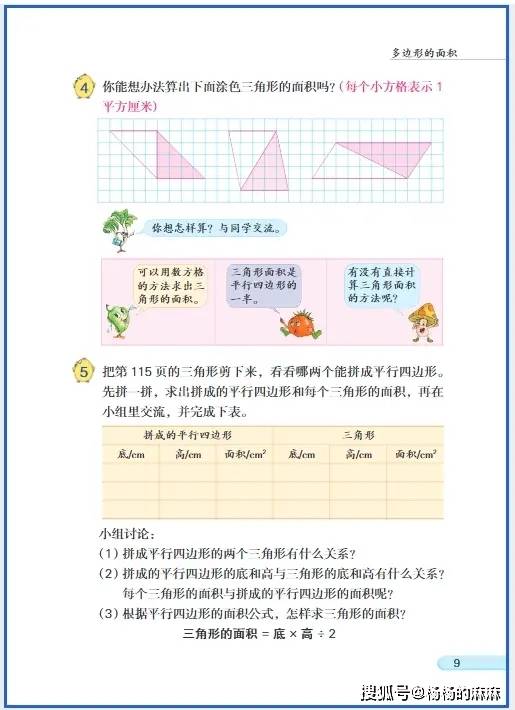

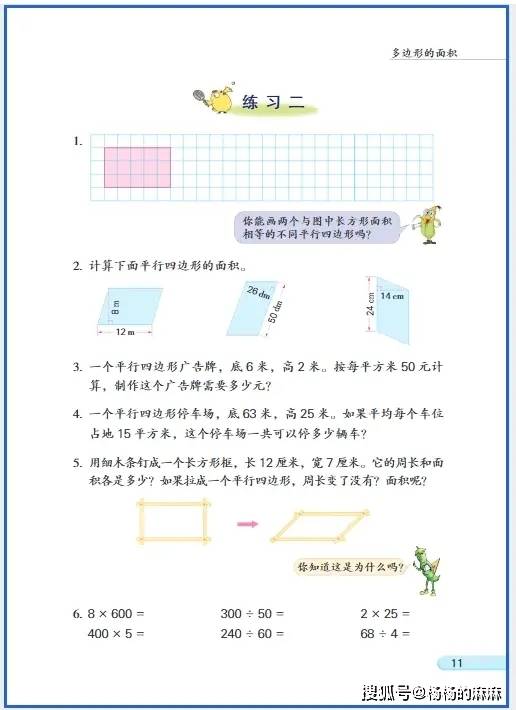
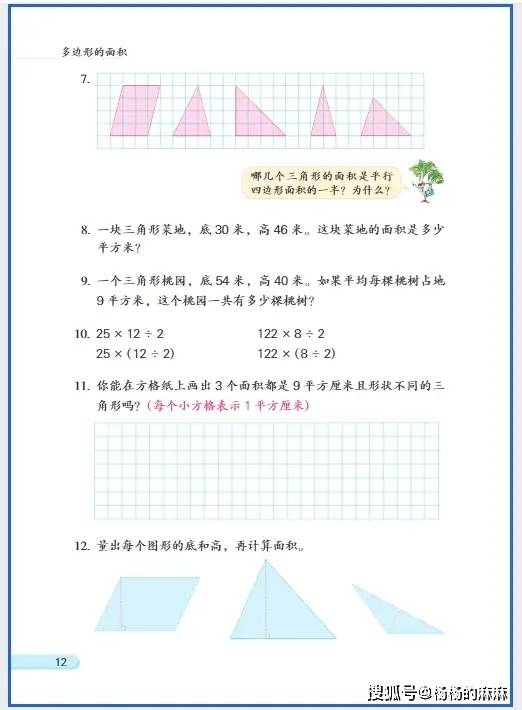
(一)小学阶段(1-6 年级):具象感知,构建基础认知
1. 数与运算
- 数的认知与运算融合:整数、小数、分数的意义理解及其四则运算,核心是把握相同计数单位的运算本质—— 如小数加减需对齐数位(本质是统一计数单位),分数乘法需理解 “单位分数的累加” 逻辑。
- 运算规律应用:加法交换律、结合律与乘法交换律、结合律、分配律的具象化运用,重点通过实际情境(如物品分装、路程计算)理解规律的实用价值,而非单纯记忆公式。
2. 图形与几何
- 图形的认识与测量:平面图形中长方形、正方形、三角形等的特征探索与度量计算,关键在于转化思想的渗透(如将平行四边形割补为长方形推导面积公式);立体图形聚焦长方体、正方体的特征认知,区分表面积(面的面积总和)与体积(空间占用大小)的度量本质,规避单位混淆问题。
- 图形与位置:初步掌握用有序数对描述点的位置,认识平移、旋转、轴对称等图形运动形式,感知运动过程中 “变与不变” 的特性。
3. 数量关系
- 典型问题建模:通过和差倍、行程、分数、工程等问题,提炼基本数量关系式(如路程 = 速度 × 时间),学会找准数量间的对应关系(如分数问题中的 “单位 1”),培养初步的模型意识。
(二)初中阶段(7-9 年级):抽象建模,强化逻辑推理
1. 代数与方程
- 数式运算进阶:整式运算围绕同类项合并与幂的运算法则展开,新增因式分解(提公因式法、公式法);分式运算强调分母非零的前提,核心是代数式的等价变形。
- 方程与不等式体系:一元一次方程侧重解法步骤的规范性(移项、合并同类项、系数化 1);二元一次方程组掌握代入消元与加减消元的本质逻辑;一元二次方程重点理解求根公式的推导过程及应用场景;不等式则需明确性质的约束条件(如乘除负数变号规则)。
2. 函数与关系
- 三类函数核心:一次函数(y=kx+b,k≠0)聚焦图像斜率与截距的意义(k 决定增减性);二次函数(y=ax²+bx+c,a≠0)侧重顶点坐标与开口方向的分析;反比例函数(y=k/x,k≠0)关注图像分布与变量变化规律,贯穿数形结合思想的深度应用。
3. 几何与证明
- 三角形体系:全等三角形的判定(SSS/SAS/ASA/AAS/HL)与性质用于线段、角的等量证明;相似三角形强调 “对应边成比例、对应角相等” 的本质,结合勾股定理解决直角三角形问题。
- 四边形与圆:平行四边形及特殊四边形(矩形、菱形、正方形)的性质与判定形成知识链条,通过边角关系实现转化;圆的知识围绕垂径定理、圆周角定理及切线性质展开,强化几何推理的严谨性。
4. 统计与概率
- 数据分析:掌握平均数、方差等统计量的计算与意义,学会从数据中提取信息;概率部分聚焦随机事件的可能性分析,通过树状图等工具梳理事件关系。
相关内容
热门资讯
英国本科留学伦敦传媒学院LCC...
伦敦艺术大学,简称UAL,坐落于英国伦敦,是专精于艺术、设计、时尚与表演教育的顶尖学府。 QS连续6...
1977年上海高考状元:公费留...
春风得意马蹄疾,一日看尽长安花。 中国有着通过考试改变命运的悠久传统。尤其是在如今竞争激烈的社会环境...
幼儿园收费新规!下月施行
📢📢📢 据国家发改委网站 12月23日 国家发展改革委 教育部 财政部 发布通知 完善幼儿园收费政策...
国务院学位委员会发文 做好博硕...
来源:人民日报 本报北京12月29日电 (记者黄超)国务院学位委员会近日印发《“博士+硕士”双学位项...
2025搜狐教育年度盛典在京成...
2025年12月29日,由搜狐网、搜狐教育主办的“2025搜狐教育年度盛典” 在北京成功举办。活动以...
深度实践儿童友好理念 打造幼有...
教育是国之大计,幼教是教育体系的根基。深圳市福田区西交利物浦大学基础教育集团外国语幼儿园(以下简称“...
成都名校名师齐聚七万通锦:同课...
12月25日至26日,中国陶行知研究会第五届“同上一节课”研讨活动聚焦“数智深融”主题,在成都七中万...
学前儿童均须建立学籍!教育部最...
12月29日 教育部发布 全国学前儿童学籍管理办法(试行) (以下简称《办法》) 进一步保障学前儿童...
巧下功夫提升小学数学教学成效
(来源:内蒙古日报) 转自:内蒙古日报 在小学数学小组合作教学中,教师若想提升成效,可在任务设计、互...
右江民族医学院举办新时代文明实...
右江民族医学院新时代文明实践所“师德讲堂”活动现场。陆怡如摄 “健康所系,性命相托,大医精诚抒写爱的...
