2025年学生将迎来新版教材，新教材将更加重视思维和阅读！为了方便广大学生在暑假预习新学期的课本知识，我们整理了2025新

冀教版九年级数学（上册）一电子课本，以图片的形式呈现给大家，希望对同学们的暑期学习有所帮助。

如需全套电子课本PDF版，请关注公众号“桃李科普”回复：“电子课本”

冀教版九年级数学（上册）电子课本在线阅读

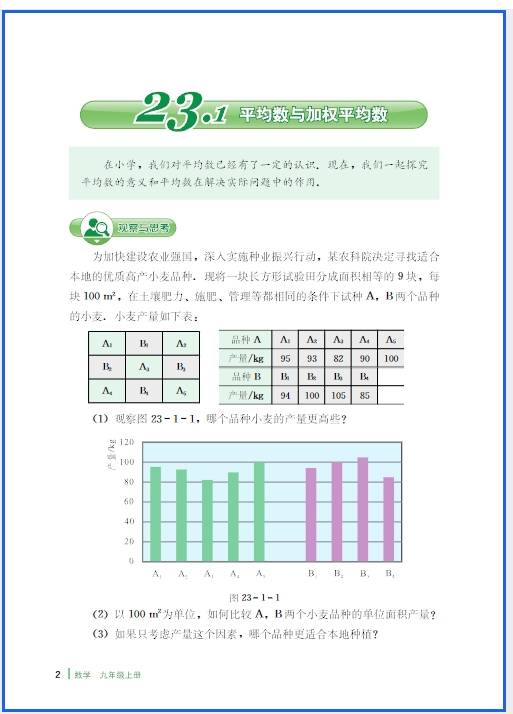
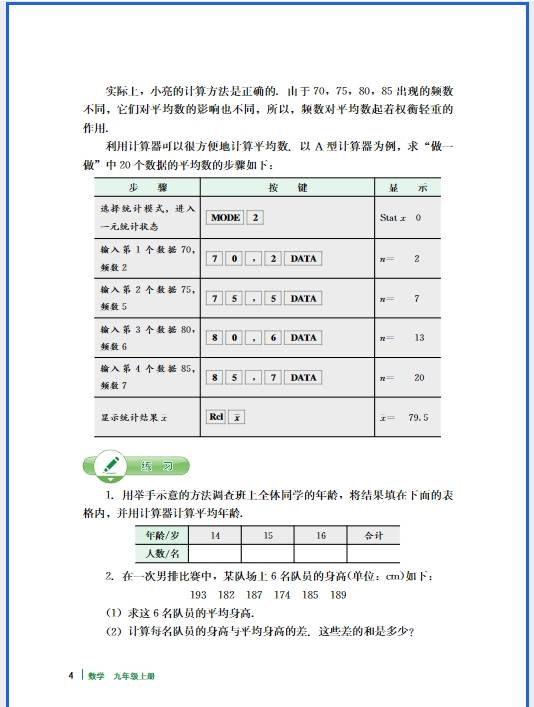
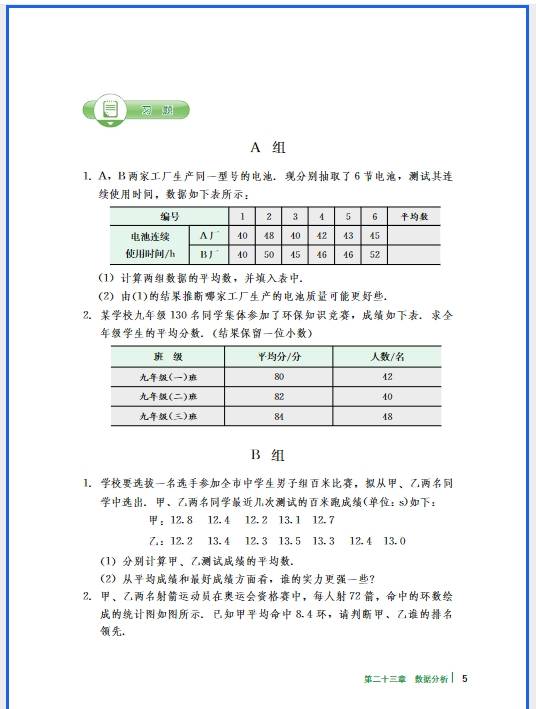
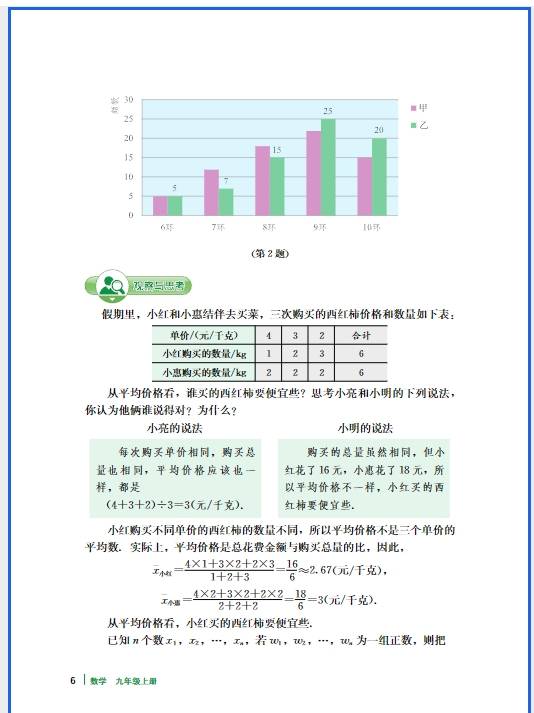
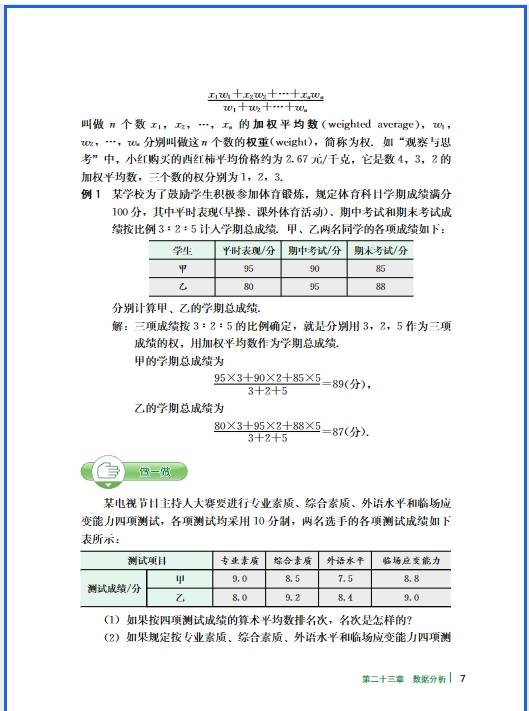
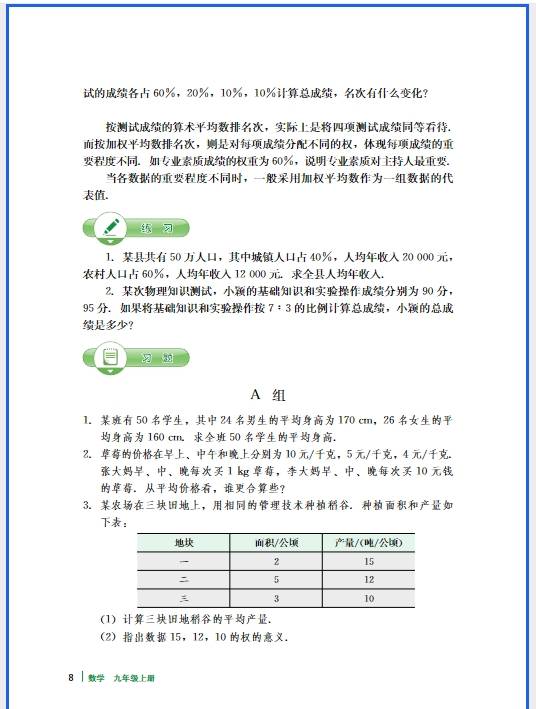
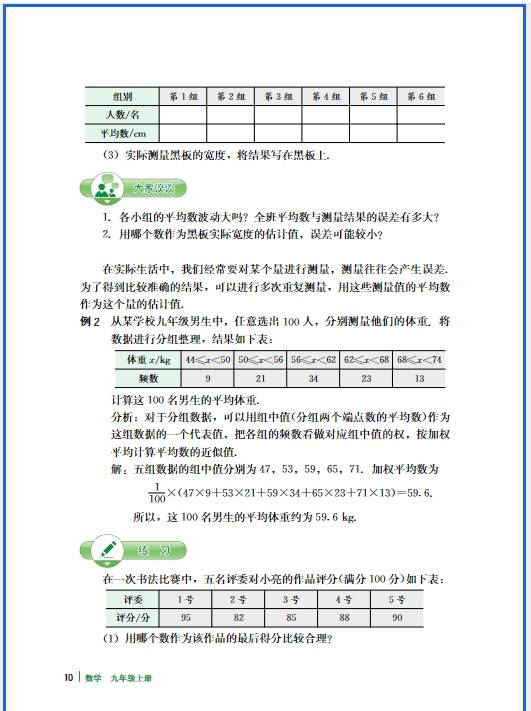
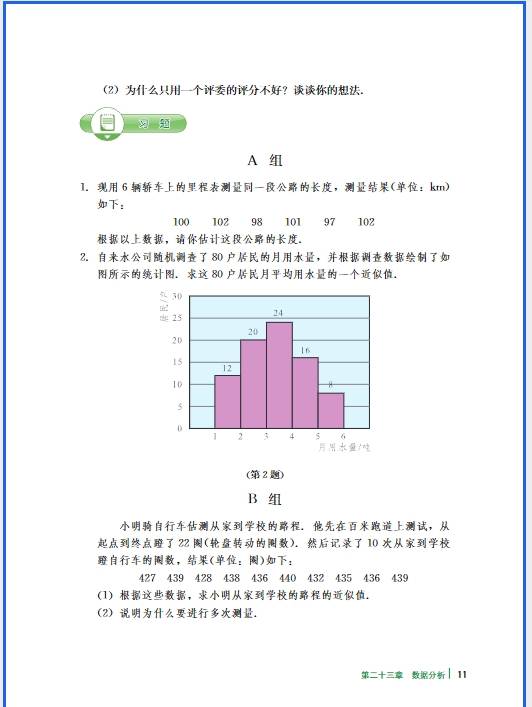
正比例函数的易错点集中在 “定义理解不透彻”“性质记忆混淆” 和 “实际应用忽略细节” 这三个方面，很多同学出错都是因为没抓住 “形如

y=kx

（

k



=0

）” 这个核心定义。

一、定义类易错点：漏掉 “

k



=0

” 或 “次数为 1”

正比例函数的严格定义是 “形如

y=kx

（

k

是常数，且

k



=0

）的函数”，两个条件缺一不可，容易忽略其中一个导致错解。

例题 1：判断函数

y=(m−2)x

m

2

−3

是否为正比例函数，求

m

的值。

错解：认为只要满足 “次数为 1”，即

m

2

−3=1

，解得

m=2

或

m=−2

，直接判定

m=±2

。

正解：需同时满足两个条件：

自变量次数为 1：

m

2

−3=1

，解得

m=2

或

m=−2

；

比例系数

k



=0

：

m−2



=0

，即

m



=2

；

综上，

m=−2

。

二、性质类易错点：混淆 “

k

的符号与增减性”

正比例函数的增减性由

k

的符号决定：

k>0

时，

y

随

x

增大而增大；

k<0

时，

y

随

x

增大而减小。容易记反符号与增减性的关系，或忽略 “在全体实数范围内” 的前提。

例题 2：已知点

A(1,y

1

、

B(3,y

2

在正比例函数

y=(1−2m)x

的图象上，且

y

1

>y

2

，求

m

的取值范围。

错解：因为

1<3

且

y

1

>y

2

，误认为 “

y

随

x

增大而增大”，所以

1−2m>0

，解得

m<

2

1

。

正解：

由

1<3

但

y

1

>y

2

，可知

y

随

x

增大而减小，对应

k<0

；

因此

1−2m<0

，解得

m>

2

1

。

三、图像类易错点：误解 “图像过原点” 或 “与坐标轴的交点”

正比例函数的图像是 “过原点（0,0）的直线”，容易和一次函数（

y=kx+b

，



=0

）混淆，错认为图像不过原点，或误判与坐标轴的交点数量。

例题 3：判断 “正比例函数

y=3x

的图像与

y

轴交于点（0,3）” 这句话是否正确。

错解：认为 “常数项是 3”，所以与

y

轴交点为（0,3），判定这句话正确。

正解：正比例函数

y=kx

中没有常数项（即

b=0

），图像必过原点（0,0），因此与

y

轴交点是（0,0），而非（0,3），这句话错误。

四、实际应用类易错点：忽略 “自变量的实际意义”

用正比例函数解决实际问题（如路程、面积）时，容易只关注函数表达式，而忽略自变量的实际取值范围（如长度不能为负、数量为正整数）。

例题 4：已知正方形的边长为

x

，周长为

y

，写出

y

与

x

的函数关系，并说明

x

的取值范围。

错解：函数关系为

y=4x

，认为

x

可取全体实数。

正解：

周长与边长的关系是

y=4x

，符合正比例函数定义；

实际中正方形边长为正数，因此

x

的取值范围是

x>0

（若题目有具体限制，需结合限制补充，如 “

x≤10

厘米”）。

要不要我帮你整理一份正比例函数 “易错点 + 例题 + 避坑技巧” 的总结表？把每个易错点的核心错误、正确思路和提醒都列出来，你复习时能更直观地避开这些 “坑”。