2025年学生将迎来新版教材，新教材将更加重视思维和阅读！为了方便广大学生在暑假预习新学期的课本知识，我们整理了2025人教小学数学五年级下册一电子课本，以图片的形式呈现给大家，希望对同学们的暑期学习有所帮助。

如需全套电子课本PDF版，请关注公众号“桃李科普”回复：“电子课本”

2025人教小学数学五年级下册电子课本在线阅读

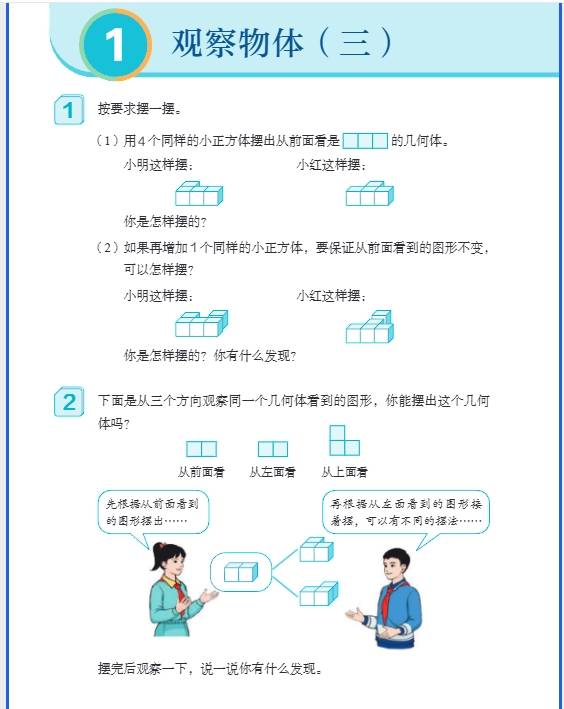
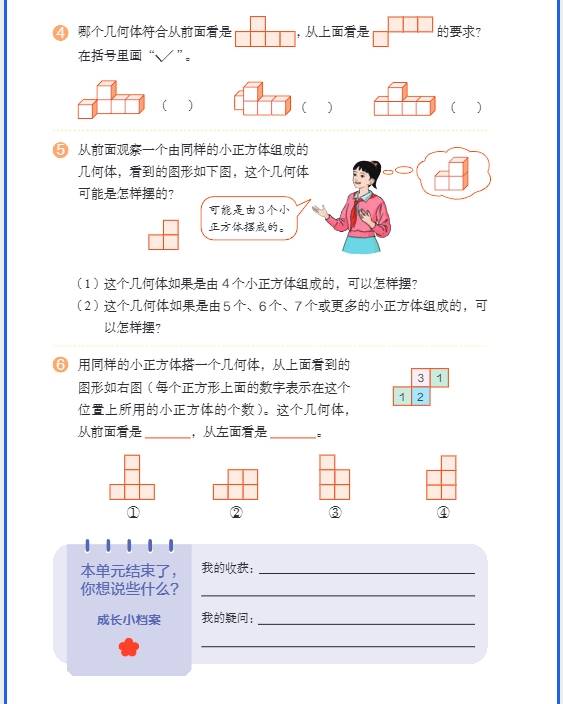
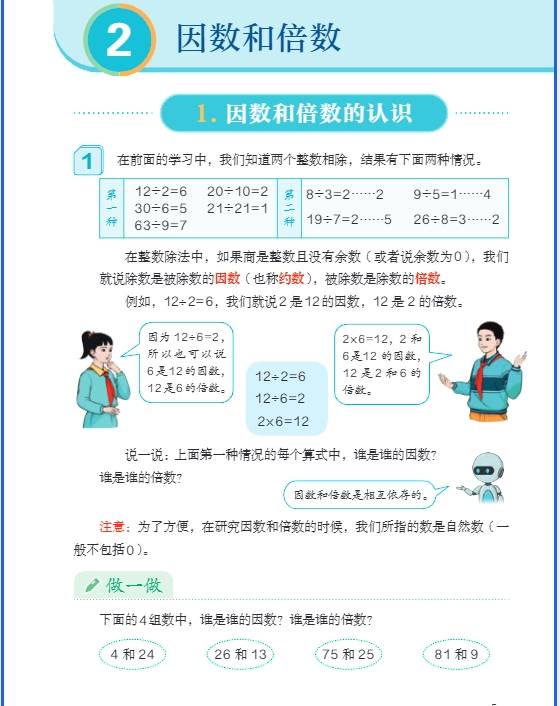
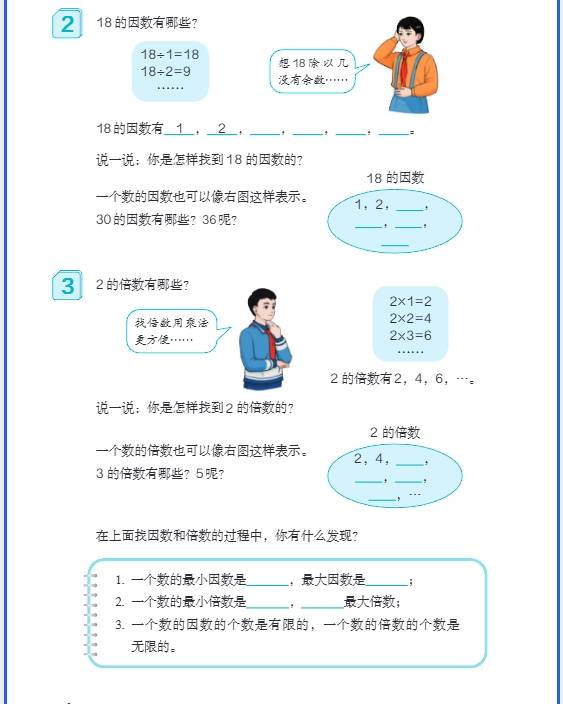
一、分数与百分数综合应用

1. 复杂分数计算

• 计算：\(\frac{1}{1\times2} + \frac{1}{2\times3} + \frac{1}{3\times4} + \cdots + \frac{1}{99\times100}\)
• 思路：利用裂项相消法，将每一项拆分为\(\frac{1}{n(n + 1)} = \frac{1}{n} - \frac{1}{n + 1}\)，原式可转化为\((1 - \frac{1}{2}) + (\frac{1}{2} - \frac{1}{3}) + \cdots + (\frac{1}{99} - \frac{1}{100}) = 1 - \frac{1}{100} = \frac{99}{100}\)。

1. 浓度问题

• 有含盐率为 15% 的盐水 200 克，要使盐水的含盐率变为 20%，需要蒸发掉多少克水？
• 解析：先算出盐的质量为\(200×15\% = 30\)克，蒸发水后盐的质量不变，此时盐水质量为\(30÷20\% = 150\)克，所以需要蒸发掉\(200 - 150 = 50\)克水。

二、几何图形拓展

1. 组合图形面积

• 如图，长方形 ABCD 的长为 8 厘米，宽为 6 厘米，三角形 ABE 的面积比三角形 DEF 的面积大 12 平方厘米，求 DF 的长度。
• 思路：因为三角形 ABE 的面积比三角形 DEF 的面积大 12 平方厘米，所以长方形 ABCD 的面积比三角形 BCF 的面积大 12 平方厘米。长方形面积为\(8×6 = 48\)平方厘米，则三角形 BCF 的面积为\(48 - 12 = 36\)平方厘米。又因为 BC = 6 厘米，根据三角形面积公式可得 CF 的长度为\(36×2÷6 = 12\)厘米，所以 DF = 12 - 8 = 4 厘米。

1. 立体图形体积

• 一个长方体，如果高增加 2 厘米就变成了一个正方体，且表面积比原来增加了 56 平方厘米。求原来长方体的体积。
• 解析：高增加 2 厘米变成正方体，说明长和宽相等且比高大 2 厘米。增加的表面积是 4 个同样的长方形的面积和，一个面的面积为\(56÷4 = 14\)平方厘米，长方形的长（即正方体棱长）为\(14÷2 = 7\)厘米，原来长方体的高为\(7 - 2 = 5\)厘米，体积为\(7×7×5 = 245\)立方厘米。

三、方程与函数思想

1. 列方程解应用题

• 甲、乙两车同时从 A、B 两地相向而行，在距 A 地 80 千米处相遇，相遇后两车继续前进，甲车到达 B 地、乙车到达 A 地后均立即按原路返回，第二次在距 B 地 60 千米处相遇。求 A、B 两地间的路程。
• 设 A、B 两地间的路程为 x 千米：第一次相遇时，甲走了 80 千米，两人共走了一个全程 x；第二次相遇时，两人共走了三个全程 3x，因为速度不变，所以甲走的路程是第一次相遇时的 3 倍，即\(80×3 = 240\)千米。又因为第二次相遇时甲走的路程为一个全程加 60 千米，可列方程\(x + 60 = 240\)，解得\(x = 180\)千米。

1. 函数规律探索

• 观察下表，找出 x 与 y 的关系并填写空格。

x | 1 | 2 | 3 | 4 | 5 |

---|---|---|---|---|---|

y | 3 | 7 | 13 | 21 | （ ） |

• 规律：\(y = x^2 + x + 1\)，当\(x = 5\)时，\(y = 5^2 + 5 + 1 = 31\)。

四、逻辑推理与策略

1. 复杂逻辑推理

• 甲、乙、丙、丁四人参加数学竞赛，赛后他们四人预测名次的谈话如下：

甲：“丙第一名，我第三名。”

乙：“我第一名，丁第四名。”

丙：“丁第二名，我第三名。”

丁没有说话。最后公布结果时，发现他们每人都只说对了一半。请你说出这次竞赛四人的名次。

• 假设甲说的 “丙第一名” 是正确的：那么丙说的 “我第三名” 就是错误的，“丁第二名” 就是正确的；乙说的 “丁第四名” 就是错误的，“我第一名” 就是正确的，这与 “丙第一名” 矛盾，所以此假设不成立。因此甲说的 “我第三名” 是正确的，丙说的 “我第三名” 错误，“丁第二名” 正确；乙说的 “丁第四名” 错误，“我第一名” 正确，剩下丙就是第四名。所以名次为：乙第一，丁第二，甲第三，丙第四。

1. 博弈策略问题

• 有 100 根火柴，甲、乙两人轮流取，规定每次可取 1 - 10 根火柴，谁取到最后一根谁就获胜。如果甲先取，甲第一次取几根才能保证获胜？
• 策略：因为每次可取 1 - 10 根，所以两人一轮最多取\(10 + 1 = 11\)根。\(100÷11 = 9\cdots\cdots1\)，甲先取 1 根，然后每次乙取 n 根（\(1\leq n\leq10\)），甲就取\(11 - n\)根，这样甲就能取到最后一根获胜。