数学学习的重要性已经不言而喻。而数学史的认识也逐渐被大家所重视。

数学学习赋予我们认识世界、改造世界的强大理性工具和思维能力；数学史学习则赋予这些工具和思想以灵魂、温度和深度，让我们理解数学作为人类伟大文化成就的来龙去脉、内在动力和人文价值。 两者结合，才能培养出既具有强大逻辑分析能力和解决问题能力，又具有深厚人文素养、批判性思维和历史视野的全面发展的人才。

忽视任何一方，对数学的理解都是不完整的。因此，在数学教育中融入数学史，或在学习数学时主动了解其历史背景，是深化理解、提升兴趣、培养健全数学素养的关键途径。

数学史庞杂而悠久，却又深刻凝练，如果用一个轻松易读的短的篇幅讲清数学史呢？

日本著名数学家矢野健太郎就曾写过一本书，用短小的篇幅讲清楚了数学史的重要发展历程。从史前时代人类对数的认识起步，到逐渐形成五进制、十进制、二十进制等记数方法的过程，再到数学史上的重要转折点，如 0 的发现、方程的发展、对数的诞生，以及解析几何、微积分等重大突破。以及拓扑学、集合和概率论等不同领域的拓展。

因其平易近人，却又能以精简的篇幅，将纷繁交错的数学分支框架搭建起来，而广受赞誉。上市60余年，重印70多次，成为历久弥新的经典著作！

来源 | 《一口气读完的数学史：从手指计数到AI文明》

作者 | [日] 矢野健太郎

译者 | 逸宁

节选自 第 5 章　拓扑学

01

一笔画问题

拓扑的发源地

历史上的东普鲁士有座城市叫哥尼斯堡。在第二次世界大战期间，该城市曾被德军长期占据，直到1945 年 4 月 9 日被苏军攻克。根据 1945 年 7 月发布的《波茨坦公告》，该城市划归苏联。

为了纪念苏联革命家米哈伊尔·伊万诺维奇·加里宁（1875—1946），该城市由哥尼斯堡改名为加里宁格勒。

可以说，现在的加里宁格勒、过去的哥尼斯堡就是下面介绍的拓扑学的发源地。

哥尼斯堡七桥问题

如下图所示，普雷格尔河横贯哥尼斯堡这座城市，河上架有七座桥，分别被标记为 1、2、3、4、5、6、7。

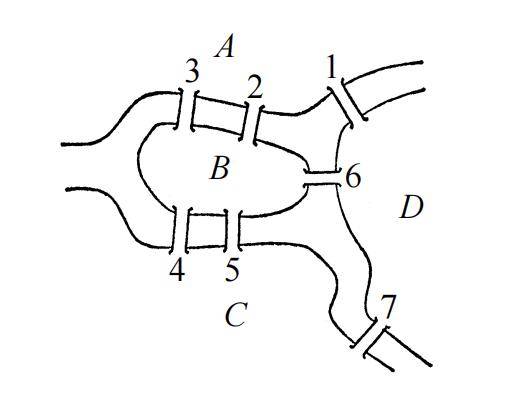
有一天，哥尼斯堡的一位市民提出了以下问题：

“一个步行者能否不重复、不遗漏地一次走完七座桥？”

其他市民认为该问题非常有趣，纷纷在地图上尝试了各种行走路线。

做不到且无法证明

若按照下图中虚线标出的路线行走，从 A 区出发，经过 1、6、2、3、4、7 这六座桥后到达 D 区，会遗漏5 号桥。如果想经过 5 号桥，就不得不再次经过 6 号桥或 7 号桥。

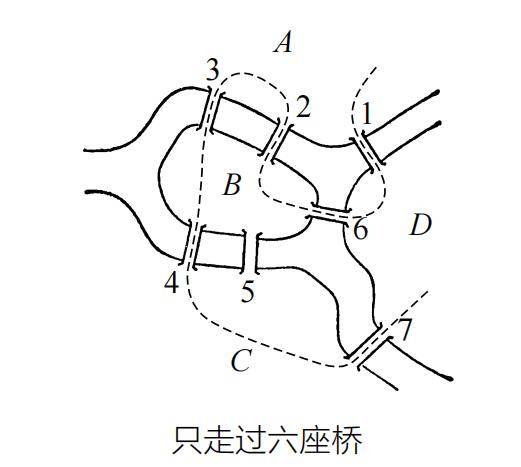
哥尼斯堡的市民绞尽脑汁研究这个问题，但谁也无法给出答案。因此，他们开始怀疑“不重复、不遗漏地一次走完七座桥”是不可能的，但是谁也证明不了这一点。

一笔画问题

当时的数学家欧拉（1707—1783）听说了此事，对于这个“不可能”给出了两种巧妙的证明方法。下面我将介绍其中一种方法，那就是把该问题转换成一笔画问题，从而证明其不可能。

首先，把被普雷格尔河分隔开的四部分区域分别命名为 A、B、C、D，然后把连接着这四部分区域的七座桥 1、2、3、4、5、6、7 和 A、B、C、D 用线连接起来，可以得到下图。

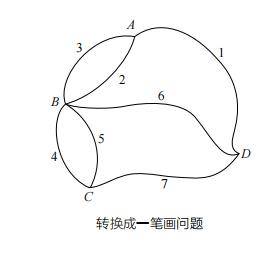
那么，“能否不重复、不遗漏地一次走完七座桥”的问题就变成了“能否一笔画出上面的图形”的问题，也就是所谓一笔画问题。

引出奇数条线的点 A

下面我们来研究可以一笔画出的图形。

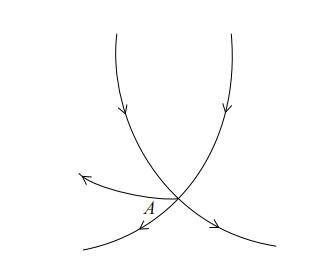
如上图所示，假设点 A 为一笔画的起点，而不是终点。那么，最初从 A 起笔时会从该点引出一条线。不过，在画图的过程中可能还会再次经过点 A，因为 A不是终点，所以只是经过而非终止。每经过一次点 A，就会增加两条从 A 引出的线。

因为 A 是起点，所以最初会引出一条线，后面每经过一次点 A 就增加两条线，那么最终从点 A 引出的线的数量为奇数。这种情况可以总结为：

（1）当一笔画的起点不是终点时，从起点引出的线的数量为奇数。

引出奇数条线的点 B

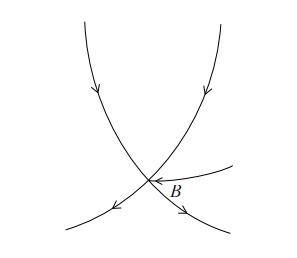
如上图所示，假设点 B 为一笔画的终点，而不是起点。那么，虽然点 B 不是起点，但在画图的过程中可能会经过点 B 多次。同样，每经过一次点 B，就会增加两条从 B 引出的线。此外，因为一笔画在点 B 结束，所以最后还会增加一条从 B 引出的线。

由于每经过一次点 B 就增加两条线，最后在点 B结束会再增加一条线，因此最终从点 B 引出的线的数量为奇数。也就是说：

（2）一笔画从非起点的终点引出的线的数量为奇数。

引出偶数条线的点 A（B）

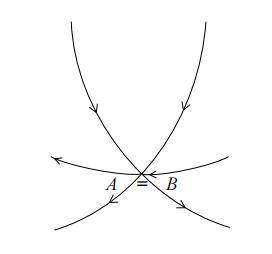
如上图所示，假设一笔画的起点同时也是终点。

在这种情况下，我们可以把前面提到的点 A 和点 B 视为同一点。因为该点为一笔画的起点，所以最初会从该点引出一条线。在后面画图的过程中可能会经过该点多次，每经过一次就会增加两条线。此外，因为一笔画会在该点结束，所以最后还会从该点引出一条线。

综上所述，起笔增加一条线，每经过一次增加两条线，收笔再增加一条线，那么最终从该点引出的线的数量为偶数。也就是说：

（3）当一笔画的起点和终点为同一点时，从该点引出的线的数量为偶数。

引出偶数条线的点 C

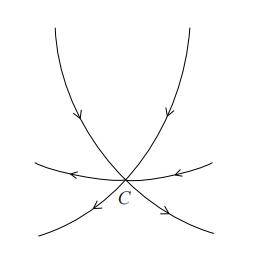
如上图所示，假设一笔画的点 C 既不是起点，也不是终点。在这种情况下，一笔画只是经过点 C。那么，无论经过点 C 多少次，每经过一次就会增加两条线。

那么最终从点 C 引出的线的数量为偶数。也就是说：

（4）一笔画从既不是起点也不是终点的点引出的线的数量为偶数。

一笔画定理及其应用

前文已经分析了所有情况，由此可以得出一个重要定理：一个图形要能一笔画成，必须满足引出奇数条线的点为起点或终点。

首先，让我们通过下页图所示的著名一笔画问题来了解该定理的应用。

平面内有六个点 A、B、C、D、E、F，其中从 A 和 B 引出的线有奇数条，从 C、D、E、F 引出的线有偶数条。那么，对于 A 和 B 而言，二者中的一点必须为起点，另一点必须为终点。只要记住这一点，得到一笔画的路径就不是难事了。

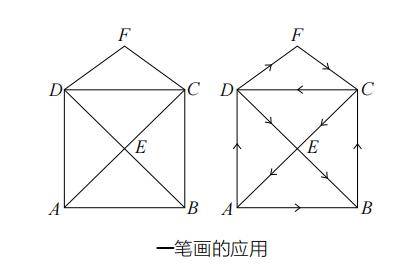
例如，从上面右侧图中的 A 点开始，在 B 点结束，便能得到一笔画的路径。

如果从 A、B 以外的点开始，则该图形绝对不能一笔画成。

若去掉“屋顶”则违背定理

那么，从这个著名的一笔画图形中去掉“屋顶”的部分，变成下面的图形后，能否一笔画成呢？

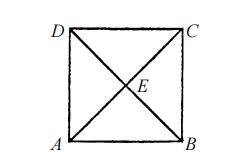
可以看到，在该图形中引出奇数条线的点为 A、B、 C、D 这四个点。那么，根据前面的定理可知，这四个点必须为起点或终点。然而，不可能有四个点都为起点或终点，所以该图形不能一笔画成。

欧拉对哥尼斯堡七桥问题的解答

基于以上定理，让我们重新思考哥尼斯堡七桥问题。这个问题可转换为下图所示的一笔画问题。

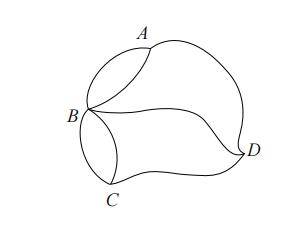
该图中有 A、B、C、D 四个点。从这些点引出的线的数量有 3 条或 5 条，也就是奇数条。那么，根据前面的定理可知，这四个点必须全部为起点或终点。

然而，这是不可能的，所以该图不能一笔画成。

因此，对于哥尼斯堡七桥问题，欧拉给出的结论是：一个步行者无法不重复、不遗漏地一次走完哥尼斯堡的七座桥。

02

拓扑学概览

即使发生形变，性质也保持不变

下面我们把前文提到的一笔画图形画到一张橡胶膜上，然后拉住 A、B、C、D、F 这五个角。

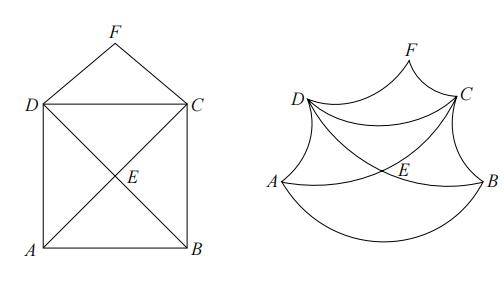
上图左侧的一笔画图形会发生上图右侧图形这种扭曲。但是，尽管图形发生了扭曲，一笔画成的性质依然保持不变。也就是说，形变后的图形依然能一笔画成。

因此，发生形变的橡胶膜具有以下性质：点发生移动时，最初相距较远的点在移动后依然相距较远。同样，最初相距较近的点在移动后依然相距较近。

拓扑变换与其条件

一般来说，当对一个图形施加某种操作，使其变为另一个图形时，如果满足以下条件，则称之为拓扑变换。

（1）这种变换是一一对应的。

也就是说，最初图形上的一点仅对应发生变换后的图形上的一点，变换后的图形上的一点仅对应最初图形上的一点。

（2）这种变换是连续的。

也就是说，在最初的图形上取两点 P 和 Q，若使点 Q 向点 P 无限靠近，则在变换后的图形上对应的点Q' 也会向点 P' 无限靠近。

反过来，若变换后的图形上的点Q' 向点 P' 无限靠近，则在与之对应的最初图形上相应的点 Q 会向点 P无限靠近。

如前文所述，一个图形能否一笔画成的性质在拓扑变换中保持不变。这种只着眼于在拓扑变换中保持不变的性质的几何学叫作拓扑学。

拓扑变换中保持不变的性质

下面举例说明拓扑变换中保持不变的性质。首先，想象平面内有一条连续且封闭的曲线。我们把这样的曲线称为简单闭曲线。

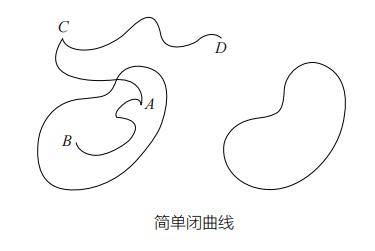
显然，简单闭曲线具有以下性质：“简单闭曲线把整个平面分为两部分，分别叫作内部和外部。”有边界的部分为内部，没有边界的部分为外部。

对于该简单闭曲线而言，位于其内部的两点 A 和 B 仍然在内部被某条连续曲线连接着，位于其外部的两点 C 和 D 仍然在外部被某条连续曲线连接着。不过，连接内部的点 A 和外部的点 C 的连续曲线一定与该简单闭曲线相交。

简单闭曲线的这种性质属于拓扑变换中保持不变的性质，由于若尔当（1838—1922）在其著作《分析教程》中首次提出这一理论，因此它被称为若尔当定理。

单连通区域和多连通区域

在平面内画出一个圆，然后在该圆的内部构想出一条简单闭曲线，这条闭曲线在圆的内部可以通过连续变形缩成一点。

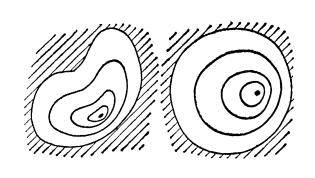
如前文所述，即使发生拓扑变换，这种性质也保持不变。

因此，当一区域内的简单闭曲线可以通过连续变形收缩成一点时，我们称该区域为单连通区域。

下面我们来思考夹在两个同心圆之间的区域。闭曲线在该区域内通过连续变形后不能缩成一点。因此，该区域不是单连通区域。

即使同心圆发生拓扑变换，这种性质也保持不变。一般来说，我们把这种非单连通区域叫作多连通区域。

双连通区域及三、四连通区域

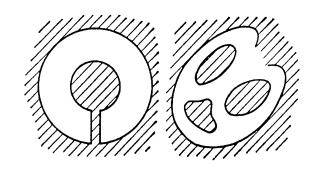
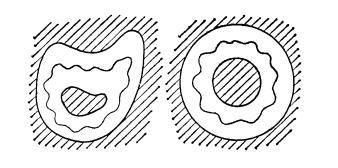
但是，如果把前面夹在同心圆之间的区域像上图左侧图形那样从边界到边界切割出一个开口，就能将其变成单连通区域。我们把这种区域叫作双连通区域。

同样，我们也可以定义三连通区域、四连通区域等多连通区域。上图右侧图形就是四连通区域的一个例子。

某区域为 n（正整数）连通区域的性质叫作拓扑性质。

球面、环面和简单闭曲线

下面来看立体图形的例子。

首先，我们尝试在一个球面上画出简单闭曲线。该闭曲线会把球面分成两部分。也就是说，若沿着这条闭曲线切割球面，球面会分成两部分。

然后，我们再来看看诸如甜甜圈、救生圈等环面。在环面上画的简单闭曲线未必能把环面分成两部分，如下图所示。也就是说，即使沿着这条简单闭曲线切割环面，也不能将其分成两部分。

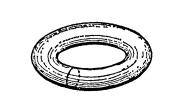
不过，如果再画出另一条简单闭曲线，就一定能把环面分成两部分，例如下图所示的简单闭曲线。

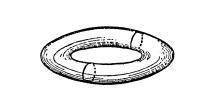
无法把甜甜圈一分为二的线数

可以说环面是有一个洞的曲面，下面我们来思考有两个洞的曲面。

当然，在有两个洞的曲面上画出的一条简单闭曲线无法把该曲面分成两部分。该曲面上画的两条简单闭曲线也不能将其分成两部分。

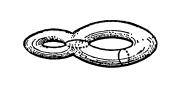
但是，若在该曲面上画出三条简单闭曲线，则一定能把该曲面分成两部分。

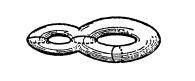
对于这种封闭的曲面，可以推导出无法把曲面分成两部分的简单闭曲线的数量。我们把这一数量叫作亏格。

正如前文所述，球面的亏格为 0，环面的亏格为 1，有两个洞的曲面的亏格为 2……一般来说，有 p 个洞的曲面的亏格为 p，而且即使发生拓扑变换，曲面的亏格也保持不变。

03

多面体

顶点数-边数+面数=2

前面已经讲过，毕达哥拉斯学派的学者证明了正多面体只有 5 种，分别是正四面体、正六面体、正八面体、正十二面体和正二十面体。

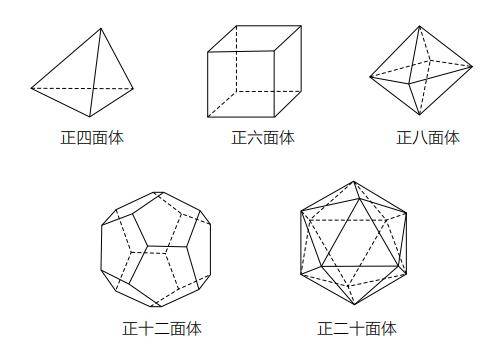
通过观察上图中各个正多面体的顶点数、边数和面数，统计后可得到下页的表。

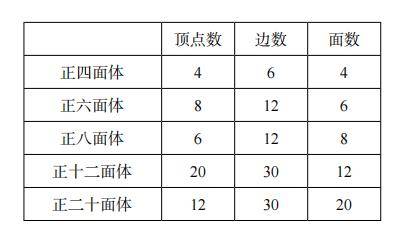
通过计算可以发现，顶点数减边数再加面数的结果均为 2。

这就是欧拉定理

若用 V 表示顶点数、E 表示边数、F 表示面数，则V-E+F=2 这个等式恒成立。解决一笔画问题的欧拉证明了“对于亏格为 0 的多面体，该等式恒成立”。例如下面这个多面体，顶点数为 8，边数为 14，面数为8，所以 8-14+8=2。这个事实叫作欧拉定理，下面我来介绍该定理的证明过程。

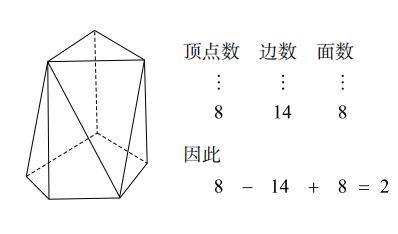
先去掉顶部的三角形

首先，去掉这个多面体的一个面，例如顶部的三角形。去掉这个面后，面数 F' 减少了 1，所以只要对下页中图（1）的多面体证明 V E F' 1 成立即可。

去掉一个面后，把剩下的表面变形、展开、平放到一平面上，由此可得到图（2），其中包含三角形、四边形和五边形。

然后，如图（3）中虚线所示，通过画对角线的方式把四边形和五边形分成三角形。

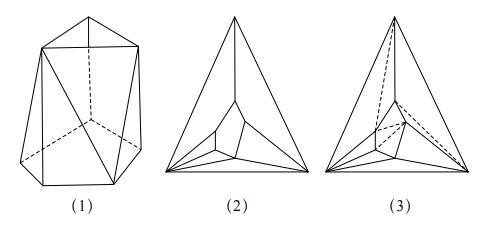
那么，每画一条对角线，顶点数 V 保持不变，边数E 增加 1，面数 F' 也增加 1，所以需要证明的等式的数值保持不变。

去掉最外侧的边

接下来去掉图（4）最外侧的一条边。那么顶点数V 保持不变，边数 E 减少 1，面数 F' 减少 1，所以需要证明的等式的数值依旧保持不变。

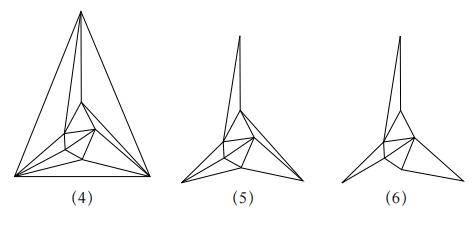
反复执行三次这种操作后便能得到图（5），如果进一步去掉该图外侧三角形的一边，就能得到图（6）。

去掉最外侧的顶点

然后，去掉最外侧三角形的一个顶点以及相交于该顶点的两边。此时顶点数 V 减少 1，边数 E 减少 2，面数 F' 减少 1，所以需要证明的等式的数值保持不变。

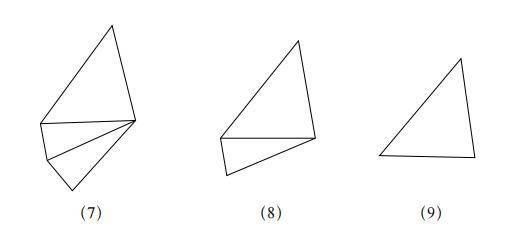
如果对图（6）执行三次这种操作，就会得到上图中的图（7），如果继续去掉最外侧三角形的一个顶点以及相交于该顶点的两边，就会依次得到图（8）、图（9）。而且，如前文所述，经过以上一系列操作后，需要证明的等式的数值保持不变。

证明完毕

于是，最后只剩一个三角形。对于该三角形而言，顶点数 V 为 3，边数 E 为 3，面数 F' 为 1，所以需要证明的等式的数值为 1，即 V -E +F' 1。由 F'= F- 1可知，V- E +F =2。综上所述，欧拉定理的证明就此结束。

对于亏格为 p 的多面体，欧拉还证明了以下等式成立。

该等式的右侧叫作多面体的欧拉示性数。多面体的亏格和欧拉示性数在拓扑变换中都保持不变。