2025年学生将迎来新版教材，新教材将更加重视思维和阅读！为了方便广大学生在暑假预习新学期的课本知识，我们整理了2025新西南大学版六年数学（上册）一电子课本，以图片的形式呈现给大家，希望对同学们的暑期学习有所帮助。

以下是部分内容截图，完整信息请查看 PDF 文件

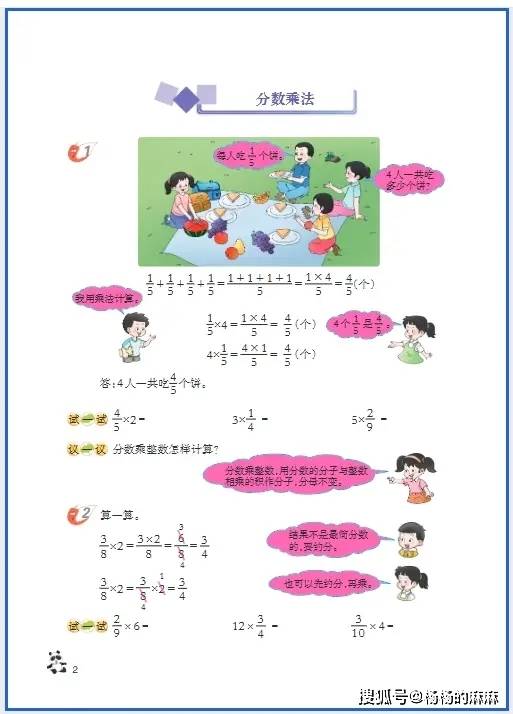
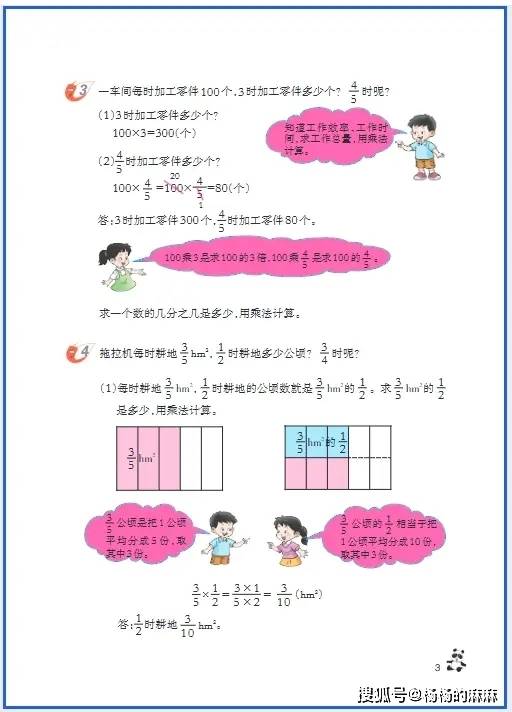
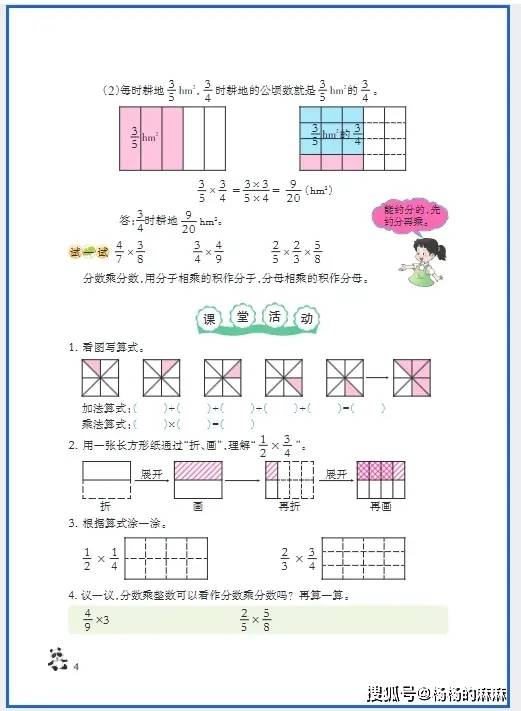
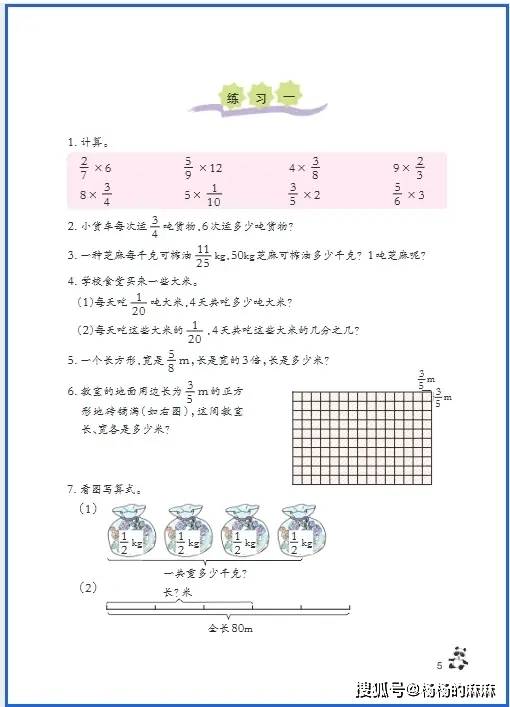
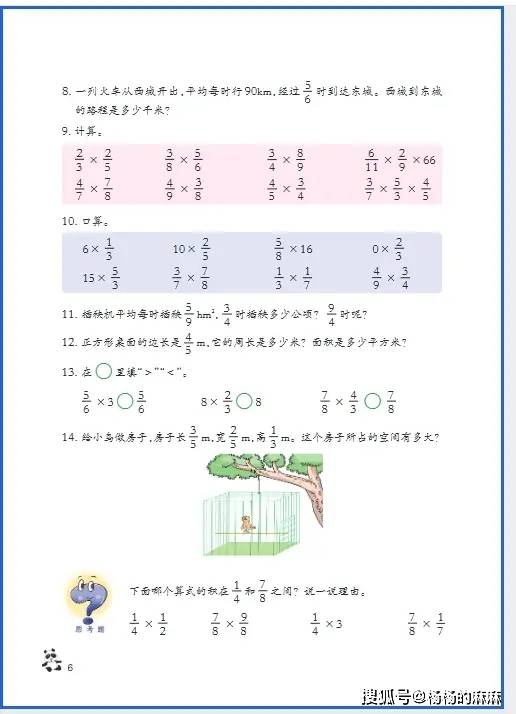
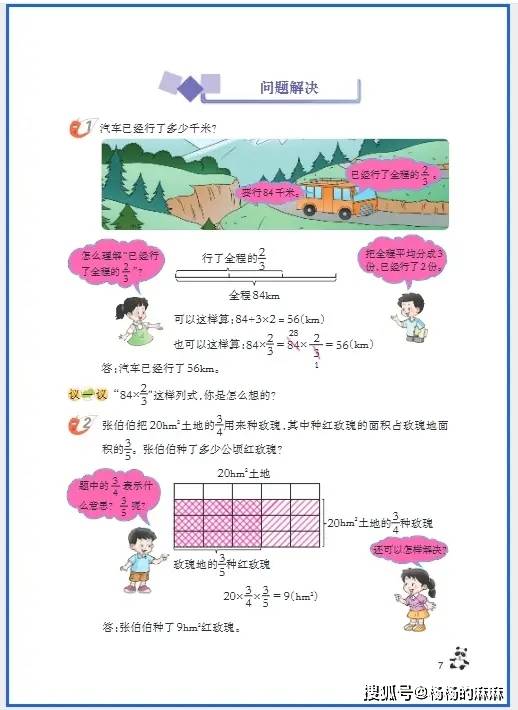
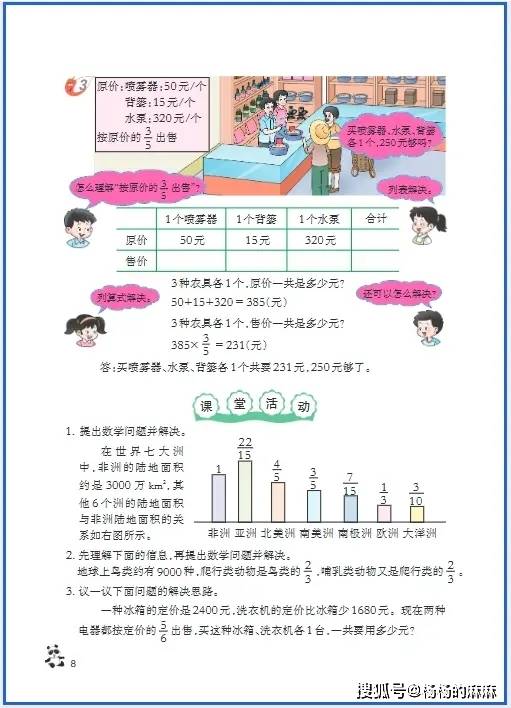
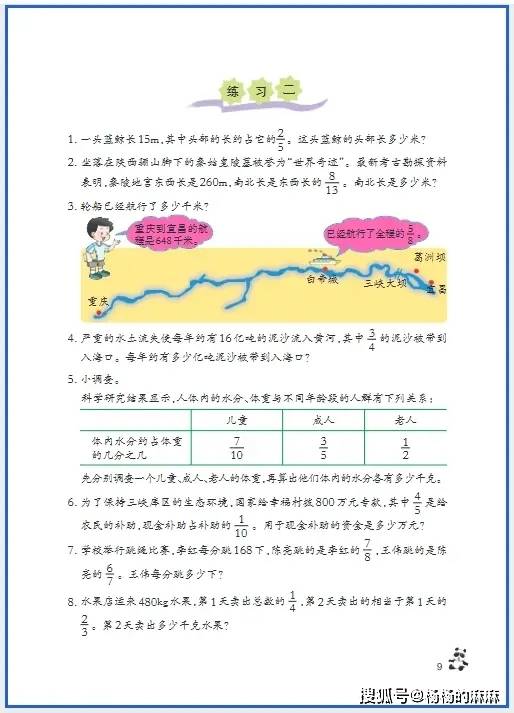
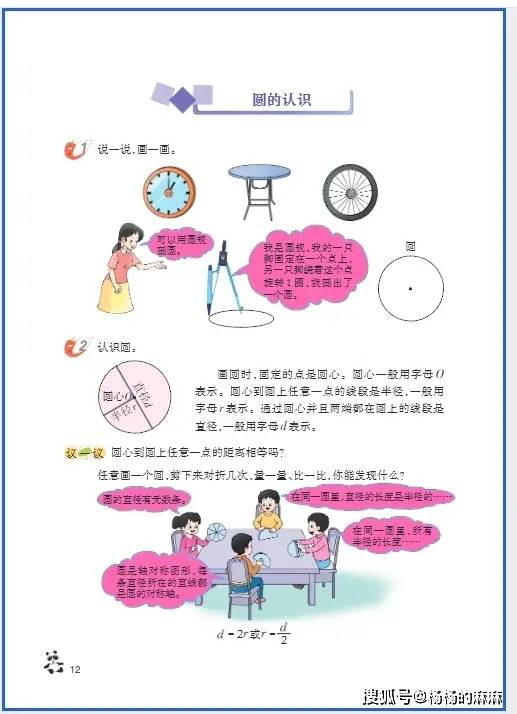
六年级是小学数学知识体系的 “收官阶段”，既要整合整数、小数、分数的运算逻辑，又要攻克立体几何（圆柱与圆锥）、比与比例等抽象内容，同时需培养 “综合运用知识解决复杂问题” 的能力，为初中数学衔接奠定基础。以下从基础巩固、思维进阶、习惯养成三大维度，提供针对性学习方法：

一、夯实基础：打通 “知识关联”，拒绝 “碎片化记忆”

六年级数学的核心是 “知识串联”，如分数、百分数、比之间的转化，圆柱与圆的公式关联，需做到 “理解逻辑、灵活调用”，而非孤立记忆。

1. 吃透 “知识本质”，用 “关联法” 理解抽象概念

六年级难点（如负数、正比例 / 反比例、立体图形体积）需结合已有知识搭建逻辑链，通过 “生活场景 + 旧知迁移” 突破抽象壁垒：

• 学 “负数” 时：结合 “温度计刻度”（零上 5℃记为 + 5℃，零下 3℃记为 - 3℃）、“电梯楼层”（地面以上 3 层记为 + 3，地下 1 层记为 - 1），理解 “正负数表示相反意义的量”，同时关联 “数轴”（明确 - 2＜0＜1 的大小关系）；
• 学 “圆柱体积” 时：先回顾 “长方体体积 = 底面积 × 高”，再通过 “切割圆柱拼成长方体” 的实验，发现 “圆柱底面积 = 长方体底面积，圆柱高 = 长方体高”，推导圆柱体积公式
• V=Sh
• ，并关联 “圆的面积公式”（
• S=πr2
• ），形成 “圆→圆柱→长方体” 的知识链；
• 学 “比与百分数” 时：用 “果汁配比” 实例（1 份果汁配 4 份水，果汁与水的比是 1:4，果汁占总量的 20%），理解 “比、分数、百分数的互通性”（1:4=
• 5
• 1
• =20%），避免概念混淆。

2. 强化 “计算能力”，做到 “精准 + 灵活”

六年级计算涵盖 “分数四则混合运算”“百分数与小数互化”“比例计算”，需兼顾正确率与方法优化：

• 每日 15 分钟 “分层计算练习”：基础层练 “分数乘除（如
• 4
• 3
• ×9
• 8
• ）”“百分数化简（如 60%:
• 5
• 3
• ）”；提升层练 “混合运算（如
• 3
• 2
• ×(6
• 5
• −4
• 1
• )÷8
• 7
• ）”“解比例（如
• 2.4
• x
• =8
• 5
• ）”，针对性突破 “通分失误”“比例内项外项混淆” 等问题；
• 建立 “计算错题档案”：按 “错误类型” 分类记录（如 “分数除法忘乘倒数”“π 取值错误导致圆面积算错”“解比例时漏写单位”），每周用 “错题重做 + 同类题拓展” 巩固，避免重复出错；
• 善用 “简便算法” 提效：熟记运算律（如乘法分配律在分数中的应用：
• 7
• 5
• ×4
• 3
• +7
• 5
• ×4
• 1
• =7
• 5
• ×(4
• 3
• +4
• 1
• )
• ），灵活转化形式（如计算 “圆柱侧面积” 时，若已知直径和高，可直接用
• S=πdh
• ，无需先算半径）。

二、培养思维：从 “单一解题” 到 “综合应用”

六年级数学强调 “逻辑推理” 与 “知识整合”，如用比例解行程问题、结合圆柱体积与百分数算实际用量，需建立 “多维度分析问题” 的思维模式。

1. 用 “流程化思维” 解复杂应用题，拒绝 “盲目列式”

六年级应用题（如 “税率利率问题”“立体图形体积实际应用”“比例行程问题”）条件多、关联强，可按 “四步拆解法” 突破：

• 第一步：“梳理条件关系”：用表格或线段图整理信息（如 “本金 10000 元，年利率 2.75%，存 3 年，求利息”，可列出 “本金 = 10000 元，利率 = 2.75%，存期 = 3 年，求利息”）；
• 第二步：“确定解题模型”：对应知识点选择公式（如 “利息 = 本金 × 利率 × 存期”“圆锥体积 =
• 3
• 1
• πr2
• h
• ”），明确 “单位是否统一”（如 “圆柱高是 2 分米，半径是 5 厘米，需先统一为厘米或分米”）；
• 第三步：“分步列式计算”：按逻辑分步书写（如 “一个圆锥形沙堆，底面半径 2 米，高 1.5 米，每立方米沙重 1.8 吨，求沙堆总重”，先算体积：
• 3
• 1
• ×3.14×22
• ×1.5=6.28
• 立方米，再算总重：
• 6.28×1.8=11.304
• 吨）；
• 第四步：“验证结果合理性”：结合生活实际判断（如 “计算商品折扣时，八折后的价格应比原价低”“圆锥体积应比等底等高的圆柱体积小”），避免明显错误。

2. 用 “跨模块解题” 拓展思维，打破 “知识壁垒”

六年级知识关联性强，同一问题可结合不同模块解法，培养 “综合调用能力”：

• 求 “环形面积”：既可用 “大圆面积 - 小圆面积”（
• πR2
• −πr2
• ），也可结合 “比的知识”（若大圆与小圆半径比是 3:2，面积比是 9:4，用总量差对应份数差计算）；
• 解 “行程问题”：如 “甲、乙两车从两地相向而行，速度比是 3:2，相遇时甲走了 180 千米，求两地距离”，既可用 “比例法”（路程比 = 速度比 = 3:2，乙走 120 千米，总距离 300 千米），也可用 “分数法”（甲走全程的
• 5
• 3
• ，全程 = 180÷
• 5
• 3
• =300 千米），还可设未知数用 “方程法” 求解；
• 分析 “扇形统计图”：如 “某班扇形图中，喜欢足球的占 25%，喜欢篮球的占 30%，喜欢足球的比篮球少 5 人”，既可用 “百分数差求总量”（5÷(30%-25%)=100 人），也可通过 “比的关系”（足球：篮球 = 5:6，份数差 1 对应 5 人，总人数 11×5=55？不，此处需纠正，应先算总量：5÷5%=100，再按比例分配），对比不同方法的适用场景，提升思维灵活性。

三、习惯养成：从 “被动学习” 到 “主动规划”

六年级需培养 “自主梳理知识”“规范解题”“考前复习” 的习惯，为初中自主学习打基础。

1. 建立 “知识思维导图”，定期梳理体系

每学完一个单元（如 “圆柱与圆锥”“比例”），用思维导图整理 “核心知识点 + 公式 + 易错点”：

• 以 “圆柱与圆锥” 为例：中心主题下分 “特征”“表面积”“体积”“应用” 分支，“表面积” 下再分 “侧面积公式（
• S=Ch
• ）”“完整表面积（
• 2πrh+2πr2
• ）”“无盖 / 无底情况（如水桶表面积 = 侧面积 + 1 个底面积）”，标注易错点 “单位统一”“π 的取值（题目未说明时取 3.14）”；
• 期末前整合 “全册知识网”：将 “数与代数”（分数、百分数、比、比例）、“图形与几何”（圆、圆柱、圆锥）、“统计与概率”（扇形统计图）串联，明确 “分数除法→比→比例”“圆的面积→圆柱底面积→圆柱体积” 的推导关系，避免知识碎片化。

2. 规范 “解题格式”，养成严谨习惯

六年级解题需注重 “步骤完整、书写清晰”，尤其是几何题和应用题：

• 几何题：如 “求圆锥体积”，需先写 “已知条件”（底面半径 r=3cm，高 h=5cm），再写 “公式”（
• V=3
• 1
• πr2
• h
• ），代入数值时带单位（
• V=3
• 1
• ×3.14×32
• ×5
• ），计算过程分步写（
• =3
• 1
• ×3.14×9×5=47.1
• cm³），最后写 “答句”；
• 应用题：避免 “跳步”，如 “某商品原价 200 元，先涨价 10%，再降价 10%，求现价”，需分步算 “涨价后价格：200×(1+10%)=220 元”“降价后价格：220×(1-10%)=198 元”，明确每一步的逻辑，便于检查纠错。

3. 考前 “针对性复习”，高效查漏补缺

期末复习时，按 “三步法” 提升效率：

• 第一步：“错题重做”：重点复习 “错题档案” 和 “作业错题”，尤其是 “反复出错的类型”（如 “正比例反比例判断错误”“圆锥体积忘乘
• 3
• 1
• ”）；
• 第二步：“专项突破”：针对薄弱模块（如 “立体图形表面积计算”“比例应用题”），集中做 10-15 道同类题，总结解题规律；
• 第三步：“模拟演练”：用期末真题模拟考试，计时完成，训练 “时间分配能力”（如 “计算类题控制在 20 分钟内，应用题每道题不超过 5 分钟”），同时检查 “单位是否遗漏”“答句是否完整” 等细节问题。