2025年学生将迎来新版教材，新教材将更加重视思维和阅读！为了方便广大学生在暑假预习新学期的课本知识，我们整理了2025新人教版八年级数学（上册）一电子课本，以图片的形式呈现给大家，希望对同学们的暑期学习有所帮助。

以下是部分内容截图，完整信息请查看 PDF 文件

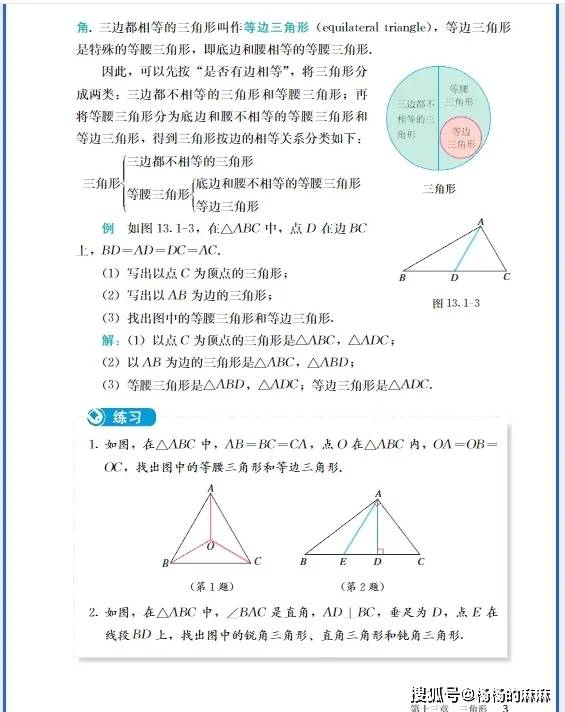
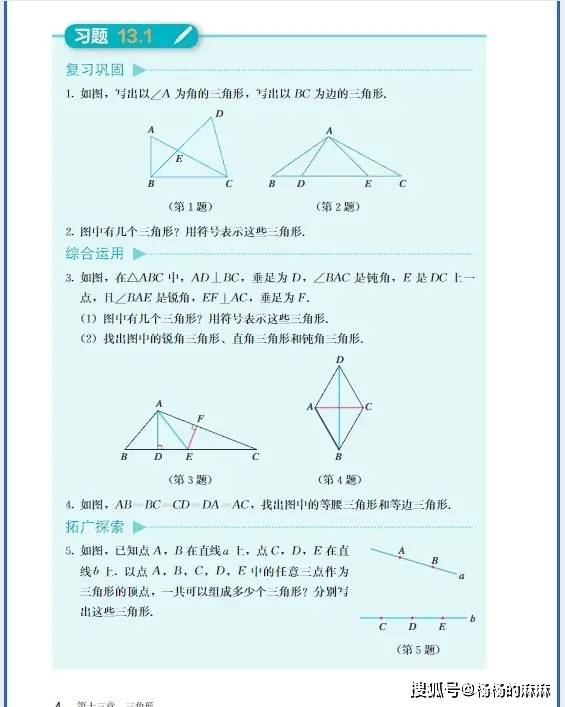
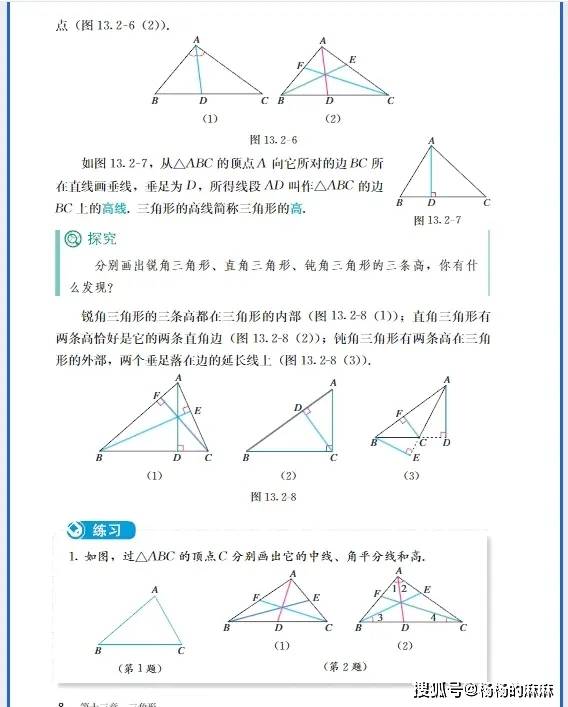
八年级数学是初中阶段的 “知识深化与能力转型期”，既要巩固初一有理数、方程等基础，又要学习 “几何推理”“函数初步”“复杂方程” 等新内容，核心是 “建立逻辑思维、掌握解题方法、应对综合题型”。以下按教材高频模块拆解核心知识，附常考题型与学习重点，帮你系统把握八年级数学脉络：

一、八年级数学核心知识模块（贴合教材高频内容）

1. 全等三角形（几何推理入门，八年级上册重点）

作为初中几何的 “推理基础”，全等三角形核心是 “通过边、角关系证明图形全等，进而解决线段、角相等问题”，不再是初一简单的图形识别。

• 核心内容：
• 全等三角形的性质：对应边相等、对应角相等（如△ABC≌△DEF，则 AB=DE，∠A=∠D）；
• 全等三角形的判定定理：SSS（三边对应相等）、SAS（两边及其夹角对应相等）、ASA（两角及其夹边对应相等）、AAS（两角及其中一角的对边对应相等）、HL（直角三角形专用：斜边和一条直角边对应相等）；
• 角平分线的性质与判定：性质（角平分线上的点到角两边的距离相等）、判定（到角两边距离相等的点在角的平分线上），常结合全等三角形证明。
• 常考题型：
• 基础证明：“已知 AB=CD，∠A=∠C，求证△ABC≌△CDA”（用 SAS 或 ASA 判定）；
• 综合应用：“已知 AD 是∠BAC 的平分线，BD⊥AB，DC⊥AC，求证 BD=DC”（用角平分线性质 + 全等证明）；
• 辅助线添加：如 “遇中点连中线”“遇角平分线作垂线”，构造全等三角形（如已知 AB=AC，AD 是中线，连 AD 证明△ABD≌△ACD）。

2. 轴对称（几何图形性质拓展，衔接等腰三角形）

围绕 “图形对称特性” 展开，核心是 “利用轴对称性质解决线段最短、角度计算问题”，并结合等腰三角形深化应用。

• 核心内容：
• 轴对称的性质：对称轴是对应点连线的垂直平分线；对应线段相等、对应角相等（如点 A 关于直线 l 的对称点是 A'，则 l⊥AA' 且 l 平分 AA'）；
• 等腰三角形的性质与判定：性质（两腰相等、两底角相等，“三线合一”—— 顶角平分线、底边上的中线、底边上的高重合）；判定（等角对等边，即若∠B=∠C，则 AB=AC）；
• 最短路径问题：利用轴对称转化线段（如 “将军饮马” 问题：求直线 l 上一点 P，使 PA+PB 最短，作 A 关于 l 的对称点 A'，连接 A'B 与 l 的交点即为 P）。
• 常考题型：
• 等腰三角形计算：“已知等腰三角形顶角为 80°，求底角”（(180°-80°)/2=50°）；
• 轴对称应用：“已知点 A (2,3)，求其关于 x 轴的对称点坐标”（(2,-3)）；
• 最短路径作图与计算：“在河边 l 上建水泵站，向 A、B 两村供水，求最短管线长度”（用轴对称转化后计算）。

3. 一次函数（函数入门，八年级下册核心，衔接代数与几何）

作为初中第一个系统学习的函数，核心是 “理解变量关系、掌握图像性质、解决实际应用问题”，是后续学习反比例函数、二次函数的基础。

• 核心内容：
• 函数的概念：在一个变化过程中，有两个变量 x 和 y，对于 x 的每一个确定值，y 都有唯一确定值与之对应，则 y 是 x 的函数（如 y=2x+1）；
• 一次函数的形式与性质：形如 y=kx+b（k≠0），k 是斜率（决定函数图像倾斜方向：k>0 时 y 随 x 增大而增大，k<0 时 y 随 x 增大而减小），b 是截距（图像与 y 轴交点的纵坐标，即 (0,b)）；
• 一次函数与方程、不等式的关系：一次函数 y=kx+b 的图像与 x 轴交点的横坐标是方程 kx+b=0 的解；当 y>0 时，x 的取值范围是不等式 kx+b>0 的解。
• 常考题型：
• 一次函数性质应用：“已知一次函数 y=-2x+3，判断 y 随 x 的变化趋势，并求与 y 轴交点坐标”（y 随 x 增大而减小，交点 (0,3)）；
• 图像分析：“给出一次函数图像，求 k、b 的符号，或比较两点函数值大小”（如图像过一、二、四象限，则 k<0，b>0）；
• 实际应用：“某商店销售商品，成本 30 元 / 件，售价 x 元 / 件，销量 y= -2x+100，求利润 w 与 x 的函数关系”（w=(x-30)(-2x+100)= -2x²+160x-3000）。

4. 二元一次方程组（方程拓展，解决多变量问题）

在一元一次方程基础上升级，核心是 “消元转化为一元一次方程，解决含两个未知数的实际问题”，常与几何、函数结合出题。

• 核心内容：
• 二元一次方程组的概念：含有两个未知数，且含未知数的项的次数都是 1 的整式方程组（如
• {x+y=5
• 2x−y=1
• ）；
• 解法：代入消元法（把一个方程的一个未知数用含另一个未知数的式子表示，代入另一个方程）、加减消元法（把两个方程的某一未知数系数化为相反或相同，相加或相减消去该未知数）；
• 实际应用：常见类型有 “行程问题（两个物体运动）”“工程问题（两个工程队）”“配套问题（两种零件配套）”“利润问题（两种商品销售）”，关键是 “设两个未知数，找两个等量关系”。
• 常考题型：
• 解方程组：用代入法或加减法解
• {3x+2y=8
• x−y=1
• （解得 x=2，y=1）；
• 实际应用：“甲、乙两人从相距 20km 的两地相向而行，2 小时后相遇，甲比乙每小时多走 1km，求两人速度”（设甲速度 x km/h，乙 y km/h，列
• {x−y=1
• 2(x+y)=20
• ）。

5. 数据的分析（统计深化，从 “描述” 到 “分析”）

在初一数据收集的基础上，增加 “数据波动程度” 的分析，核心是 “用统计量（平均数、中位数、众数、方差）描述数据特征，做出决策”。

• 核心内容：
• 集中趋势统计量：平均数（加权平均数，如 “一组数据 3,5,5,7，加权平均数为 (3×1+5×2+7×1)/4=5”）、中位数（将数据从小到大排列后中间的数，或中间两数的平均数）、众数（出现次数最多的数）；
• 离散程度统计量：方差（衡量数据波动大小，方差越小，数据越稳定，公式：
• s2
• =n
• 1
• [(x1
• −x
• ˉ
• )2
• +(x2
• −x
• ˉ
• )2
• +…+(xn
• −x
• ˉ
• )2
• ]
• ）；
• 统计应用：根据统计量选择合适的方案（如 “选择参赛选手，看平均数；避免极端值，看中位数；选最普遍情况，看众数”）。
• 常考题型：
• 统计量计算：“已知一组数据 2,3,4,5,5，求中位数、众数、方差”（中位数 4，众数 5，方差 1.2）；
• 统计决策：“两家公司的工资数据，用平均数和方差分析哪家公司待遇更稳定”（方差小的公司待遇更稳定）。

二、八年级数学常见难点及突破方法

难点 1：全等三角形证明（辅助线添加、判定定理选择）

• 突破方法：
• 先 “找已知条件”：在图中标出已知的边、角（如 “AB=CD”“∠A=∠D”），判断已有条件符合哪个判定定理（如已有两边，缺夹角则用 SAS，缺第三边则用 SSS）；
• 记 “常见辅助线模型”：遇 “中点” 连中线（构造全等三角形）、遇 “角平分线” 作两边垂线（用角平分线性质）、遇 “线段和差” 截长补短（如证明 AB=CD+EF，在 AB 上截取 AG=CD，再证 GB=EF）；
• 多练 “基础证明题”，总结 “定理应用场景”（如 HL 只用于直角三角形，ASA 和 AAS 的区别在于 “夹边” 还是 “对边”）。

难点 2：一次函数图像与性质（数形结合理解）

• 突破方法：
• 从 “具体到抽象”：先画简单一次函数的图像（如 y=2x、y=-x+3），观察 k、b 变化时图像的变化（如 k 从 1 变 2，图像更陡；b 从 3 变 - 1，图像向下平移 4 个单位），理解 “数” 与 “形” 的对应关系；
• 用 “口诀记性质”：“k 正左低右高，y 随 x 增而增；k 负左高右低，y 随 x 增而减；b 正交 y 轴上，b 负交 y 轴下”；
• 结合 “方程、不等式” 练综合题：如 “已知一次函数 y=kx+b 过 (1,2)、(2,0)，求不等式 kx+b>0 的解”（先求函数解析式 y=-2x+4，再解 - 2x+4>0，得 x<2）。

难点 3：二元一次方程组应用题（找等量关系）

• 突破方法：
• 读题时 “圈关键词”：如 “相向而行”“相遇”“总工作量”“配套比例”，明确两个未知数（如 “甲的速度” 和 “乙的速度”，“生产桌面的数量” 和 “生产桌腿的数量”）；
• 用 “文字等式” 列等量关系：如 “甲走的路程 + 乙走的路程 = 总距离”“桌腿数量 = 4× 桌面数量”，再将文字转化为含未知数的等式；
• 分类练 “典型题型”（行程、工程、配套），总结 “等量关系模板”（如工程问题：“甲的工作量 + 乙的工作量 = 总工作量”）。

三、八年级数学学习方法（高效提分）

1. 重视 “逻辑推理”，不只会 “算” 还要会 “证”

八年级几何（全等三角形、轴对称）不再是初一 “算角度、算长度”，而是 “用定理证明结论”。学新课时，先搞懂 “定理的推导过程”（如为什么 SSS 能判定全等），再练 “证明步骤书写”—— 每一步都要写 “依据”（如 “∵AB=CD（已知），∠A=∠C（已知），AD=DA（公共边），∴△ABC≌△CDA（SAS）”），避免 “跳步” 导致逻辑漏洞。

2. 错题本 “分类整理”，针对性突破

按 “模块 + 错因” 分类记录错题：

• 几何证明题：记 “辅助线添加错误”“定理用错”，如 “误用 SSA 判定全等（SSA 不能判定）”，标注 “正确判定定理：SAS”；
• 函数题：记 “数形结合不熟练”，如 “不会根据图像求 k、b”，补充 “图像与坐标的关系：与 x 轴交点 (x,0)，与 y 轴交点 (0,b)”；
• 应用题：记 “等量关系找错”，如 “配套问题中桌腿数量算成‘桌面数量 = 4× 桌腿数量’”，重写 “正确等量关系：桌腿数量 = 4× 桌面数量”。每周花 30 分钟复习错题，避免重复犯错。

3. 练 “综合题”，培养 “知识串联” 能力

八年级考试常考 “跨模块综合题”（如 “一次函数与二元一次方程组结合”“全等三角形与轴对称结合”）。平时练习时，有意识地找这类题目：

• 如 “已知一次函数 y=kx+b 的图像过 A (1,3)、B (2,5)，求△AOB 的面积（O 为原点）”（先求函数解析式，再找与坐标轴交点，用面积公式计算）；
• 练完后总结 “串联点”（如 “函数图像上的点坐标满足函数解析式，可用于求线段长度”），提升综合解题能力。

4. 用 “生活实例” 理解抽象知识

面对函数、几何等抽象内容，结合生活场景理解：

• 学一次函数时，把 “y=2x+3” 看作 “买文具，每支笔 2 元，外加 3 元运费，总费用 y 与笔的数量 x 的关系”；
• 学轴对称时，观察 “蝴蝶翅膀”“窗户图案”，理解 “对称的特性”。用 “具体实例” 降低抽象难度，后续应用会更灵活。

八年级数学是初中学习的 “分水岭”，既要扎实掌握 “全等三角形、一次函数、二元一次方程组” 等核心模块，又要培养 “逻辑推理、数形结合” 的思维能力。只要按 “理解概念→练基础题→攻综合题→总结错题” 的步骤坚持，就能轻松应对八年级数学的进阶挑战，为九年级冲刺中考打下坚实基础！