北师大版八年级语文人教版八年级数学（上下册）电子课本可以方便大家随时随地预习或复习课本知识，为此，我们找到了北师大版八年级数学（上下册）新教材电子书教材的全部内容，以高清图片的形式呈现给大家，希望能够提高大家的学习效率。

如需全套电子课本PDF版，请关注公众号“桃李百科”回复：“电子课本”

北师大版八年级数学（上下册）新教材电子课本在线阅读（此为截图版，获取是高清版）

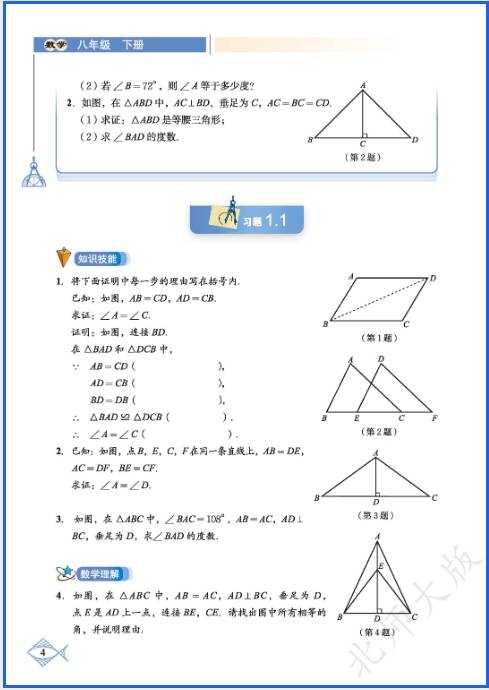
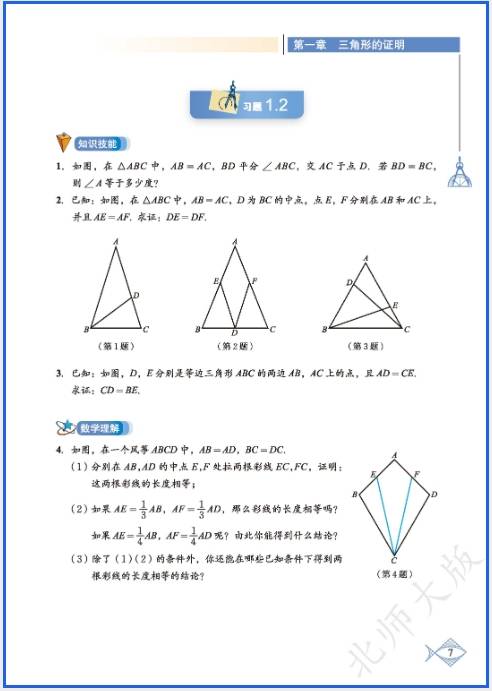
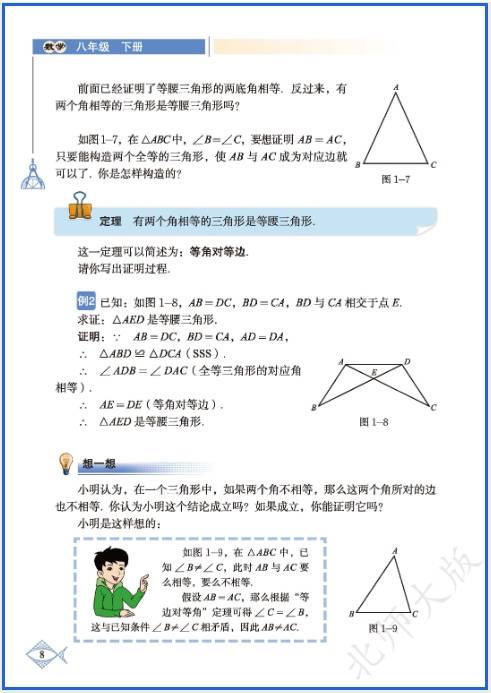
八年级上册

• 分式
• 分式的概念与性质：具备\(\frac{A}{B}\)形式（\(A\)、\(B\)为整式，\(B\)含字母且\(B\neq0\)）的式子即分式；其基本性质为分子分母同乘（或除以）非零整式，分式值不变。
• 分式的运算：涵盖乘除、加减运算，混合运算时需遵循运算顺序。
• 分式方程：分母含未知数的方程，求解关键在于去分母化为整式方程，要注意检验增根，使分母为\(0\)的根即为增根。
• 实数与二次根式
• 实数的分类：有理数和无理数共同构成实数。
• 二次根式的概念：形如\(\sqrt{a}\)（\(a\geq0\)）的式子为二次根式。
• 二次根式的性质：\((\sqrt{a})^{2}=a\)（\(a\geq0\)），\(\sqrt{a^{2}}=\vert a\vert\) 。
• 二次根式的运算：乘法运算为\(\sqrt{a}\cdot\sqrt{b}=\sqrt{ab}\)（\(a\geq0\)，\(b\geq0\)），除法运算为\(\frac{\sqrt{a}}{\sqrt{b}}=\sqrt{\frac{a}{b}}\)（\(a\geq0\)，\(b>0\)），加减法需先将二次根式化为最简形式，再合并被开方数相同的二次根式。
• 三角形
• 三角形的性质：三边存在任意两边之和大于第三边，任意两边之差小于第三边的关系；内角和为\(180^{\circ}\)；三角形具有稳定性。
• 三角形的重要线段：包括高、中线、角平分线，要掌握它们各自的定义与性质 。
• 全等三角形：全等三角形的判定方法有 SSS、SAS、ASA、AAS、HL，性质是对应边相等、对应角相等。
• 等腰三角形与直角三角形：等腰三角形具备两腰相等、两底角相等以及三线合一的性质，判定方法是等角对等边；直角三角形有勾股定理等重要性质。
• 尺规作图与轴对称：掌握用尺规作角平分线、垂直平分线等操作；理解轴对称图形与轴对称的概念、性质，能够运用轴对称知识解决最短路径问题。
• 事件与可能性
• 确定事件和随机事件：明确必然事件、不可能事件和随机事件的概念 。
• 可能性的大小：借助概率来衡量事件发生可能性的大小。

八年级下册

• 一次函数
• 函数的概念：在某个变化过程中，存在两个变量\(x\)和\(y\)，给定一个\(x\)值能确定唯一的\(y\)值，此时称\(y\)是\(x\)的函数。
• 一次函数的表达式：\(y = kx + b\)（\(k\)，\(b\)为常数，\(k\neq0\)），当\(b = 0\)时，\(y = kx\)（\(k\neq0\)）为正比例函数。
• 一次函数的图象与性质：一次函数图象是一条直线，当\(k>0\)时，\(y\)随\(x\)增大而增大，图象从左到右上升；当\(k<0\)时，\(y\)随\(x\)增大而减小，图象从左到右下降。
• 一次函数的应用：能够构建一次函数模型解决实际问题。
• 四边形
• 平行四边形：了解平行四边形的定义，掌握其对边平行且相等、对角相等、对角线互相平分的性质，以及通过两组对边分别平行、两组对边分别相等、一组对边平行且相等、两组对角分别相等、对角线互相平分来判定平行四边形的方法。
• 特殊的平行四边形：矩形是有一个角为直角的平行四边形，具有四个角都是直角、对角线相等的性质；菱形是有一组邻边相等的平行四边形，四条边都相等，对角线互相垂直平分且每一条对角线平分一组对角；正方形兼具矩形和菱形的所有性质 。掌握矩形、菱形、正方形的判定方法。
• 梯形：掌握梯形的概念，等腰梯形具有两腰相等、同一底上的两个角相等、对角线相等的性质以及相关判定方法。