2025年学生将迎来新版教材，新教材将更加重视思维和阅读！为了方便广大学生在暑假预习新学期的课本知识，我们整理了2025新西南大学版四年级数学（上册）一电子课本，以图片的形式呈现给大家，希望对同学们的暑期学习有所帮助。

以下是部分内容截图，完整信息请查看 PDF 文件

四年级数学的核心重点，本质是完成 “具象运算” 到 “抽象思维” 的关键过渡，同时为后续学习筑牢基础知识点。这一阶段的内容可浓缩为四大核心模块，每个模块都承载着明确的能力培养目标与关键学习任务：

一、数与代数：运算能力的 “进阶突破期”

作为四年级数学的核心支柱，数与代数模块直接决定学生计算能力的 “上限”，核心目标是从 “会算” 升级为 “懂算、算快、算准”。

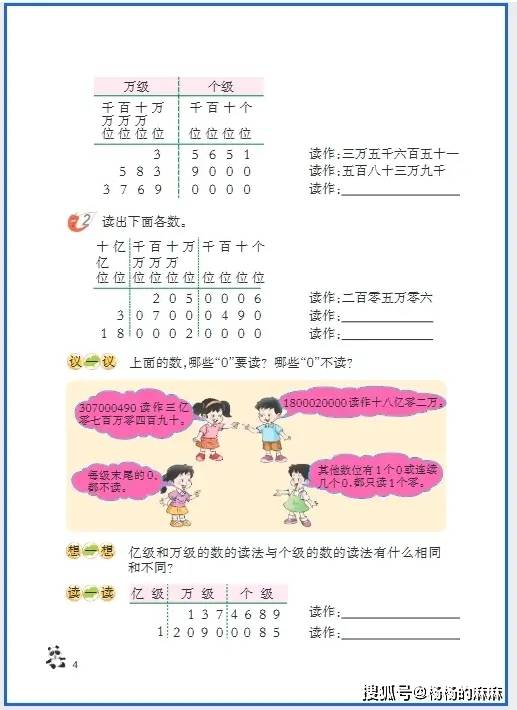
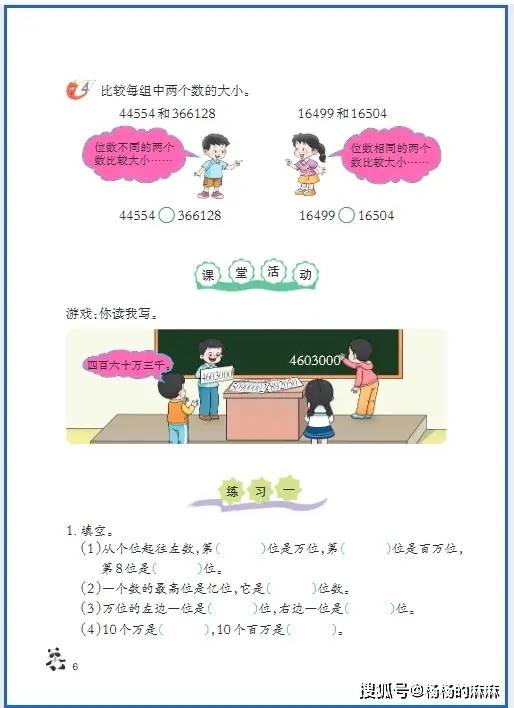
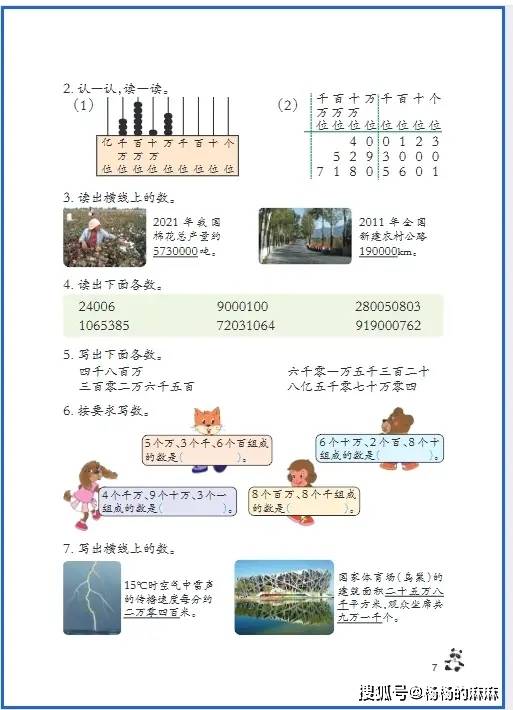
1. 大数认知：构建 “亿级” 数感体系

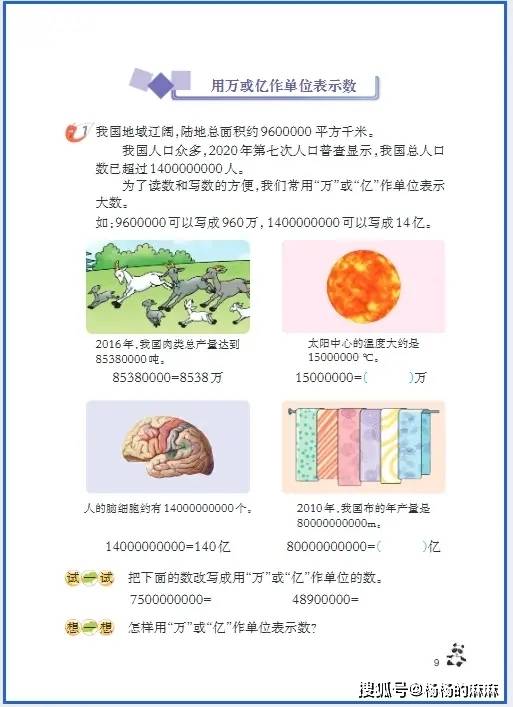
关键任务是突破 “万以内数” 的认知局限，掌握亿以内（及以上）数的读写逻辑（需借助分级法，如将 “50800600” 分为 “万级 5080” 和 “个级 0600”，避免读写错误）、单位改写（如将 “7890000” 改写成 “789 万”，“30500000000” 改写成 “305 亿”），以及 “四舍五入法” 求近似数（如将 “64870” 近似到万位为 “6 万”，“65870” 近似到万位为 “7 万”），核心是理解 “十进制计数法” 中 “相邻计数单位间进率为 10” 的本质，避免数位混淆。

1. 复杂乘除运算：笔算与巧算的 “能力分水岭”

• 三位数乘两位数：需熟练掌握笔算流程（如计算 “234×15” 时，先算 “234×5”，再算 “234×10”，最后错位相加），重点突破 “因数中间或末尾有 0” 的特殊情况（如 “305×24”“230×40”），同时理解 “积的变化规律”（如一个因数不变，另一个因数乘 10，积也乘 10），能快速判断积的位数与大致范围。
• 除数是两位数的除法：核心是掌握 “试商与调商” 技巧 —— 用 “四舍法” 试商（如 “324÷31”，把 31 看作 30 试商）、“五入法” 试商（如 “285÷29”，把 29 看作 30 试商），并理解 “商不变的性质”（如 “480÷40=12”，则 “48÷4=12”“960÷80=12”），避免因试商不当导致计算反复。

1. 运算律应用：从 “硬算” 到 “巧算” 的跨越

重点是理解并灵活运用五大运算律：加法交换律（如 “25+38=38+25”）、加法结合律（如 “18+27+33=18+(27+33)”）、乘法交换律（如 “15×24=24×15”）、乘法结合律（如 “25×12=25×4×3”）、乘法分配律（如 “(100+2)×35=100×35+2×35”），核心是能主动识别 “可凑整” 的算式（如 “99×46=100×46-1×46”“125×88=125×8×11”），通过运算律简化计算，提升效率与准确性。

1. 小数初步认识：打开 “小数世界” 的大门

关键是理解小数的意义（如 “0.6” 表示 “6 个 0.1”，“1.25” 表示 “1 个 1 和 25 个 0.01”），掌握小数的读写（如 “0.035” 读作 “零点零三五”，“五点零二” 写作 “5.02”）、大小比较（如 “0.7＞0.69”，需注意 “小数位数多≠数值大”），以及简单的小数加减法（如 “3.2+1.58=4.78”，需对齐小数点），为五年级小数的深入学习（如小数乘除、小数四则混合运算）奠定基础。

二、图形与几何：空间观念的 “系统构建期”

该模块核心是帮助学生从 “直观看图形” 升级为 “精准描述、规范操作图形”，建立初步的空间逻辑思维。

1. 角的度量与分类：几何学习的 “工具基础”

首先需明确直线（无端点、无限长）、射线（1 个端点、无限长）、线段（2 个端点、有限长）的区别；其次掌握角的分类标准 —— 锐角（小于 90°）、直角（等于 90°）、钝角（大于 90° 且小于 180°）、平角（等于 180°）、周角（等于 360°），避免混淆 “平角与直线”“周角与射线”；最后要熟练使用量角器（“两重合”：中心点与角的顶点重合、0 刻度线与角的一条边重合）量角、画角（如画 “135° 的钝角”，可先画 90° 角，再叠加 45° 角），确保度数准确。

1. 平行四边形与梯形：特殊四边形的 “特征辨析”

核心是抓住两类图形的 “本质特征”：平行四边形需满足 “两组对边分别平行且相等”（如长方形、正方形是特殊的平行四边形），梯形需满足 “只有一组对边平行”（注意 “只有” 二字，避免与平行四边形混淆）；同时要学会规范画 “高”—— 从图形一条边上的任意一点向对边作垂线，这点与垂足之间的线段即为高（如给平行四边形画高时，需明确 “对应的底”，不同的底对应不同的高），避免高的画法错误。

1. 位置与方向：用数学语言 “描述空间”

关键是掌握 “方向 + 距离” 的二维定位法：能根据 “东、南、西、北、东北、东南、西北、西南” 八个基本方向，结合 “偏角”（如 “东偏南 20°”“西偏北 45°”）和 “距离”（如 “300 米”“500 米”）确定物体位置（如 “学校在图书馆东偏北 30° 方向 400 米处”）；同时能根据给定的位置信息，描述简单的路线图（如 “从家出发，向南走 200 米到菜市场，再向东走 300 米到学校”），核心是培养 “空间方位感”，避免方向混淆或距离遗漏。

三、统计与概率：数据分析意识的 “萌芽培育期”

该模块的核心不是 “会画统计图”，而是 “能通过数据解决问题”，培养 “用数据说话” 的意识。

1. 条形统计图：直观呈现 “数据差异”

需掌握单式条形统计图（仅呈现一组数据，如 “班级同学身高分布”）和复式条形统计图（同时呈现两组或多组数据，如 “男、女生身高分布对比”）的绘制要点 —— 横轴标注 “类别”、纵轴标注 “数量”、条形宽度一致、图例清晰（复式统计图需用不同颜色 / 样式区分数据组）；更重要的是能 “解读数据”：从图中提取 “最多 / 最少数据”“数据差值”“数据分布趋势”（如 “140-145 厘米身高的同学最多，130 厘米以下的最少”），并能结合实际问题分析原因（如 “为什么男生 150 厘米以上的人数比女生多？”），避免 “只画图、不分析”。

1. 平均数：理解 “数据的代表”

关键是掌握平均数的求法（“总数量 ÷ 总份数”，如 “5 名同学的体重分别是 30kg、32kg、28kg、35kg、25kg，平均体重为 (30+32+28+35+25)÷5=30kg”），更要理解其 “代表性” 与 “局限性”：平均数能反映一组数据的 “整体水平”（如 “班级平均成绩 85 分，说明多数同学成绩在 85 分左右”），但不能代表 “个体情况”（如有的同学高于 85 分，有的低于 85 分）；同时要了解平均数在生活中的应用场景（如 “比赛打分去掉最高分和最低分，再算平均分”，目的是避免极端数据影响结果公平性），能运用平均数解决实际问题（如 “求小组平均植树棵数”“判断某次考试成绩是否高于班级平均”），培养初步的 “数据分析思维”。