人教A版高中数学（第二册）电子课本可以方便大家随时随地预习或复习课本知识，为此，我们找到人教A版高中数学（第二册）新教材电子书教材的全部内容，以高清图片的形式呈现给大家，希望能够提高大家的学习效率。

如需全套电子课本PDF版，请关注公众号“桃李文库”回复：“电子课本”

人教A版高中数学（第二册）新教材电子课本在线阅读（此为截图版，获取是高清版）

高中数学核心重点（全学段通用，适配高考考点）

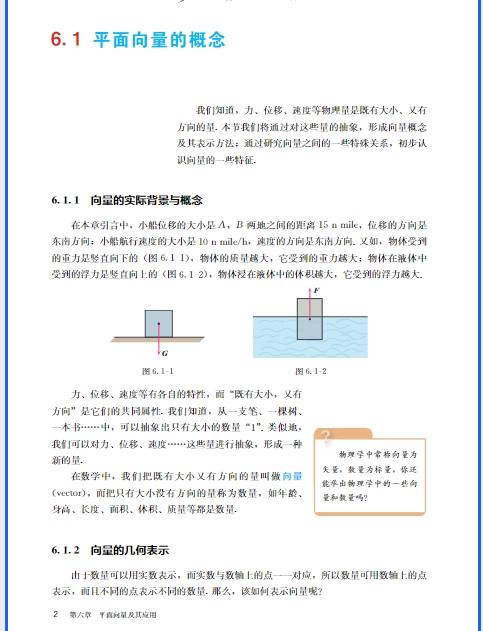
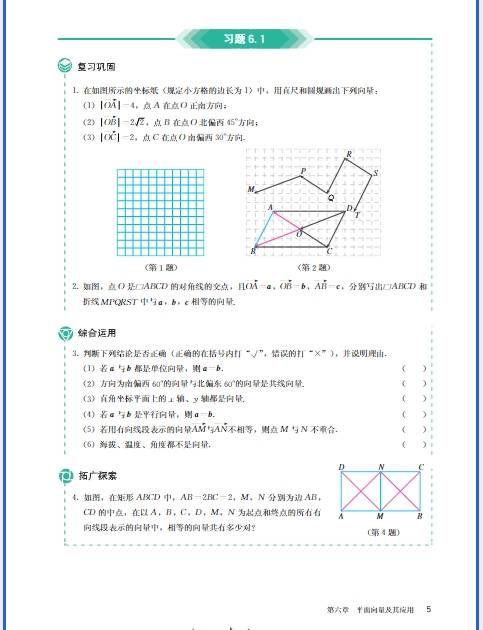
高中数学围绕高考考纲分为函数与导数、三角函数与解三角形、数列、立体几何、解析几何、概率与统计、不等式、平面向量、复数、排列组合与二项式定理十大核心模块，还有选考内容（极坐标与参数方程 / 不等式选讲），整体侧重逻辑推理、数形结合、运算求解、模型建构四大能力。

以下按模块拆解核心考点 + 题型方法 + 学段学习重点，兼顾基础巩固与应试提分，适配高一到高三的学习与复习。

一、函数与导数（高考压轴核心，占分约 20-25 分）

地位：高中数学的 “主线”，贯穿整个高中阶段，导数是函数的延伸，是高考压轴题（解答题最后一题） 必考内容，选择填空也有高频难题。

核心考点

1. 基础函数：指数函数、对数函数、幂函数、二次函数、分段函数的图像与性质（定义域、值域、单调性、奇偶性、周期性、对称性）；
2. 函数综合：函数的零点与方程的根、函数的最值、恒成立 / 能成立问题、数形结合解函数问题；
3. 导数基础：导数的几何意义（求切线方程）、基本初等函数的导数公式、导数的四则运算法则；
4. 导数应用：用导数判断函数单调性、求函数极值与最值、导数解决恒成立 / 存在性问题、导数证明不等式、导数研究函数的零点个数（压轴题核心）。

题型方法

• 单调性判断：导数大于 0 增、小于 0 减，注意定义域优先，含参函数需分类讨论参数范围；
• 切线方程：切点处的导数 = 斜率，分 “已知切点” 和 “未知切点（设切点列方程）” 两种情况；
• 恒成立问题：常转化为求函数的最值（如a≥f(x)恒成立⇔a≥f(x)max）；
• 压轴题技巧：分类讨论、构造函数、放缩法、隐零点代换是解决导数证明 / 零点问题的核心方法。

基础要求

记牢8 大基本导数公式+ 导数运算法则，掌握二次函数、指对函数的图像特征，这是所有函数问题的基础。

二、三角函数与解三角形（基础易得分，占分约 15 分）

地位：高考基础送分模块，选择填空 + 一道解答题（通常第 17 题），题型固定、方法简单，只要记牢公式就能拿高分，极少出难题。

核心考点

1. 三角函数基础：任意角的三角函数定义、同角三角函数的基本关系（sin2α+cos2α=1、tanα=cosαsinα）、诱导公式（“奇变偶不变，符号看象限”）；
2. 三角恒等变换：和差角公式、二倍角公式、辅助角公式（asinx+bcosx=a2+b2sin(x+φ)，必考！）；
3. 三角函数的图像与性质：y=Asin(ωx+φ)+k的图像平移、伸缩变换，求周期、单调区间、对称轴、对称中心、最值；
4. 解三角形：正弦定理、余弦定理、三角形面积公式（S=21absinC），解三角形的实际应用（测量高度、距离、角度）。

题型方法

• 三角恒等变换：核心是 “降幂、化同角、化同名”，辅助角公式是化简的最终常用形式；
• y=Asin(ωx+φ)问题：先通过恒等变换化为标准形式，再求性质，图像平移遵循 “左加右减、上加下减”（只针对x）；
• 解三角形：已知两边一角 / 两角一边用正弦定理，已知三边 / 两边及其夹角用余弦定理，注意三角形内角和为 180°，边角互化是关键。

提分关键

公式烂熟于心，不用死记，