2025年学生将迎来新版教材，新教材将更加重视思维和阅读！为了方便广大学生在暑假预习新学期的课本知识，我们整理了2025新人教版四年级数学（上册）一电子课本，以图片的形式呈现给大家，希望对同学们的暑期学习有所帮助。

以下是部分内容截图，完整信息请查看 PDF 文件

想要帮助四年级学生扎实掌握数学知识、培养逻辑思维，可从 “核心内容概览” 与 “针对性学习方法” 两大维度入手，既理清知识框架，又掌握实用学习技巧，助力平稳度过 “具象运算” 到 “抽象思维” 的过渡阶段（以下内容以人教版教材为参考）。

一、四年级数学核心内容全景梳理

四年级数学在延续低年级基础的同时，新增多个关键知识模块，不仅是对前期内容的深化，更在思维层面提出更高要求，具体可分为四大核心领域：

（一）数与代数：构建复杂运算与数感体系

这一领域是四年级数学的基础，重点在于突破 “大数运算” 与 “运算规律”，建立更系统的数感：

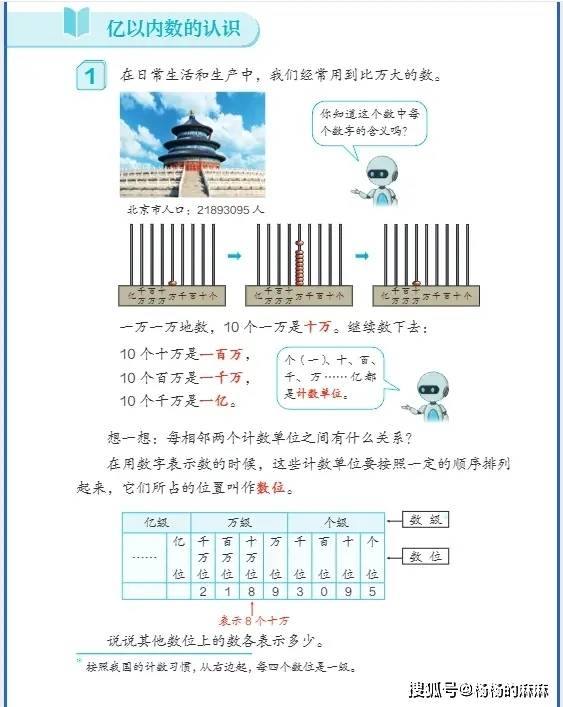
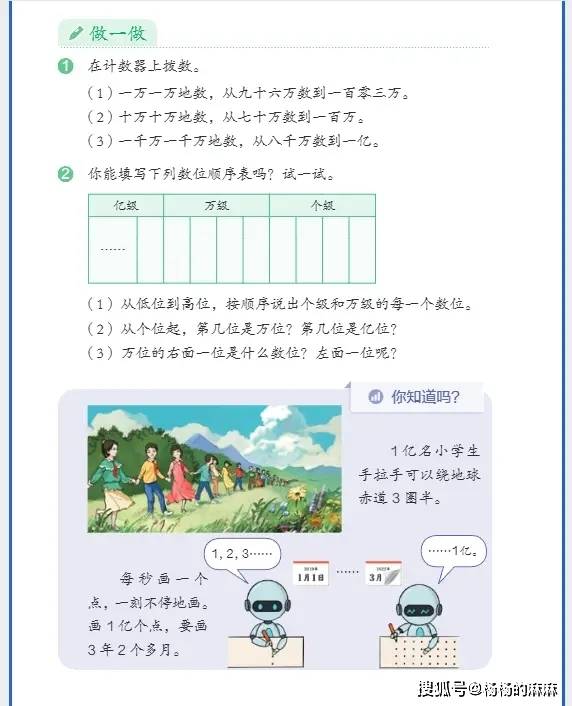
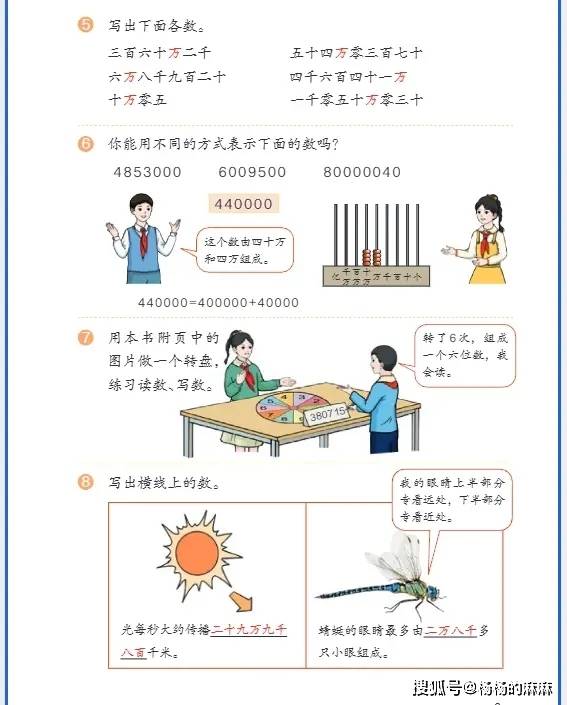
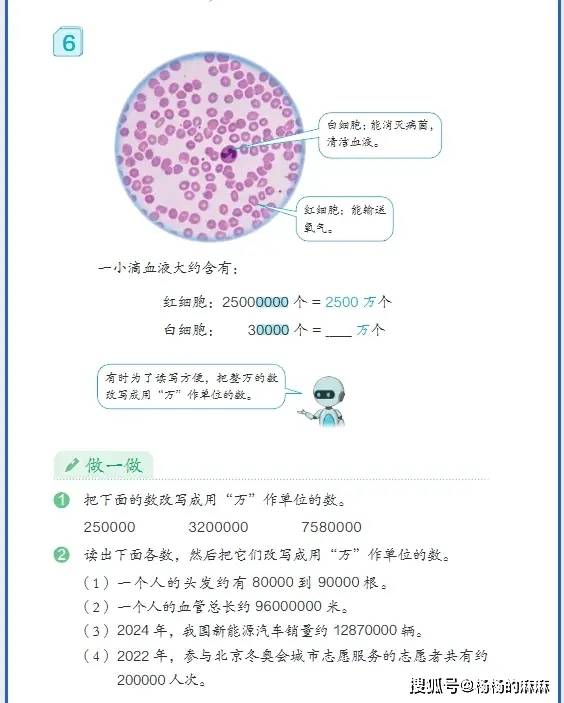
1. 大数的认知与运算：从 “万以内数” 拓展到 “亿以内数”，核心包括亿以内数的读写（含分级读写技巧）、改写（如将整万数改写成用 “万” 作单位）、大小比较，以及十进制计数法的理解（明确数位顺序表中 “亿位”“千万位” 等新数位的意义）；
2. 乘法与除法进阶：掌握 “三位数乘两位数” 的笔算流程（如因数中间或末尾有 0 的特殊情况处理）、积的变化规律（如一个因数不变，另一个因数乘几，积也乘几），以及 “除数是两位数的除法” 笔算（重点突破试商与调商技巧，如 “四舍五入” 试商法）、商的变化规律（如除数不变，被除数乘几，商也乘几）；
3. 运算律的理解与应用：首次系统学习加法交换律、加法结合律，以及乘法交换律、乘法结合律、乘法分配律，核心是理解规律的本质（而非死记公式），并能用于简化计算（如凑整计算）；
4. 小数的初步认知：认识小数的意义（如 0.5 表示 5 个 0.1）、掌握小数的读写方法、小数大小比较（如比较 0.3 和 0.25），以及简单的小数加减法（如 0.8+0.5），为后续小数深入学习打下基础。

能力目标：能熟练进行大数运算，理解运算背后的逻辑，灵活运用运算律简化计算，初步建立小数概念，提升计算的准确性与效率。

（二）图形与几何：培养空间观念与图形操作能力

这一领域聚焦 “图形认知” 与 “空间定位”，强调从 “直观观察” 到 “精准描述” 的过渡：

1. 角的度量与分类：认识直线、射线、线段的区别与联系，掌握角的定义（由一点引出两条射线组成的图形），学习角的分类（锐角、直角、钝角、平角、周角），并能正确使用量角器测量角的度数、画指定度数的角；
2. 平行四边形与梯形的深入学习：明确平行四边形（两组对边分别平行）、梯形（只有一组对边平行）的定义与特征，学会画图形的高（如给平行四边形画不同底对应的高），理解两种图形的联系与区别；
3. 位置与方向的实际应用：能根据 “方向（如东偏北 30°）” 和 “距离” 确定物体的具体位置，会描述简单的路线图（如从学校到公园的行走路线），学会用数学语言精准表达空间位置关系。

能力目标：建立清晰的空间观念，能准确识别、操作几何图形，掌握图形测量与绘制的基本方法，能用数学工具描述物体位置与路线。

（三）统计与概率：提升数据收集与分析能力

这一领域重点在于 “数据解读” 与 “统计工具使用”，培养数据分析意识：

1. 条形统计图的应用：学习单式条形统计图（用一个条形表示一组数据）和复式条形统计图（用两种颜色 / 样式的条形表示两组数据）的绘制方法，能从统计图中提取关键信息（如最多、最少、相差多少），并进行简单的数据分析（如比较两个班级的考试成绩分布）；
2. 平均数的理解与计算：认识平均数的意义（一组数据的总和除以数据个数），掌握平均数的求法，能运用平均数解决实际问题（如计算班级同学的平均身高），理解平均数在生活中的应用场景（如比赛打分去掉最高分和最低分后求平均）。

能力目标：能独立收集、整理数据，熟练使用条形统计图呈现数据，通过平均数和统计图分析数据背后的信息，培养用数据说话的意识。

（四）数学广角：锻炼逻辑推理与策略优化思维

这一领域以 “实际问题” 为载体，培养解决复杂问题的思维能力：

1. 优化问题：通过 “沏茶问题”（如何合理安排步骤，节省时间）、“烙饼问题”（如何安排烙饼顺序，使时间最短），学习 “合理安排时间” 的策略，理解 “同时做”“最优顺序” 等优化思想；
2. 鸡兔同笼问题：掌握用 “列表法”（逐一列举可能的鸡兔数量）、“假设法”（假设全是鸡或全是兔，再调整）解决经典的鸡兔同笼问题，培养逻辑推理与数学建模能力。

能力目标：能运用优化策略解决生活中的时间安排问题，通过列表、假设等方法解决复杂的数学问题，提升逻辑思维与问题解决能力。

二、四年级数学针对性高效学习方法

四年级数学难度明显提升，单纯依靠 “大量刷题” 难以形成长效学习能力，需结合知识特点与学生认知规律，从 “理解、习惯、应用” 三个层面入手：

1. 深耕 “计算核心”，告别 “粗心陷阱”

计算是四年级数学的 “基石”（如三位数乘两位数、除数是两位数的除法），很多学生将错误归咎于 “粗心”，实则是 “算理不清” 与 “习惯不规范” 双重问题：

• 先懂算理，再练技巧：学习新运算时，不急于练题，而是先通过具象工具理解算理。比如学 “三位数乘两位数”，可用 “点子图” 拆分因数（如 132×25=132×20+132×5），让学生直观看到 “为什么竖式计算要错位相加”；学 “除数是两位数的除法”，用 “小棒分一分” 的方式，理解 “试商” 的本质是 “估算每份能分多少”；
• 规范书写，减少失误：要求计算时做到 “三对齐”（竖式计算数位对齐、横式结果与算式对齐、草稿纸书写分区对齐），避免因字迹潦草、数字错位导致错误；每天安排 10-15 分钟 “精准计算练习”，选择典型易错题型（如因数末尾有 0 的乘法、除数接近整十数的除法），强调 “算一步查一步”（如算完乘法后，用除法验算），而非全部做完再检查；
• 巧用运算律，简化计算：引导学生主动用运算律简化复杂计算，比如计算 “99×37+37” 时，可转化为 “37×(99+1)=37×100=3700”，既提升计算速度，又加深对运算律的理解；遇到 “125×32×25” 这类题，可拆分为 “125×8×4×25=(125×8)×(4×25)=1000×100=10000”，培养 “凑整” 思维。

2. 拆解 “几何难点”，从 “直观” 到 “抽象” 过渡

四年级几何知识对空间观念要求较高，学生易因 “理解不透彻” 导致错误，可通过 “观察 - 操作 - 描述” 三步法突破：

• 多观察，建立图形认知：日常引导学生观察生活中的几何图形（如窗户是长方形、自行车车架是三角形、楼梯栏杆是平行四边形），让抽象图形与实际物体关联；学习 “角的度量” 时，用吸管制作可活动的角，直观感受 “角的大小与边的长短无关，与两边张开程度有关”；
• 多动手，强化操作能力：画几何图形时，严格要求使用工具（量角器、直尺），比如画平行四边形的高，先让学生标注 “底”，再用三角板的直角边对齐底，画出垂直的高；学习 “位置与方向” 时，用方格纸模拟场景，让学生亲手标注物体位置、绘制路线图，在操作中理解 “方向与距离” 的作用；
• 多描述，提升数学表达：鼓励学生用准确的数学语言描述图形特征，比如描述梯形时，要说 “只有一组对边平行的四边形”，而非 “有一组对边平行的四边形”；描述角的度数时，要说 “这个角是 60 度的锐角”，培养精准表达的习惯。

3. 破解 “应用题难关”，从 “读题” 到 “解题” 闭环

四年级应用题难度提升，涉及多步骤计算与复杂数量关系，学生易因 “读不懂题”“理不清关系” 丢分，可按 “四步解题法” 训练：

• 圈画关键信息：读题时用横线标出 “已知条件”（如 “小明有 35 元，买文具花了 12 元”），用波浪线标出 “问题”（如 “还剩多少元”），避免遗漏信息；遇到 “比多比少”“倍数关系” 类题目，重点圈出 “比”“倍” 等关键词（如 “小红的书比小明多 5 本”“苹果的数量是梨的 3 倍”）；
• 梳理数量关系：用 “线段图” 或 “文字关系式” 理清条件与问题的联系，比如 “学校买了 4 箱粉笔，每箱 24 盒，用去 38 盒，还剩多少盒”，可列出关系式 “总盒数 - 用去盒数 = 剩余盒数”，再代入数据计算；遇到多步骤应用题（如 “先算总量，再算部分量”），分步写出每一步的计算目标（如第一步算 “4 箱粉笔共多少盒”，第二步算 “剩余多少盒”）；
• 验证解题结果：算出答案后，引导学生 “反向验证”，比如 “小明有 23 元，买笔花了 8 元，剩下的钱买了 3 本笔记本，每本笔记本多少元”，算出 “每本 5 元” 后，可反向计算 “3×5+8=23 元”，与已知条件一致则说明答案正确；
• 总结题型规律：定期整理同类应用题（如 “购物问题”“行程问题”“工程问题”），总结解题思路，比如 “行程问题” 常用 “路程 = 速度 × 时间”“时间 = 路程 ÷ 速度” 等关系式，让学生遇到同类题目时能快速定位解题方法。

4. 用好 “统计工具”，培养数据分析思维

统计与概率模块易被忽视，实则是培养 “数据意识” 的关键，学习时需注重 “实操” 与 “分析” 结合：

• 亲手制作统计图：不依赖现成的统计图，让学生从 “收集数据” 开始（如调查班级同学的生日月份、喜欢的运动），用直尺和铅笔绘制条形统计图，过程中注意 “横轴标类别、纵轴标数量、条形宽度一致”，在操作中理解统计图的结构；
• 深入解读数据信息：观察统计图时，不仅要能说出 “最多”“最少”，还要能分析 “为什么最多”“两者相差多少”“整体趋势如何”，比如从 “班级同学身高统计图” 中，分析 “140-145 厘米的同学最多，可能是因为这个年龄段的孩子普遍处于该身高区间”；
• 结合生活理解平均数：通过实际案例理解平均数的 “代表性” 与 “局限性”，比如 “班级同学的平均身高是 142 厘米，不代表每个同学都是 142 厘米，有的比平均高，有的比平均矮”；计算 “比赛打分” 时，解释 “去掉最高分和最低分” 的原因（避免极端分数影响公平性），让学生明白平均数在生活中的实际意义。

5. 攻克 “数学广角”，锻炼逻辑与策略思维

数学广角的题目更注重 “思维方法”，而非 “计算能力”，学习时需避免 “死记解法”，而是理解 “解题逻辑”：

• 用 “枚举法” 突破优化问题：学 “烙饼问题” 时，让学生列举 “烙 2 张饼”“烙 3 张饼” 的不同方法（如一张一张烙、两张同时烙），计算每种方法的时间，对比得出 “最优策略”（烙 3 张饼时，交替烙最省时间）；学 “沏茶问题” 时，用 “流程图” 列出所有步骤，标记 “可同时做的步骤”（如烧水时洗茶杯、找茶叶），理解 “优化” 的本质是 “合理利用时间”；
• 用 “假设法” 破解鸡兔同笼：面对 “鸡兔同笼，共 10 头，32 脚” 的问题，先引导学生 “假设全是鸡”（则有 20 只脚），发现 “少了 12 只脚”，再分析 “每把一只鸡换成兔，增加 2 只脚”，从而算出 “需要换 6 只兔”，过程中用 “画图法” 辅助理解（用圆圈表示头，用竖线表示脚），让抽象的假设过程变得直观。

通过以上对核心内容的系统梳理与针对性学习方法的落地，四年级学生不仅能扎实掌握数学知识，更能逐步培养 “理解算理、逻辑推理、数据分析、问题解决” 的数学思维，为后续更高年级的数学学习奠定坚实基础。