2025年学生将迎来新版教材，新教材将更加重视思维和阅读！为了方便广大学生在暑假预习新学期的课本知识，我们整理了2025新冀教版五年级数学（上册）一电子课本，以图片的形式呈现给大家，希望对同学们的暑期学习有所帮助。

以下是部分内容截图，完整信息请查看 PDF 文件

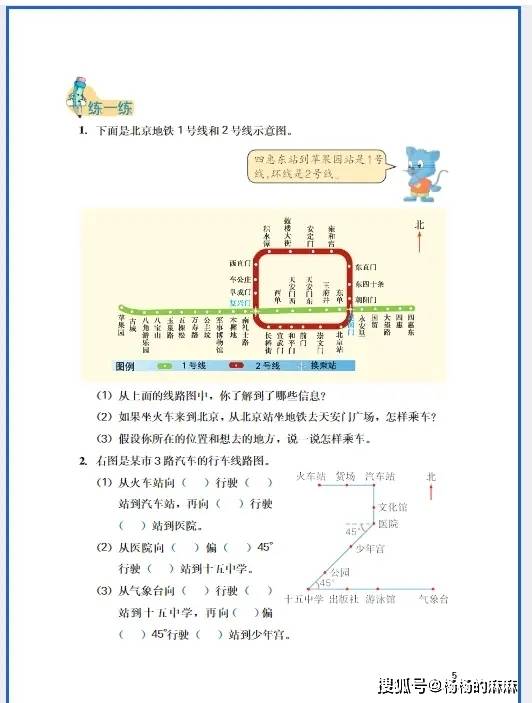
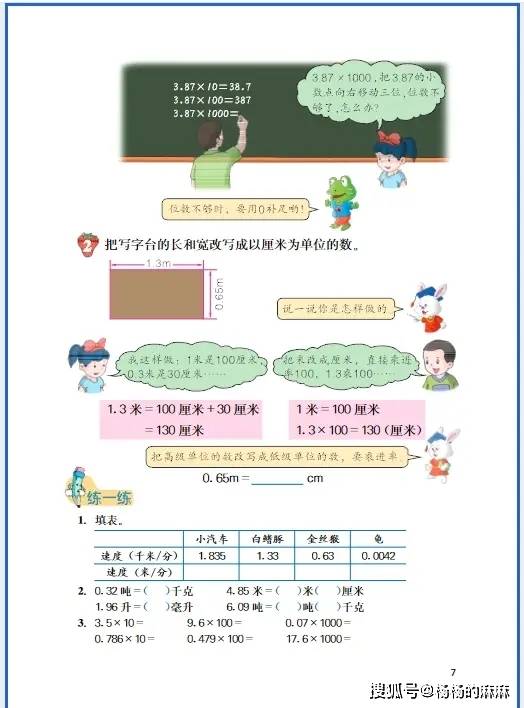
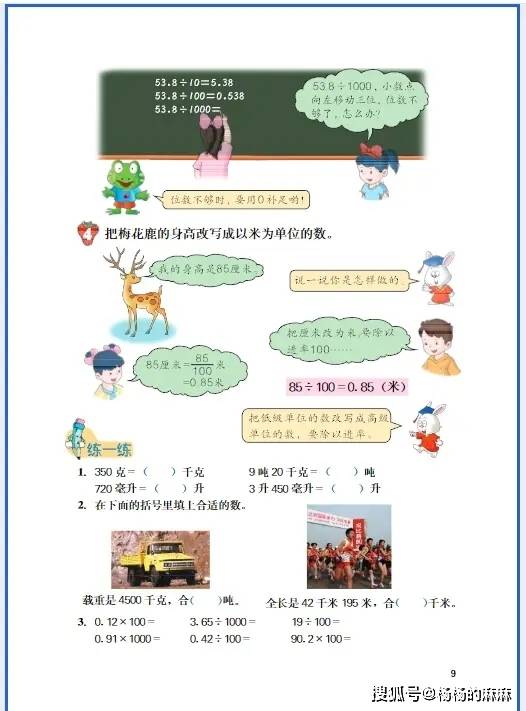
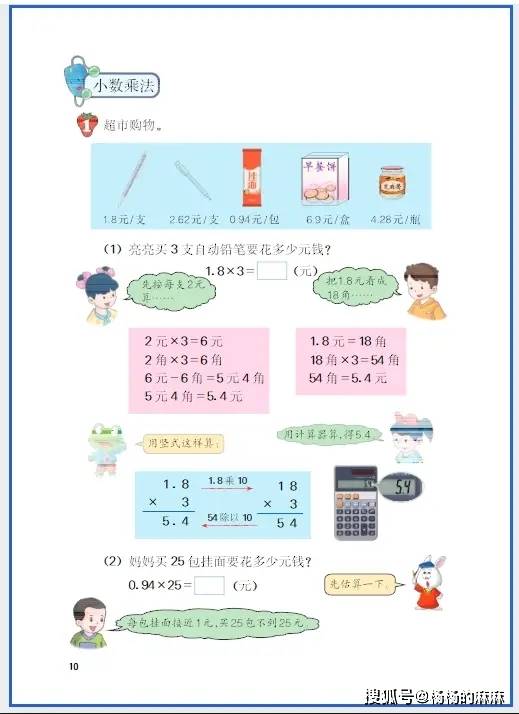
五年级计算题是数学学习的 “基本功训练场”，核心围绕整数四则混合运算的深化、小数运算的入门以及分数运算的初步接触展开。不同题型的计算逻辑和操作要点差异较大，需先明确题型特征，再匹配对应的解题方法，避免盲目计算。

一、先辨题型：找准计算核心方向

五年级计算题主要可分为三大类，每类题型的核心考点和解题思路各有侧重，需精准区分：

• 整数四则混合运算：核心考点是 “运算顺序的严格遵循”，需牢记 “有括号先算括号内，无括号时先算乘除、后算加减，同级运算（只有加减或只有乘除）从左到右依次计算”，解题时需按顺序分步推进，不可随意跳步。
• 小数加减法：核心考点是 “相同数位对齐”，而实现这一目标的关键是 “小数点对齐”，无论是整数与小数相加，还是小数与小数相加，都需先将小数点上下对齐，再从末位开始计算，必要时可通过末尾补 0 补全小数位数，确保计算准确。
• 小数乘除法：核心考点是 “小数点的定位”。小数乘法需先将小数转化为整数计算乘积，再根据因数中小数的总位数确定积的小数点位置；小数除法需先将除数转化为整数，被除数同步扩大相同倍数，再按整数除法规则计算，商的小数点位置需与转化后被除数的小数点对齐。
• 分数运算：五年级主要涉及同分母分数加减法、异分母分数加减法以及分数与整数相乘。其中，同分母分数加减法核心是 “分母不变，只算分子加减”；异分母分数加减法核心是 “先通分，转化为同分母分数后再计算”；分数与整数相乘核心是 “分子与整数相乘，分母保持不变，能约分的先约分再计算更简便”。

二、严守步骤：掌握每类题型的标准解法

计算题的正确率离不开规范的解题步骤，以下针对五年级高频计算题类型，详细拆解 “分步操作指南”，按步骤执行可大幅减少基础错误。

（一）整数四则混合运算：“标顺序→分步算→细检查”

这类运算的关键是不混淆运算顺序，尤其当算式中出现多层括号或多步乘除时，需按 “优先级” 逐步计算：

1. 标顺序：拿到算式后，先用不同符号标注出运算步骤的优先级，比如用 “△” 标出括号内的运算，用 “○” 标出乘除运算，用 “□” 标出加减运算，明确先算什么、再算什么。

示例：计算

360−(24A

~

5+18)A

~

⋅6

，先标括号内的 “24×5”（△1）和 “24×5 + 18”（△2），再标括号外的 “(△2) ÷ 6”（○1），最后标 “360 - (○1)”（□1）。

1. 分步脱式：严格按标注的顺序逐步书写计算过程，每一步只完成一个运算，且要完整写出当前算式，避免直接写结果。

延续示例：

360−(24A

~

5+18)A

~

⋅6

=360−(120+18)A

~

⋅6

（先算括号内乘法：24×5=120）

=360−138A

~

⋅6

（再算括号内加法：120+18=138）

=360−23

（接着算除法：138÷6=23）

=337

（最后算减法：360-23=337）

1. 避坑点：绝对不能跳步计算，比如直接将 “(24×5 + 18) ÷ 6” 算成 “(120+18)÷6=23” 后，跳过 “360 - 23” 这一步直接写结果；同时注意括号的优先级高于乘除，不可先算括号外的除法再算括号内的运算。

（二）小数加减法：“对齐点→补零位→算进退”

核心是通过 “小数点对齐” 确保相同数位对齐，计算时需关注末位的进位和退位情况：

1. 对齐点：列竖式时，将两个数的小数点上下严格对齐，若其中一个数是整数（如 4），需先在整数末尾添上小数点和 0（写成 4.0 或 4.00），使两个数的小数位数一致。

示例 1（加法）：计算 5.32 + 2.8

先将竖式写成：

plaintext

取消自动换行

复制

• 2.80

plaintext

取消自动换行

复制

（2.8末尾补0成2.80，确保与5.32都是两位小数，小数点对齐）

1. 算进退：从末位开始计算，加法中满 10 向前一位进 1，减法中不够减向前一位借 1 当 10，进位和借位需在竖式中清晰标注（如进位用 “1” 标在对应数位上方，借位用 “・” 标在对应数位上方）。

延续示例 1 加法计算：

百分位：2+0=2；

十分位：3+8=11，满 10 向个位进 1，十分位写 1，个位上方标 “1”；

个位：5+2+1（进位）=8；

最后在结果对应位置点上小数点，得 8.12。

示例 2（减法）：计算 6 - 3.15

先将 6 写成 6.00，竖式对齐：

plaintext

取消自动换行

复制

6.00

• 3.15

plaintext

取消自动换行

复制

百分位：0减5不够减，向十分位借1当10，10-5=5，十分位上方标“·”；

十分位：原本是0，被借走1后剩9，9减1=8；

个位：6被借走1后剩5，5减3=2；

结果得 2.85。

1. 避坑点：切忌将 “末尾对齐” 当作 “数位对齐”，比如计算 5.32 + 2.8 时，将 2.8 的 “8” 与 5.32 的 “2” 对齐（末位对齐），导致十分位的 “8” 与百分位的 “2” 错位，最终计算错误。

（三）小数乘除法：“转整数→定点位→理特殊”

这类运算的核心是通过 “转化” 将小数计算变为整数计算，再处理小数点问题，同时需关注特殊情况的应对：

1. 小数乘法：“转整数算积→数小数位数→点小数点”

1. 转整数：忽略两个因数的小数点，将其当作整数进行乘法计算，求出整数乘积。

示例：计算 3.25 × 0.4

先算 325 × 4 = 1300（忽略小数点，3.25 变 325，0.4 变 4）。

1. 数位数：分别数出两个因数中小数的位数，将位数相加，得到积需要保留的小数总位数。

延续示例：3.25 有 2 位小数，0.4 有 1 位小数，总共 2+1=3 位小数。

1. 点小数点：从整数乘积的末位开始，向左数出对应位数（示例中数 3 位），点上小数点；若整数乘积的位数不够，则在前面补 0，再点小数点。

延续示例：1300 从末位向左数 3 位，是 1.300，末尾的 0 可省略，得 1.3。

特殊情况（积的位数不够）：计算 0.15 × 0.02

整数乘积：15×2=30；

因数共 2+2=4 位小数，30 只有 2 位，需在前面补 2 个 0，变成 0.0030，省略末尾 0 后得 0.003。

1. 避坑点：点小数点时方向不能错（必须从末位向左数），且不能遗漏因数中的小数位数，比如计算 3.25×0.4 时，误将小数位数算成 2+0=2 位，得到 13.00 的错误结果。

2. 小数除法：“转整数除数→同步变被除数→算商定位”

根据除数是否为整数，分为两种情况，核心都是先将除数转化为整数：

类型 A：除数是整数（如 7.2 ÷ 4）

1. 列竖式：将被除数写在除号内，除数写在除号外，商的小数点位置需与被除数的小数点位置上下对齐。
2. 分步计算：从被除数的最高位开始除起，若整数部分不够除（如 0.96 ÷ 3），需先在商的整数部分写 0，再点上小数点，继续除小数部分。

示例：计算 0.96 ÷ 3

竖式中，3 除 0 不够除，商 0，点小数点；

3 除 9 得 3，写在十分位；

3 除 6 得 2，写在百分位；

结果得 0.32。

类型 B：除数是小数（如 4.5 ÷ 0.15）

1. 转整数除数：看除数有几位小数，就将除数的小数点向右移动几位，使其变成整数（0.15 有 2 位小数，向右移 2 位变成 15）。
2. 同步变被除数：被除数的小数点需同步向右移动相同位数，若被除数的小数位数不够，则在末尾补 0（4.5 有 1 位小数，向右移 2 位需补 1 个 0，变成 450）。
3. 算商：按整数除法的规则计算（450 ÷ 15 = 30），商的小数点无需额外调整（因被除数已同步变化），直接得 30。

特殊情况（商中间有 0）：计算 3.06 ÷ 6

6 除 3 不够除，商 0，点小数点；

6 除 0 得 0，写在十分位；

6 除 6 得 1，写在百分位；

结果得 0.51。

1. 避坑点：转化除数时，被除数必须同步扩大相同倍数，且扩大后若位数不够需补 0，比如计算 1.2 ÷ 0.25 时，除数变 25（右移 2 位），被除数需变 120（右移 2 位，补 1 个 0），不可误将被除数变成 12 导致计算错误。

（四）分数运算：“分类型→按规则→简约分”

五年级分数运算以基础加减和整数乘法为主，需根据题型遵循不同规则，同时灵活运用约分简化计算：

1. 同分母分数加减法：“分母不变→分子加减→约最简”

1. 计算分子：保持两个分数的分母不变，只将分子进行相加或相减，得到新的分子。

示例：

8

3

+8

2

，分母保持 8 不变，分子 3+2=5，得

8

5

；

9

7

−9

4

，分母保持 9 不变，分子 7-4=3，得

9

3

。

1. 约最简：若计算结果的分子和分母有公因数（如
2. 9
3. 3
5. ），需用公因数（3）同时除以分子和分母，化简为最简分数（
6. 3
7. 1
9. ）。
10. 避坑点：不可将分母也进行加减，比如
11. 8
12. 3
13. +8
14. 2
16. 误算成
17. 8+8
18. 3+2
19. =16
20. 5
22. ，这是完全错误的。

2. 异分母分数加减法：“找最小公倍数→通分变同分母→按同分母算”

1. 找最小公倍数：确定两个分母的最小公倍数，作为通分后的共同分母（如计算
2. 4
3. 1
4. +3
5. 2
7. ，4 和 3 的最小公倍数是 12）。
8. 通分：将每个分数的分子和分母同时乘一个数，使分母变成最小公倍数，分子同步变化（
9. 4
10. 1
12. 的分子分母同乘 3，得
13. 12
14. 3
16. ；
17. 3
18. 2
20. 的分子分母同乘 4，得
21. 12
22. 8
24. ）。
25. 计算：按同分母分数加减法规则计算，分子相加（3+8=11），分母保持 12 不变，得
26. 12
27. 11
29. ，若需约分再进一步化简（此例已是最简）。
30. 避坑点：通分时分子必须同步乘与分母相同的数，比如
31. 4
32. 1
34. 通分成分母 12 时，只将分母乘 3，分子仍为 1，得到
35. 12
36. 1
38. ，导致后续计算错误。

3. 分数与整数相乘：“辨能否约分→先约再算或直接算→定结果”

1. 直接计算（不能约分时）：将整数与分数的分子相乘，分母保持不变，结果若为假分数可转化为带分数（如
2. 5
3. 2
4. A
5. ~
6. 3
7. ，分子 2×3=6，分母 5 不变，得
8. 5
9. 6
11. ，转化为
12. 15
13. 1
15. ）。
16. 先约分再计算（能约分时）：若整数与分数的分母有公因数，先将整数与分母约分，再用约分后的整数与分子相乘，简化计算过程（如
17. 7
18. 3
19. A
20. ~
21. 14
22. ，14 和 7 的公因数是 7，14÷7=2，7÷7=1，再算 3×2=6，分母 1 不变，直接得 6）。
23. 避坑点：只能将整数与分母约分，不可将整数与分子约分（如
24. 7
25. 3
26. A
27. ~
28. 14
29. 误将 14 与分子 3 约分，导致结果错误）；同时注意整数与分母约分后，分母变为 1 时，结果直接为整数，无需保留分母。