2025年学生将迎来新版教材，新教材将更加重视思维和阅读！为了方便广大学生在暑假预习新学期的课本知识，我们整理了2025新

北师大版八年级数学（上册）一电子课本，以图片的形式呈现给大家，希望对同学们的暑期学习有所帮助。

如需全套电子课本PDF版，请关注公众号“桃李科普”回复：“电子课本”

北师大版八年级数学（上册）电子课本在线阅读

8 年级（初二）数学是初中知识的 “进阶阶段”，核心是从 “代数计算” 向 “代数逻辑” 过渡，同时新增 “几何证明” 和 “函数入门”，难度较 7 年级明显提升。以下从 重点知识模块、高频难点、学习策略 三方面整理，帮你搭建清晰的知识框架：

一、8 年级数学核心知识模块（按学期拆分，贴合教材）

（一）8 年级上册：代数深化 + 几何证明入门

1. 三角形（几何核心，证明题基础）

• 核心内容：

1. 三角形的性质：内角和 180°、外角和 360°，任意两边之和大于第三边（常考 “三边能否构成三角形”，如 “3、4、5 可以，2、3、6 不可以”）；
2. 特殊三角形：

• 等腰三角形：两腰相等、两底角相等（“等边对等角”“等角对等边”），三线合一（顶角平分线、底边上的中线、高重合，证明题高频考点）；
• 等边三角形：三边相等、三角均为 60°，任意角的平分线 / 中线 / 高都三线合一；
• 直角三角形：两锐角互余，勾股定理（a2
• +b2
• =c2
• ，c
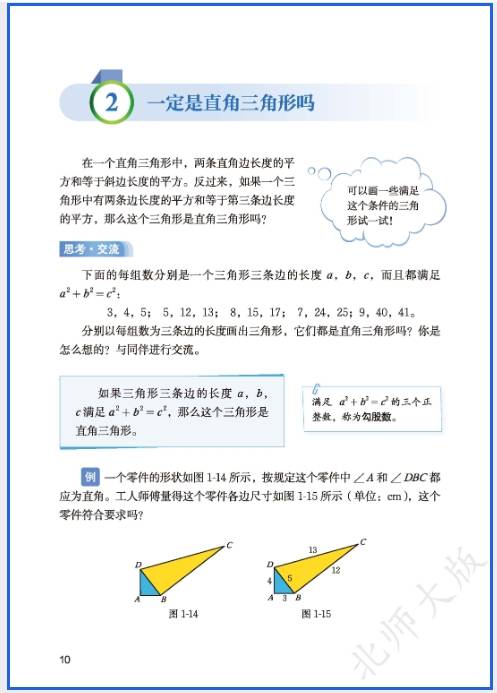
• 为斜边，常考 “已知两边求第三边”，如 3、4、5；5、12、13），勾股定理逆定理（若a2
• +b2
• =c2
• ，则为直角三角形）；

1. 三角形全等（8 上几何重点）：

• 判定定理：SSS（三边对应相等）、SAS（两边及其夹角对应相等，注意 “夹角” 不能错）、ASA（两角及其夹边）、AAS（两角及其中一角的对边）、HL（直角三角形斜边 + 直角边）；
• 作用：证明线段相等、角相等（如 “证明 AB=CD”，可通过证明△ABC≌△DCB 实现）。
• 常考题型：三角形内角 / 外角计算、等腰 / 直角三角形性质应用、全等三角形证明（需写 “已知→求证→证明” 完整步骤）。

2. 轴对称（与三角形结合紧密）

• 核心内容：

1. 轴对称图形：沿某条直线折叠后，直线两旁的部分完全重合（如等腰三角形、正方形、圆）；
2. 轴对称性质：对称轴垂直平分对应点的连线，对应线段相等、对应角相等（常考 “找最短路径”，如 “将军饮马问题”：在直线 l 上找一点 P，使 PA+PB 最短，做法是作 A 关于 l 的对称点 A'，连接 A'B 与 l 的交点即为 P）。

• 常考题型：判断轴对称图形、利用轴对称求最短路径、结合等腰三角形证明线段 / 角关系。

3. 整式的乘法与因式分解（代数重点，衔接分式）

• 核心内容：

1. 整式乘法：

• 同底数幂相乘：am
• ⋅an
• =am+n
• （如23
• ×22
• =25
• ）；
• 幂的乘方：(am
• )n
• =amn
• （如(32
• )3
• =36
• ）；
• 积的乘方：(ab)n
• =an
• bn
• （如(2x)3
• =8x3
• ）；
• 多项式乘多项式：(a+b)(c+d)=ac+ad+bc+bd
• （重点是 “不重不漏”，如(x+2)(x−3)=x2
• −3x+2x−6=x2
• −x−6
• ）；
• 乘法公式（高频考点）：平方差公式(a+b)(a−b)=a2
• −b2
• 、完全平方公式(a±b)2
• =a2
• ±2ab+b2
• （常考 “公式逆用”，如x2
• −4=(x+2)(x−2)
• ，x2
• +6x+9=(x+3)2
• ）；

1. 因式分解（与整式乘法互为逆运算）：

• 步骤：先提公因式（如2x2
• +4x=2x(x+2)
• ），再用公式（平方差、完全平方），分解到不能再分为止；
• 注意：因式分解结果是 “几个整式的积”，不是和或差（如x2
• −1
• 分解为(x+1)(x−1)
• ，不能写成x2
• −1
• ）。
• 常考题型：整式乘法计算、乘法公式应用（化简求值，如 “已知 x+y=5，xy=3，求 x^2+y^2的
• 值
• ，
• 用
• x^2+y^2=(x+y)^2-2xy=25-6=19$）、因式分解（直接分解或结合化简）。

4. 分式（代数拓展，类比分数）

• 核心内容：

1. 分式概念：形如B
2. A
4. （A、B 是整式，B 中含字母且 B≠0），常考 “分式有意义 / 无意义 / 值为 0”：

• 有意义：B≠0；无意义：B=0；值为 0：A=0 且 B≠0（如x+3
• x−2
• 值为 0 时，x=2 且 x≠-3）；

1. 分式性质：B
2. A
3. =B⋅M
4. A⋅M
5. =B÷M
6. A÷M
8. （M≠0，类比分数的基本性质），用于分式化简（如4x2
9. 2x
10. =2x
11. 1
13. ）；
14. 分式运算：乘除（B
15. A
16. ×D
17. C
18. =BD
19. AC
21. ，B
22. A
23. ÷D
24. C
25. =B
26. A
27. ×C
28. D
30. ）、加减（先通分，再分子相加减，如x
31. 1
32. +2x
33. 1
34. =2x
35. 2
36. +2x
37. 1
38. =2x
39. 3
41. ），运算结果要化为最简分式。

• 常考题型：分式有意义 / 值为 0 的条件、分式化简、分式化简求值（如 “已知 x=1，求x+1
• x2
• −1
• 的值，先化简为 x-1，再代入得 0”）。

（二）8 年级下册：函数入门 + 几何进阶

1. 二次根式（代数基础，衔接二次函数）

• 核心内容：

1. 二次根式概念：形如a
3. （a≥0）的式子，常考 “二次根式有意义”：a≥0（如−
4. 有意义时，x≥2）；
5. 二次根式性质：a2
6. =∣a∣
7. （如(−3)2
8. =3
9. ）、ab
10. =a
11. ⋅b
13. （a≥0，b≥0）、b
15. a
17. =b
18. a
21. （a≥0，b>0），用于化简（如12
22. =4×3
23. =23
25. ）；
26. 二次根式运算：加减（先化为最简二次根式，再合并同类二次根式，如23
27. +12
28. =23
29. +23
30. =43
32. ）、乘除（直接用性质计算，如2
33. ×3
34. =6
36. ）。

• 常考题型：二次根式有意义的条件、二次根式化简、二次根式运算。

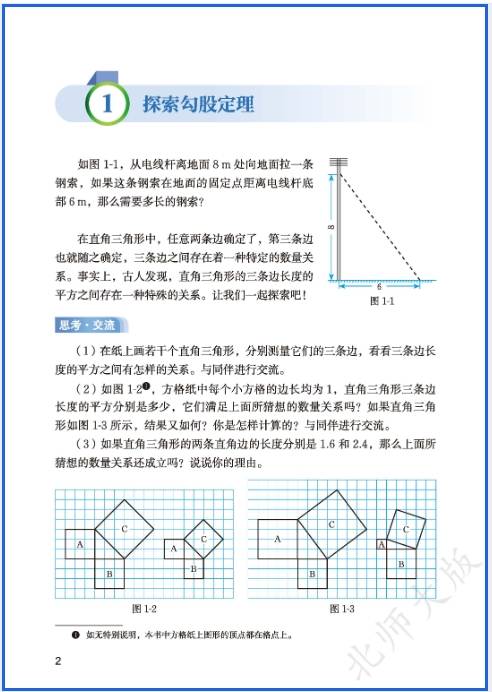
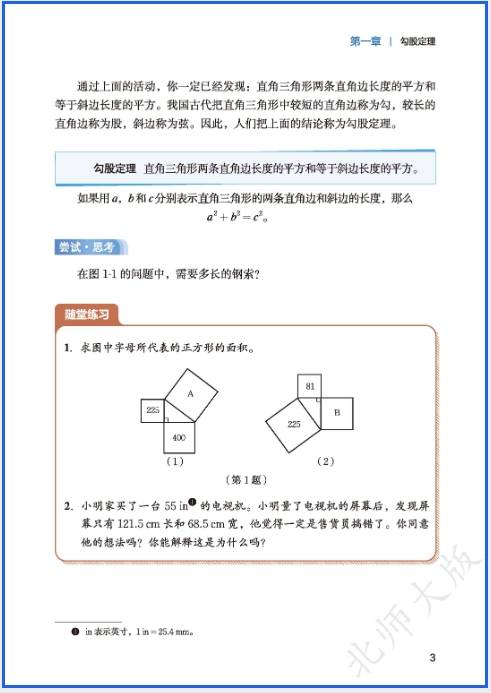
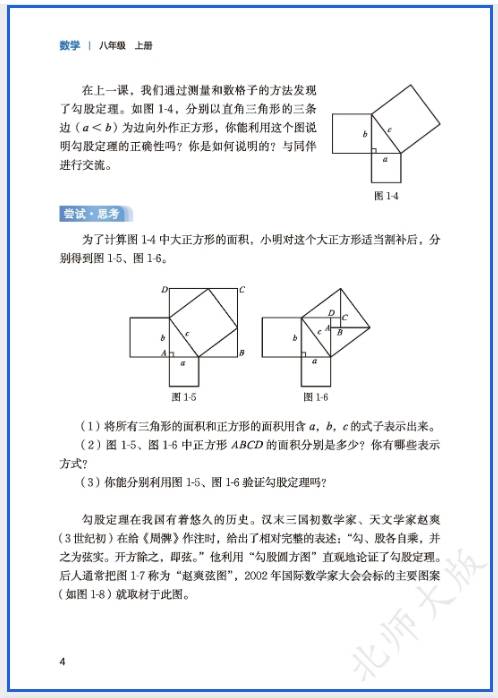
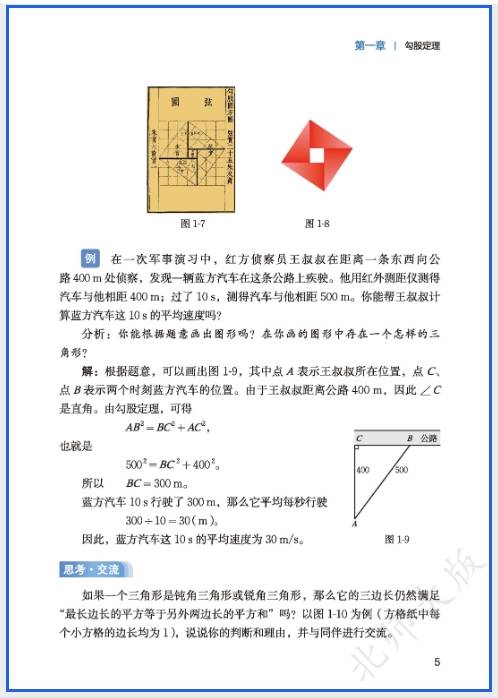
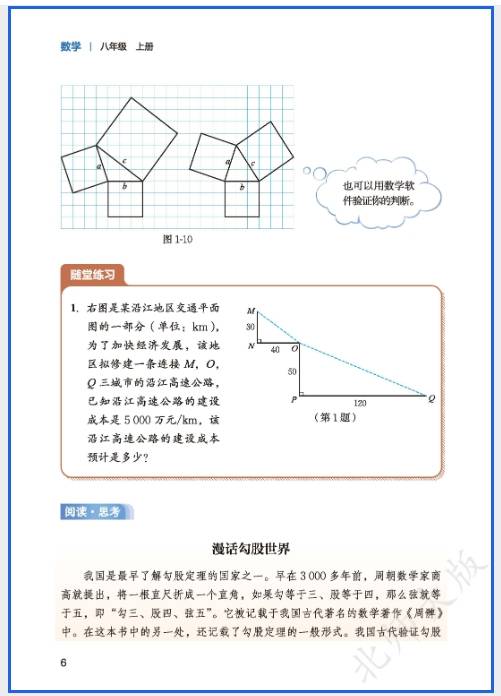
2. 勾股定理（8 上延续，8 下侧重应用）

• 核心内容：除了 8 上的性质和逆定理，8 下重点考 “实际应用” 和 “与坐标系结合”：

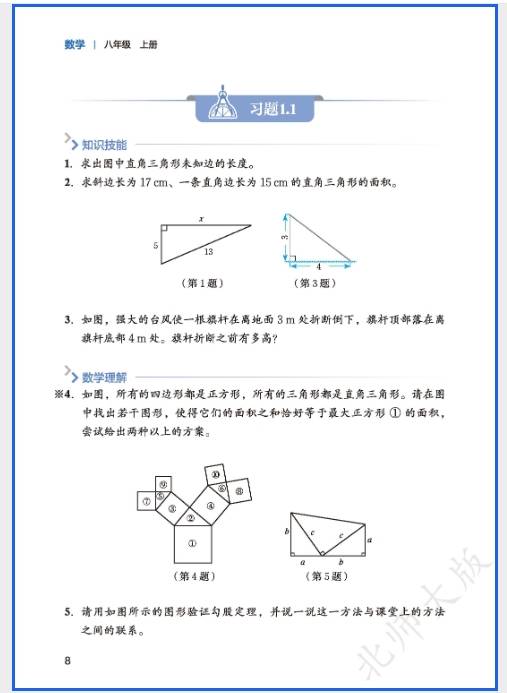
1. 实际应用：如 “梯子靠墙问题”（梯子长 5m，底端距墙 3m，求顶端到地面高度，用勾股定理得 4m）、“折叠问题”（长方形折叠后，利用勾股定理列方程求边长）；
2. 坐标系应用：求两点间距离（如 A (1,2)、B (4,6)，距离 AB=(4−1)2
3. +(6−2)2
4. =9+16
5. =5
6. ）。

• 常考题型：勾股定理实际应用题、坐标系中两点间距离计算。

3. 平行四边形（8 下几何核心，证明 + 计算）

• 核心内容：

1. 平行四边形性质：对边平行且相等、对角相等、对角线互相平分（常考 “利用性质求边长 / 角度”，如 “平行四边形 ABCD 中，AB=5，则 CD=5；∠A=60°，则∠C=60°，∠B=120°”）；
2. 平行四边形判定：两组对边分别平行 / 相等、一组对边平行且相等、两组对角分别相等、对角线互相平分（证明 “四边形是平行四边形” 的关键，需结合全等三角形）；
3. 特殊平行四边形（高频考点）：

• 矩形：平行四边形 + 有一个直角（或对角线相等），性质：四个角都是直角，对角线相等（常考 “矩形对角线相等”，如 “矩形 ABCD 中，AC=10，则 BD=10”）；
• 菱形：平行四边形 + 邻边相等（或对角线互相垂直），性质：四条边相等，对角线互相垂直平分（常考 “菱形面积 = 对角线乘积的一半”，如对角线 6 和 8，面积 = 24）；
• 正方形：矩形 + 菱形，兼具两者所有性质（四条边相等、四个角直角、对角线相等且垂直平分）。
• 常考题型：平行四边形 / 矩形 / 菱形 / 正方形的性质应用、判定证明（如 “证明四边形 ABCD 是矩形”，先证是平行四边形，再证有一个直角或对角线相等）、面积计算。

4. 一次函数（函数入门，初中函数核心）

• 核心内容：

1. 函数概念：两个变量 x、y，对于 x 的每一个值，y 都有唯一确定的值与之对应（常考 “判断是否为函数”，如 “y=2x+1 是函数，x^2+y^2=1 不是，因为一个 x 对应两个 y”）；
2. 一次函数定义：形如y=kx+b
3. （k、b 为常数，k≠0），当 b=0 时，y=kx
4. 是正比例函数（特殊的一次函数）；
5. 一次函数图像与性质：

• 图像：过两点（0,b）和(−k
• b
• ,0)
• 的直线；
• 性质：k>0 时，y 随 x 增大而增大（直线从左到右上升）；k<0 时，y 随 x 增大而减小（直线从左到右下降）；b 决定直线与 y 轴交点（b>0 交 y 轴正半轴，b<0 交负半轴）；

1. 一次函数应用：

• 求解析式：设y=kx+b
• ，代入两点坐标列方程组求解（如 “直线过 (1,3) 和 (2,5)，代入得{k+b=3
• 2k+b=5
• ，解得 k=2，b=1，解析式为 y=2x+1”）；
• 实际应用题：如 “行程问题”“利润问题”，用一次函数表示数量关系，求最值（k>0 时，x 越大 y 越大；k<0 时，x 越小 y 越大）。
• 常考题型：一次函数解析式求解、图像性质应用（判断 k、b 符号，比较函数值大小）、一次函数与方程 / 不等式的关系（如 “y=2x+1>0 时，x>-\frac {1}{2}$）、实际应用题。

二、8 年级数学高频难点及突破方法

1. 难点 1：几何证明题（步骤不规范，思路找不到）

• 突破方法：

1. “逆向推导” 找思路：比如要证明 “AB=CD”，先想 “怎么证线段相等？”→ 全等三角形对应边相等、等腰三角形两腰相等、平行四边形对边相等，再结合题目已知条件选方法（如已知 “AD∥BC，AD=BC”，可先证四边形 ABCD 是平行四边形，再得 AB=CD）；
2. 规范步骤写法：每一步推理都要写 “依据”（如 “∵AD∥BC（已知），∴∠A+∠B=180°（两直线平行，同旁内角互补）”），避免 “跳步”（比如直接写 “△ABC≌△DEF”，不写判定条件）；
3. 多练 “基础证明题”：先从课本例题、课后题入手，熟悉 “全等→平行四边形→矩形” 的证明逻辑，再挑战复杂题。

2. 难点 2：一次函数（图像与性质结合，应用题列解析式）

• 突破方法：

1. “数形结合” 理解性质：画一次函数图像（用两点法），直观感受 “k>0 上升，k<0 下降”“b 决定与 y 轴交点”，比如对比y=2x+3
2. （k=2>0，上升；b=3，交 y 轴 (0,3)）和y=−2x+3
3. （k=-2<0，下降；b=3，交 y 轴 (0,3)）的图像差异；
4. 列解析式 “抓两个量”：实际应用题中，先确定 “自变量 x”（如 “时间”“数量”）和 “因变量 y”（如 “路程”“利润”），再找两个 “x 和 y 的对应值”（如 “x=1 时 y=5，x=2 时 y=8”），代入y=kx+b
5. 列方程组求解；
6. 区分 “一次函数” 与 “正比例函数”：记住 “正比例函数是 b=0 的一次函数，图像过原点”，避免概念混淆。

3. 难点 3：因式分解（分解不彻底，公式用错）

• 突破方法：

1. 遵循 “先提公因式，再用公式” 的步骤：比如分解2x2
2. −8
3. ，先提公因式 2 得2(x2
4. −4)
5. ，再用平方差公式得2(x+2)(x−2)
6. ，避免直接用公式导致分解不彻底；
7. 熟记乘法公式的 “逆用形式”：平方差公式逆用：a2
8. −b2
9. =(a+b)(a−b)
10. ；完全平方公式逆用：a2
11. ±2ab+b2
12. =(a±b)2
13. ，遇到 “两项且符号相反” 优先想平方差，“三项” 优先想完全平方；
14. 验证结果：分解后用整式乘法还原，看是否与原式一致（如分解x2
15. +4x+4=(x+2)2
16. ，还原(x+2)2
17. =x2
18. +4x+4
19. ，正确）。